We, the round authors, are eternally grateful to all the brave who took part in this round. Sadly there were some issues to encounter, but we hope it only made the contest more interesting :)
Tutorial is loading...
Author — GreenGrape
Code: 33946912
Tutorial is loading...
Author — GreenGrape
Code: 33946939
Tutorial is loading...
Author — rek
Code (rek): 33953146
Code (xen): 33946949
Code (GreenGrape): 33947166
Tutorial is loading...
Author — GreenGrape
Code (xen): 33946962
Code (GreenGrape, solution 1): 33946974
Code (GreenGrape, solution 2): 33946993
Tutorial is loading...
Author — GreenGrape
Code (xen): 33947002
Code (GreenGrape): 33946911










The editorials had been very fast lately
Not as fast as my score's decline rate
That's sad man :'(
Great editorial! :)
Is there a term for binary numbers that fill in all 1's when xor'd? For example 11000 xor 00111 is 11111 so they fulfill this property.
I think if such numbers have a name problem B relies on this idea.
https://en.wikipedia.org/wiki/Ones%27_complement
I think it's just something like bitwise not. (maybe with specific width)
You're right, I made a stupid comment.
I can't believe B turned out to be so simple, I didn't realise it said "at most k"
I think you made a small mistake — the complexity in E is O((D(A) + D(B)) * log(D(A) + D(B)) * log1018)
I use two pointers so the complexity is true :) We are uploading the sample solutions now.
Can someone explain the calculation of f(x, y) in problem D?
Just apply all restrictions on both coordinates.
Can you explain it little more.
Let's solve it for a single x0. Imagine we're covered by a scoop located at x. What should be applied?
Combine them and solve the same problem for y. This will give you a rectangle where each point is valid.
Shouldn't x0 >= x ?
Oh, thanks for pointing out.
Can you elaborate on the next steps, i.e. how you solve these inequalities for x0 ?
Very nice problem set! I hope to see more contests from you in future.
For problem D, how do you check if a cell (x,y) has already been visited in O(1) ?
Make a set of pairs.
Oh okay I'm not really used to use sets that's why ^^ thanks
actually if you go by the solution , it's impossible to get a cell (x , y) two times,.. , but we still need to get the maximum cell at top so that's why we have to use heap or set , whatever you prefer , no worry about them getting repeated
the contest was very good for me, but i don't think that was a standard contest.
because normal Div.2 participants mostly solved problems A and B but in a standard contest, a normal participant usually solve 3 problems.
nevertheless thank you for the contest:)
Auto comment: topic has been updated by rek (previous revision, new revision, compare).
In problem E, how could I estimate |D(A)|? Should I just do what I guest and check it?
( In the contest, I think the size might went to 10^9 or larger, so I didn't try to implement and check it. TAT
BTW, I think it's a good contest, thank you!
Yep. It's a coding competition after all xD
Can you explain how did you come up with "sizes of both D(A) and D(B) do not exceed 106"?
I think we could just try to implement it and find it out
In problem D, how f(x, y) is formulated ?
That is "how many scoops cover this point".
For example, (2, 2) from sample case 1 (reference to the pic) has f(2, 2) = 4.
I mean, how it is generated?
f(x, y)= (max... — min...)*()
Take a look at this!
Do such thing with x0 and y0 separately and take their cartesian product.
Why isn't time limit for java 2x of C++ in codeforces, it is very painful to see same solutions running in C++ rather than in java, and this makes extremely difficult to pass solutions in java.
It's your choice if every contestant, what language to use. If you choose C++, you get good performance, but loose, for instance, BigInteger. If you want write all problems using same language, it's definitely your problems.
"Let N be our initial set. Sadly we cannot just generate D(N) since its size might be of the order of 8·10^^8". How did the you compute the number 8.10^^8 ?
Also, similarly, how did you come with the number O(log 10^^18 .(|Da| + |Db|)) ?
Thanks.
We cannot generate such a big set of numbers, so we are looking for a better way of computing the answer, and this way is described in the editorials.
But how did we approximate the size of this big set of numbers?
Use bruteforce to obtain those sets :)
Complexity to generate those sets using bruteforce ?
Can someone elaborate on the implementation details of the problem E?
Nevermind. I understood the implementation.
The first thought is to send the first elements to A and the rest to B. However, this is not enough; in this case the approximate size of D(A) might reach 7·106 which is way too much to pass.
How do we know this?
If you write a code to generate D(A) where A contains the first 8 prime numbers. You will see that its size will indeed be approximately 7e6. I have verified this on my computer.
What is the time complexity of the "count_le" function in xen's code?
It's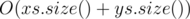 (or
(or 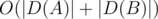 )
)
"The first thought is to send the first n / 2 elements to A and the rest to B. However, this is not enough".
I did exactly that and it passed in around 1100MS: http://codeforces.com/contest/912/submission/33953122
GreenGrape is that a typo, or did I get lucky?
That’s not a typo :)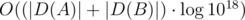
My solution uses two pointers approach and hence works in
Yours iterates through the smaller set and binary searches the greater, and hence works in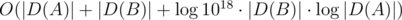
That means that a skew partition works fine in your case and fails in mine. As an opposite, the equallized partition slows down your solution and speeds up mine.
Got it..thanks :)
In problem C, isn't it easier just to add f(t) changes in map and then count ans after any change (choose max of them). And then output ans if f(t) == 0 after all changes or "-1" in another case. like this
For problem E: Can someone explain what's happening in the function "go" of the editorial solution? I understand that the primes are split between
lpandrp, but I didn't get what the recursive function calls will do:It generates all numbers less than 10^18 which can be written as product of primes in the desired set.
For example primes = {2,3}, you generate all numbers less than 10^18 which can be written in the form 2^k1 * 3^k2
What is the complexity to generate all such numbers in the "go" function ?
complexity per prime = log(1e18)/log(2) * log(1e18)/log(3) * log(1e18)/log(next prime in the sequence) *.... * log(1e18)/log(current prime)
here log has base 10.
But the interesting thing is, this is a very loose upper bound. So in practice it's not as bad as it looks.
thanks for a nice editorial :) specially D and E !
Can't E be solved using bitmask?
I thought of it too, but since the occurrence of each prime can be more than once, I decided against it..
I liked the thought behind E. It's all about optimizations!
some one interesting to problem B if you can choose "exactly" K numbers? obviously K=1 or 2 is like the ordinary problem
In problem " B " , in testcase #48 , n was 2^58,so answer should be 2^59-1(xorring 2^58 and 2^58 -1) but answer was 2^58-1 (when k=2)!! how!! also why different answers with log2() and log2l()... is it about (rounding off) of double value
2^58=1<<58=288230376151711744 testcase #48 is 288230376151711743 which is (2^58)-1 so...
oops!!xD
thanks....
but when i just used log2() instead of log2l() ,(int)(log2(n)+1) gave (59) and (int)(log2l(n)+1) gave 58!!why
both to me i have 59.. i dont know why you have 58 for (int)(log2l(288230376151711744)+1) UPD you can submit this to any problem
pls check your code for 288230376151711743 = (2^58-1) giving 58 ,59!!!!!
Really! its seem log2l work specially ,sor i dont kwow what log2l going on ,i usually use log2 instead maybe some "double" type problem ?
For problem D, May I ask why this part
|| (f_a == f_b && a > b);is added in the compare function of solution 2?(f_a == f_b && a > b)and(f_a == f_b && a < b)both give AC and without these output do not match.I wonder why?A set cannot contain equal elements by its definition. Hence if fa = fb, the second point will not be added.
In order to fix it we should force our set to treat them as distinct ones. Since all points are distinct, this comparison works fine.
In D we can use another method. Let see that optimal area is convex (or approach to convex). For this reason we should find rectangle area with square >=2*k. For find it let move vertical or gorizontal bounders (what's is better).
Yeah, but most such solutions fail somewhere between test cases 81 and 95.
It’s cool that yours passed.
in Tricky Alchemy problem,my algorithm was correct but in third test case, the output was correct but negative (-2147483648),i tried using long long,long double,int and it didn't work,any help?
Please add a link to your solution below.
"The first thought is to send the first elements to A and the rest to B. However, this is not enough; in this case the approximate size of D(A) might reach 7·106 which is way too much to pass. To speed it up we can, for example, comprise A of elements with even indexes (i.e p0, p2, ...) so that sizes of both A and B do not exceed 106 and the solution runs swiftly."
What's the difference? In both the case, one set will be of size floor(n/2), and the other will be of size n — floor(n/2). What am I missing?
Applied a minor correction, thank you. Should be up soon :)
done?
pls help me out of weirdity of log2() and log2l() behaviour towards (2^58-1) in problem b:(
Wonderful job with the editorial!!
So I've been stuck on E for a bit now (did this as a virtual contest and spent most of my time on it). I had a (I think) similar-ish idea. Instead of splitting the set in two I added one prime at a time, keeping track of the smallest k numbers one can make with the first m of the n primes. This (or at least my implementation of it) ended up being too slow. Is there a reason the DP approach is doomed to be too slow that I'm not seeing? Or is it likely just that my implementation sucks? Also (relatedly) I'm not seeing how to prove the O(|D(A)|+|D(B)|) part of the complexity? I suspect if someone would be nice enough to fill in this bit I'll see what I'm doing wrong on this problem.
k might be as large as 8·106.
GreenGrape , can you explain how do we get the numbers 8*10^8 (size of D(N) ) ... and also how do we get numbers 10^6 if we split N into A and B...
I think he found it out empirically . You can recursively compute the set A and B . It would be helpful if you try to think of it as a tree . At each height you can branch off into some power of the corresponding prime.
I'm currently stuck in a TLE while computing the the number of numbers less than a given number part . I tried Medo.'s idea. If someone has solved E in java and faced the same issue please help me out . CODE
I don't think it's possible to pass (logn)^2 in Java, at least without doing major changes to the generate function.
The solution in mashup takes 8190 seconds to run. The time limit is around 3.5 seconds, this looks like too much to optimize.
All Java solutions that passed run from 1.5 to 3.5 seconds, and they do it in logN. I don't think it would be possible to squeeze an extra log factor in.
The fastest solution in Java here runs in 1200MS : http://codeforces.com/contest/912/submission/33951400
Maybe you can use his generate function, and combine it with double binary search.
Note : I still find it surprisingly weird how can my CPP solution run in 1000MS without even attempting to optimize it while Java takes 8. I expected it to run in say 4-5 seconds at most.
I think that's due to using
ArrayList, I wrote another solution using arrays but even that gave a TLE though it ran ~3.3s on my PC . Actually generate and sort took ~0.8s only. Can you try running thisTakes 3.7 seconds, you are almost there. I think Java uses quick sort so that may slow it down (Changing long to Long to force merge sort takes 8) so try using your own sort function.
Thanks a lot , Finally AC
binarySearchand implemented my ownIn this Code (rek): 33953146 what does cnt[at-1]+=0 and cnt[time-1]+=0 do? why to do += by zero
That's a tricky (but not really beautiful in terms of code style) thing that lets us add a key (at-1 and time-1 respectively) to an STL C++ map. The "square brackets" operator of the map will create a key if it doesn't exist yet, so:
Why do we need to add this key at all? It's because both at-1 and time-1 are the last points of times when we can kill a certain enemy before its health gets changed to be too high to let us kill it.
Though I personally think that it's ugly as I mentioned before, it's short and efficient :)
Can someone explain C problem ? I couldn't understand the tutorial and why cnt[at]--?
at is the point where enemy's health becomes too high to kill it, so we have to decrease count of the people we can kill there by 1.
but intitially cnt[at]==0 ,right??
so it will get -1
cnt holds the difference between the previous and the current moments of time, so -1 would be ok, and mean that "the number of enemies we can kill now is less by 1".
Just by practicing E, I managed to understand how two pointers are more efficient than STL
upper_bound/lower_boundin merging results in sub-problems in a meet-in-the-middle problem. Never thinking that way before ;)Many thanks for enlightening me ;)
For Problem E, I used a Accepted code run the second sample. But I found a problem ==> I print the rank of 98 and rank of 93, both of them are 17, In other word both of them satisfy the Problem E, But the right answer is 93, so I want to know why it is right that if both of number have same rank, Always choose the smaller one. ( It can control by changeing the detail in the binary_search )
Hope someone can understand what I say and help me solve this problem, thanks!!!
I have a shorter(/est) solution for Problem B
For the second problem if we consider K=4 then we have chosen 2^p and 2^p - 1 that's all right but what about the other two numbers? How can you say that even including the other two numbers won't change the result?
Hi guys
B. New Year's Eve, can we do this using DP ???