Tutorial is loading...
Author: crvineeth97
Testers: deepanshugarg, nir123
Author's code
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long ans=LLONG_MIN, n, x;
cin>>n;
for (long long i = 0; i < n; i++)
{
cin>>x;
for (long long j = 0; j*j<=x; j++)
if (j*j == x)
x = LLONG_MIN;
ans = max(ans, x);
}
cout << ans << endl;
return 0;
}
Tutorial is loading...
Author: RohanRTiwari
Tester: Superty
Author's code
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int cnt[100005];
int main() {
ios::sync_with_stdio(false);
int n;
cin >> n;
while(n--) {
int x;
cin >> x;
cnt[x]++;
}
for (int i = 1; i <= 1e5; i++) {
if (cnt[i] % 2 == 1) {
cout << "Conan\n";
return 0;
}
}
cout << "Agasa\n";
return 0;
}
Tutorial is loading...
Author: aman_shahi2
Tester: mprocks
Author's code
#include <bits/stdc++.h>
using namespace std;
#define MOD 1000000007
int dp[1004];
long long ncr[1004][1004];
int ones(int n)
{
int cnt = 0;
while(n)
{
if(n%2 == 1)
{
cnt++;
}
n /= 2;
}
return cnt;
}
void calcncr()
{
for(int i = 0; i <= 1000; i++)
{
ncr[i][0] = 1;
}
for(int i = 1; i <= 1000; i++)
{
for(int j = 1; j <= 1000; j++)
{
ncr[i][j] = (ncr[i-1][j-1] + ncr[i-1][j])%MOD;
}
}
}
int main()
{
string n;
int k;
calcncr();
dp[1] = 0;
for(int i = 2; i <= 1000; i++)
{
dp[i] = dp[ones(i)] + 1;
}
cin >> n >> k;
if(k == 0)
{
cout << "1\n";
return 0;
}
long long nones = 0, ans = 0;
for(int i = 0; i < n.size(); i++)
{
if(n[i] == '0')
{
continue;
}
for(int j = max(nones, 1LL); j < 1000; j++)
{
if(dp[j] == k-1)
{
ans = (ans + ncr[n.size()-i-1][j-nones])%MOD;
if(i == 0 && k == 1)
{
ans = (ans+MOD-1)%MOD;
}
}
}
nones++;
}
int cnt = 0;
for(int i = 0; i < n.size(); i++)
{
if(n[i] == '1')
{
cnt++;
}
}
if(dp[cnt] == k-1)
{
ans = (ans + 1)%MOD;
}
cout << ans << endl;
return 0;
}
Tutorial is loading...
Author: RohanRTiwari
Testers: codelegend, Superty
Author's code
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int tree[2000000];
int trstp = 1;
int gcd(int x, int y) {
return y == 0 ? x : gcd(y, x % y);
}
void query(int root, int u, int v, int x, int s, int e, int& ans) {
if (e < s || v < u || e < u || v < s) {
return;
} else if (u <= s && e <= v) {
if (tree[root] % x == 0) {
return;
} else {
while (root < trstp) {
if (tree[2*root] % x != 0) {
if (tree[2*root + 1] % x != 0) {
ans += 2;
return;
}
root = 2*root;
} else {
root = 2*root + 1;
}
}
ans++;
return;
}
}
int mid = (s + e)/2;
query(2*root, u, v, x, s, mid, ans);
if (ans > 1) {
return;
}
query(2*root + 1, u, v, x, mid + 1, e, ans);
}
void update(int p, int x) {
p += trstp - 1;
tree[p] = x;
p /= 2;
while (p > 0) {
tree[p] = gcd(tree[2*p], tree[2*p + 1]);
p /= 2;
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int n;
cin >> n;
while (trstp < n) {
trstp *= 2;
}
for (int i = trstp; i < trstp + n; i++) {
cin >> tree[i];
}
for (int i = trstp - 1; i >= 1; i--) {
tree[i] = gcd(tree[2*i], tree[2*i + 1]);
}
int q;
cin >> q;
while (q--) {
int t;
cin >> t;
if (t == 1) {
int l, r;
int x;
cin >> l >> r >> x;
int ans = 0;
query(1, l, r, x, 1, trstp, ans);
cout << (ans <= 1 ? "YES\n" : "NO\n");
} else {
int i;
int y;
cin >> i >> y;
update(i, y);
}
}
return 0;
}
Tutorial is loading...
Author: born2rule
Testers: devanshg27, FundamentalEq
Author's code
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define ll long long
#define db long double
#define ii pair<int,int>
#define vi vector<int>
#define fi first
#define se second
#define sz(a) (int)(a).size()
#define all(a) (a).begin(),(a).end()
#define pb emplace_back
#define mp make_pair
#define FN(i, n) for (int i = 0; i < (int)(n); ++i)
#define FEN(i,n) for (int i = 1;i <= (int)(n); ++i)
#define rep(i,a,b) for(int i=a;i<b;i++)
#define repv(i,a,b) for(int i=b-1;i>=a;i--)
#define SET(A, val) memset(A, val, sizeof(A))
typedef tree<int ,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update>ordered_set ;
// order_of_key (val): returns the no. of values less than val
// find_by_order (k): returns the kth largest element.(0-based)
#define TRACE
#ifdef TRACE
#define trace(...) __f(#__VA_ARGS__, __VA_ARGS__)
template <typename Arg1>
void __f(const char* name, Arg1&& arg1){
cerr << name << " : " << arg1 << std::endl;
}
template <typename Arg1, typename... Args>
void __f(const char* names, Arg1&& arg1, Args&&... args){
const char* comma = strchr(names + 1, ','); cerr.write(names, comma - names) << " : " << arg1<<" | ";__f(comma+1, args...);
}
#else
#define trace(...)
#endif
const int L=200005,N=(1<<20);
//call dfsMCT,change solve and dfs1
vi vpart[L],ad[L]; bool vis[L];//par:parent in cent|H:depth
int SZ[L],par[L],part[L],H[L],cpart;//cpart:no of parts in cent
ll ans[L],dp[L];
string s;
int dfsSZ(int u,int p=-1)
{
SZ[u]=1;//vpart[i]:nodes in part i
for(int v:ad[u])
if(!vis[v] && v!=p)
SZ[u]+=dfsSZ(v,u);
return SZ[u];
}
int dfsFC(int u,int r,int p=-1)
{
for(int v:ad[u])
if(!vis[v] && v!=p)
{
if(SZ[v]>SZ[r]/2)
return dfsFC(v,r,u);
}
return u;
}
int cnt[N],val[L],tmp[N];
void dfs1(int u,int r,int p=-1)
{
dp[u]=0;
if(p==r)
{
part[u]=++cpart;
vpart[cpart].clear();
}
else if(p!=-1) part[u]=part[p];
if(p!=-1) vpart[cpart].pb(u);
for(int v1:ad[u])
if(!vis[v1]&&v1!=p)
{
H[v1]=H[u]+1;
val[v1]=(val[u]^(1<<(s[v1-1]-'a')));
dfs1(v1,r,u);
}
}
void dfs2(int u,int r,int par=-1)
{
dp[u]=cnt[val[u]];
rep(i,0,20)
dp[u]+=cnt[val[u]^(1<<i)];
for(int v1:ad[u])
{
if(vis[v1] || v1==par) continue;
dfs2(v1,r,u);
dp[u]+=dp[v1];
}
ans[u]+=dp[u];
}
void solve(int r,int szr)
{
H[r]=cpart=0;
val[r]=(1<<(s[r-1]-'a'));
dfs1(r,r);
rep(i,1,cpart+1)
for(int v1:vpart[i])
cnt[val[v1]]++;
cnt[val[r]]++;
rep(i,1,cpart+1)
{
for(int v1:vpart[i])
{
cnt[val[v1]]--;
val[v1]^=(1<<(s[r-1]-'a'));
tmp[val[v1]]++;
}
for(int v1:vpart[i])
{
if(tmp[val[v1]])
{
dp[r]+=(ll)tmp[val[v1]]*cnt[val[v1]];
rep(j,0,20)
dp[r]+=(ll)tmp[val[v1]]*cnt[val[v1]^(1<<j)];
tmp[val[v1]]=0;
}
}
dfs2(vpart[i][0],r,r);
for(int v1:vpart[i])
{
val[v1]^=(1<<(s[r-1]-'a'));
cnt[val[v1]]++;
}
}
cnt[val[r]]--;
dp[r]+=cnt[0];
rep(i,0,20)
dp[r]+=cnt[(1<<i)];
ans[r]+=dp[r]/2;
rep(i,1,cpart+1)
for(int v1:vpart[i]) cnt[val[v1]]--;
}
void dfsMCT(int u,int p=-1)
{
dfsSZ(u);
int r=dfsFC(u,u);
par[r]=p; solve(r,SZ[u]); vis[r]=true;
for(int v:ad[r])
if(!vis[v]) dfsMCT(v,r);
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(NULL) ; cout.tie(NULL) ;
int n,x,y;
cin>>n;
rep(i,1,n)
{
cin>>x>>y;
ad[x].pb(y); ad[y].pb(x);
}
cin>>s;
dfsMCT(1);
rep(i,1,n+1) cout<<ans[i]+1<<" ";
cout<<endl;
return 0 ;
}
Tutorial is loading...
There was an unexpected solution that involved bitset that runs in complexity O(N2 / 32). Have a look at Syloviaely 's code: 34364964
Author: RohanRTiwari
Testers: born2rule, devanshg27, additya1998, virus_1010, nir123
Author's code
#include <bits/stdc++.h>
#define fr(x) scanf("%d", &x)
#define SQRN 150
using namespace std;
const int sa = 2 * SQRN + 10;
const int LEN = 100010;
char s[LEN], sq[LEN], zstring[2*LEN];
int z[2*LEN];
string temps;
struct SuffixAutomaton {
int edges[26][sa], link[sa], length[sa], isTerminal[sa], dp1[sa], last;
int sz;
SuffixAutomaton() {
last = 0;
sz = 0;
}
void set(int k) {
for(int i = 0; i < 26; ++i) edges[i][k] = -1;
}
void build(string &s) {
link[0] = -1;
length[0] = 0;
last = 0;
sz = 1;
set(0);
for(int i=0;i<s.size();i++) {
set(sz);
length[sz] = i+1;
link[sz] = 0;
int r = sz;
++sz;
int p = last;
while(p >= 0 && edges[s[i]-'a'][p] == -1) {
edges[s[i] - 'a'][p] = r;
p = link[p];
}
if(p != -1) {
int q = edges[s[i] - 'a'][p];
if(length[p] + 1 == length[q]) {
link[r] = q;
} else {
for(int i = 0; i < 26; ++i) {
edges[i][sz] = edges[i][q];
}
length[sz] = length[p] + 1;
link[sz] = link[q];
int qq = sz;
++sz;
link[q] = qq;
link[r] = qq;
while(p >= 0 && edges[s[i] - 'a'][p] == q) {
edges[s[i] - 'a'][p] = qq;
p = link[p];
}
}
}
last = r;
}
for(int i = 0; i < sz; ++i) isTerminal[i] = 0, dp1[i] = -1;
int p = last;
while(p > 0) {
isTerminal[p] = 1;
p = link[p];
}
}
int solve(int pos) {
if(dp1[pos] != -1) return dp1[pos];
dp1[pos] = isTerminal[pos];
for(int i=0; i<26; ++i){
if(edges[i][pos] != -1) dp1[pos] += solve(edges[i][pos]);
}
return dp1[pos];
}
int run() {
int cur = 0;
for(int i=1; sq[i] != '\0'; ++i) {
auto it = edges[sq[i] - 'a'][cur];
if(it == -1) return 0;
else cur = it;
}
return solve(cur);
}
} SA[800];
void computeZ() {
int l, r;
z[0] = 0;
l = r = -1;
for(int i=1; zstring[i] != '\0'; ++i) {
z[i]=0;
if(r>i) {
z[i]=min(z[i-l], r-i+1);
}
while(zstring[i+z[i]] == zstring[z[i]]) ++z[i];
if(i+z[i]-1 > r) {
r = i+z[i]-1;
l = i;
}
}
}
int computeBrute(int l, int r, int sqlen) {
int zslen = 0, ans = 0;
for(int i=1; i<=sqlen; ++i) {
zstring[zslen++] = sq[i];
}
zstring[zslen++] = '$';
for(int i=l; i<=r; ++i) {
zstring[zslen++] = s[i];
}
zstring[zslen] = '\0';
computeZ();
for(int i=1; i<zslen; ++i) {
if(z[i] >= sqlen) {
++ans;
}
}
return ans;
}
int main() {
int q, typ, l, r, slen;
char ch;
scanf(" %s", &s[1]);
slen = strlen(&s[1]);
fr(q);
for(int i=0; i<=slen; i+=SQRN) {
temps = "";
int tempr = min(i+SQRN-1, slen);
for(int j=max(1, i); j<=tempr; ++j) {
temps += s[j];
}
SA[i/SQRN].build(temps);
}
while(q--) {
fr(typ);
if(typ == 1) {
scanf("%d %c", &l, &ch);
s[l] = ch;
temps = "";
int bkt = l/SQRN;
int tempr = min(slen, (bkt+1)*SQRN-1);
for(int i=max(1,bkt*SQRN); i<=tempr; ++i) {
temps += s[i];
}
SA[bkt].build(temps);
}
else {
scanf("%d %d %s", &l, &r, &sq[1]);
int sqlen = strlen(&sq[1]);
if(sqlen >= SQRN || r-l <= 2*SQRN) {
printf("%d\n", computeBrute(l, r, sqlen));
}
else {
int lbkt = l/SQRN, rbkt = r/SQRN, ans = 0;
for(int i=lbkt+1; i<rbkt; ++i) {
ans += SA[i].run();
}
ans += computeBrute(l, (lbkt+1)*SQRN-1, sqlen);
ans += computeBrute(rbkt*SQRN, r, sqlen);
for(int i=lbkt+1; i<=rbkt; ++i) {
ans += computeBrute(max(l, i*SQRN - sqlen + 1), min(r, i*SQRN + sqlen - 2), sqlen);
}
printf("%d\n", ans);
}
}
}
return 0;
}
Tutorial is loading...
Author: FundamentalEq
Tester: born2rule
Author's code
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define ll long long
#define db long double
#define ii pair<int,int>
#define vi vector<int>
#define fi first
#define se second
#define sz(a) (int)(a).size()
#define all(a) (a).begin(),(a).end()
#define pb push_back
#define mp make_pair
#define FN(i, n) for (int i = 0; i < (int)(n); ++i)
#define FEN(i,n) for (int i = 1;i <= (int)(n); ++i)
#define rep(i,a,b) for(int i=a;i<b;i++)
#define repv(i,a,b) for(int i=b-1;i>=a;i--)
#define SET(A, val) memset(A, val, sizeof(A))
typedef tree<int ,null_type,less<int>,rb_tree_tag,tree_order_statistics_node_update>ordered_set ;
// order_of_key (val): returns the no. of values less than val
// find_by_order (k): returns the kth largest element.(0-based)
#define TRACE
#ifdef TRACE
#define trace(...) __f(#__VA_ARGS__, __VA_ARGS__)
template <typename Arg1>
void __f(const char* name, Arg1&& arg1){
cerr << name << " : " << arg1 << std::endl;
}
template <typename Arg1, typename... Args>
void __f(const char* names, Arg1&& arg1, Args&&... args){
const char* comma = strchr(names + 1, ','); cerr.write(names, comma - names) << " : " << arg1<<" | ";__f(comma+1, args...);
}
#else
#define trace(...)
#endif
const int L = 17 ;
const int L2 = 1<<L ;
const int mod = 1e9+7 ;
int sbits[L2] ;
vi oddbits ;
inline int add(int x,int y)
{
x+=y;
if(x>=mod) x-=mod;
if(x<0) x+=mod;
return x;
}
inline int mult(int x,int y)
{
ll tmp=(ll)x*y;
if(tmp>=mod) tmp%=mod;
return tmp;
}
inline int pwmod(int x,int y)
{
int ans=1;
while(y){if(y&1)ans=mult(ans,x);y>>=1;x=mult(x,x);}
return ans;
}
vector<ii> nus[L] ;
void zeta(int A[L2])
{
FN(i,L)
{
for(ii m:nus[i]) A[m.fi]=add(A[m.fi],A[m.se]) ;
}
}
void meu(int A[L2])
{
for(int i:oddbits) A[i] = mod - A[i] ;
zeta(A) ;
for(int i:oddbits) A[i] = mod - A[i] ;
}
void conv(int A[L2],int B[L2])
{
zeta(A), zeta(B);//return
FN(i,L2) A[i]=mult(A[i],B[i]);
meu(A);
}
int t[L+1][L2],t1[L2] ;
void subsetconv(int A[L2],int ans[L2])
{
FN(i,L2) t[sbits[i]][i] = A[i] ;
FN(i,L+1) zeta(t[i]) ;
FN(c,L+1) FN(a,c+1)
{
int *t2 = t[a], *t3 = t[c-a] ;
FN(i,L2) t1[i]=mult(t2[i],t3[i]) ;
meu(t1) ;
FN(i,L2) if(sbits[i] == c) ans[i]=add(ans[i],t1[i]) ;
}
}
vector<ii> su[L] ;
void transform(int p[L2],bool inv=false){ int u,v;
for(int len=1,l=2;l<=L2;len<<=1,l<<=1)for(int
i=0;i<L2;i+=l) FN(j,len){
u=p[i+j],v=p[i+j+len] ;
if(inv) {p[i+j]=add(u,v),p[i+j+len]=add(u,-v);}
else {p[i+j]=add(u,v),p[i+j+len]=add(u,-v);}}
if(inv){int d=pwmod(L2,mod-2);FN(i,L2)p[i]=mult(p[i],d);} }
int cnt[L2],fib[L2],A[L2],B[L2],C[L2],a[L2],b[L2],c[L2] ;
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(NULL) ; cout.tie(NULL) ;
FN(i,L2)
{
sbits[i] = __builtin_popcount(i) ;
if(sbits[i] & 1) oddbits.emplace_back(i) ;
FN(j,L)
{
if(i&(1<<j)) nus[j].emplace_back(mp(i,i^(1<<j))) ;
if((i&(1<<j)) == 0) su[j].emplace_back(mp(i,i^(1<<j))) ;
}
}
FN(i,L) reverse(all(su[i])) ;
fib[1] = 1 ; rep(i,2,L2) fib[i] = add(fib[i-1],fib[i-2]) ;
int N,x ; cin>>N ;
FN(i,N)
{
cin>>x, ++cnt[x] ;
}
subsetconv(cnt,A) ;
FN(i,L2) A[i]=mult(A[i],fib[i]) ;
FN(i,L2) B[i]=mult(cnt[i],fib[i]);
FN(i,L2) C[i]=cnt[i] ;
transform(C) ;
FN(i,L2) C[i]=mult(C[i],C[i]) ;
transform(C,1) ;
FN(i,L2) C[i]=mult(C[i],fib[i]) ;
int ans = 0 ;
FN(p,L)
{
FN(i,L2) a[i]=b[i]=c[i]=0 ;
for(ii m:nus[p]) a[m.se]=A[m.fi],b[m.se]=B[m.fi],c[m.se]=C[m.fi] ;
FN(i,L)
{
for(ii m:su[i])
{
a[m.fi]=add(a[m.fi],a[m.se]) ;
b[m.fi]=add(b[m.fi],b[m.se]) ;
c[m.fi]=add(c[m.fi],c[m.se]) ;
}
}
FN(i,L2) a[i]=mult(a[i],mult(b[i],c[i])) ;
meu(a) ;
ans = add(ans,a[(1<<L)-1]) ;
}
ans = ans == 0 ? 0 : mod - ans ;
cout << ans << "\n" ;
return 0 ;
}
Tutorial is loading...
Author: Superty
Tester: codelegend
Author's code
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll mod;
const int maxn = 2e2 + 2;
ll tree[maxn][maxn][maxn];
ll c[maxn][maxn];
int main() {
ios::sync_with_stdio(false);
int n, d;
cin >> n >> d >> mod;
c[0][0] = 1;
for (int i = 1; i <= n; i++) {
c[i][0] = 1;
for (int j = 1; j <= i; j++) {
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
}
tree[1][1][0] = 1;
for (int i = 1; i < n; i++) { // adding trees of size i
for (int j = 1; j <= n; j++) {
for (int k = 0; k <= d; k++) {
tree[i + 1][j][k] = tree[i][j][k];
}
}
ll tree_i = 0;
for (int j = 0; j < d; j++) {
tree_i = (tree_i + tree[i][i][j]) % mod;
}
ll ways = 1;
for (int j = 1; i*j <= n && j <= d; j++) { // adding j such trees
ways = (ways * c[i*j - 1][i - 1]) % mod; // ((ij)! tree[i]^(j-1))/(i!^j j!)
for (int k = 1; k + i*j <= n; k++) { // adding to trees of size k
ll cc = (ways * c[k + i*j - 1][k - 1]) % mod;
for (int deg = 0; deg + j <= d; deg++) {
tree[i + 1][k + i*j][deg + j] = (tree[i + 1][k + i*j][deg + j] + cc*((tree[i][k][deg]*tree_i) % mod)) % mod;
}
}
ways = (ways * tree_i) % mod;
}
}
ll total_trees = 0;
for (int i = 0; i <= n - 1; i++) { // there are i vertices lying on paths increasing from the root
for (int j = 0; j <= d; j++) {
for (int k = 0; j + k <= d; k++) {
if (k == 1) {
continue;
}
total_trees = (total_trees + ((tree[n][i + 1][j]*tree[n][n - i][k]) % mod)) % mod;
}
}
}
cout << (2*((n*(n-1)) % mod)*total_trees) % mod << '\n';
return 0;
}











Afaik subset sum convolution takes O(2n * n2) time , so shouldn't the complexity for G be 217 * 172? Anyways since 317 is pretty small here , we can just use that.
I don't know a way to do this using 2n·n2 even though I was acquainted with this problem, however I was aware of 2n·n3 solution. Can you elaborate on that?
For problem, in my code, function "subset_pow_convol" is O(Nlog(N)2 + Nlog(N)2logK) (it theoretically can reduce to O(Nlog(N)2 + Nlog(N)log(log(N))logK)). Here, we take K = 2.
I googled the algorithm and the first link gives 2nn2 algorithm: Fourier Meets Mobius: Fast Subset Convolution. Do you inverse n2 products separately before adding them up?
Thank, that's indeed tricky to compute n forward transformations, multiply them and add accordingly and compute one backward transformation instead of using convolutions as blackboxes.
All the above links seem overly complicated to me so i will just describe my approach which doesn't involve any fourier transforms.
To calculate A*B , calculate FA[i][j] = A[j] if bitcount(j) = i else 0 , similarly calculate FB , now do sum over subset dp over this to have FA[i][j] = sum of FA[i][k] where k is subset of j bitcount(k) = i , do the same on FB , now calculate FC[i][j] = FA[0][j] * FB[i][j] + FA[1][j] * FB[i-1][j] + ... FA[i][j] * FB[0][j] , now FC[i][j] not only consists of relevant product from A and B but there is some overlapping , but the overlapping must have been counted in proper subsets of j hence we can do inverse sum over subsets dp to subtract them.
That's exactly how I imagined this :). But it's good to have it clearly written here, so that maybe useful for others as well.
Can anyone explain the solution for C in brief. What does the precomputated DP array actually store ???
dp[k] stores the number of steps it takes k to reduce to 1. For instance, dp[1] = 0 and dp[13] = 3.
what about the ncr array?? can you explain me the whole solution. i am not geting it at all.-
Sure. I won't be able to do it completely in depth, but I can try my best. The dp array can be calculated like this: set dp[1] = 0. for(int i = 2; i <= 1000; i++) dp[i] = 1 + dp[__builtin_popcount(i)]; __builtin_popcount(i) just gives the number of 1 bits in i
ncr is also sort of a dp array. It stands for the mathematical combination function. C(n, r) = n! / ((n — r)! * r!). There is a special property that C(n, r) = C(n — 1, r) + C(n — 1, r — 1), called Pascal's identity. So, you can set ncr[i][0] = 1 and ncr[i][i] = 1 for all values of i up to 1000. Then, you can iterate through and set ncr[i][j] = ncr[i — 1][j] + ncr[i — 1][j — 1]. (Also, this n is not the n from the problem) If you don't know what the combination function does, it tells you the number of ways to choose a subset of r elements from a total of n. Note that 0 <= r <= n. https://en.wikipedia.org/wiki/Combination might also help
Of course, all this while, you are doing calculation mod 1000000007.
The reason we are choosing to have dp be size 1000 is because the value of n that we are given in the problem has at most 1000 1 bits. So, what we can do is iterate through the dp array. Whenevery dp[i] == k — 1, we can calculate the number of numbers <= n that have i one bits. In other words, we want the number of numbers no larger than n that reduce to i in one operation.
The method to calculate this number is described in the editorial.
thnx a lot. understood most of the part now. :-)
Thanx. I really did not know about Pascal's identity. Thanx a lot.
Hello , thanks for your explanation . could you please explain the solve function in more details http://codeforces.com/contest/914/submission/34369389
Thanks
Okay, here I go trying to explain the solve function. First of all, what does it do? solve(numSet, currBit) gives the number of numbers <= n such that
1) all the bits up to but not including the currBit-th bit (0 — indexing) in n match up
2) there are exactly numSet one bits from the currBit-th bit onwards (inclusive).
So this is what each line does:
if(numset < 0) return 0;
Obviously, you cannot achieve a negative number of one bits, so the answer in this case is 0.
if(currBit == n.size()) return ((numset == 0) ? 1 : 0);
If you hae gone through every single bit, you either return 1 if you need exactly 0 more one bits, or 0 otherwise since there is no more room for more one bits.
ll res = 0; if(n[currBit] == '1') res += C(n.size() — currBit — 1, numset);
Notice here that C(A, B) is the one described in my earlier post. It tells you the number of ways to choose B things from a total of A. Here, we say, if the current bit of n is a one bit, we can set our bit to 0 and then from here on out, the bits can be anything we want. So, out of the remainin n.size() — currBit — 1 bits, we can choose any subset of them with size numSet to be our one bits.
res += solve(numset — ((n[currBit] == '1') ? 1 : 0), currBit + 1);
Here, we set out current bit to whatever the current bit of n is, and then recursively solve the problem.
could someone please explain what is "subset convolution"?
First of all, I have just learnt about those, so please correct me if I said something wrong.
If you are asking just about subset convolution, you can find definition and good algorithm for it in this book (page 125 in the book — page 133 in the pdf):
https://link.springer.com/content/pdf/10.1007%2F978-3-642-16533-7.pdf
UPD: I think this is better resource: http://home.iitk.ac.in/~gsahil/cs498a/report.pdf
I will give a simple idea with an easy but slow algorithm for it:
You have a Set U of n elements, and you have 2 functions f(x) and g(x) which takes subset of U as an input, and you want to produce third function:
(f*g)(S) = sum (f(X)*g(Y)) for all X,Y such that X and Y are subsets of S and they are disjoint and their union is S
imagine that subset is represented as mask of n bits:
so 101 represents subset S = {first element of U, third element of U}
so (f*g)(101) = f(101) * g(000) + f(100) * g(001) + f(001) * g(100) + f(000) * g(101)
An easy algorithm for it is to iterate over all masks (S), then iterate over its submasks (X), if you have S and X, you can easily get Y, this run in complexity O(3^n)
Code:
in problem G: if you considered n=17 and f(x) = g(x) = count(x),
running convolution on those functions will get what is stated in the tutorial.
-------------------------
I will share other useful links about convolutions (not subset convolution):
This tutorial explains XOR convolution using transformation:
https://apps.topcoder.com/wiki/display/tc/SRM+518
XOR, OR and AND transformations can also be done using karatsuba-like approach in nlogn (where n is number of elements),
For XOR convolution nlogn karatsuba-like approach, see rng_58 post:
https://apps.topcoder.com/forums/?module=Thread&threadID=720792&start=0
For AND convolution nlogn karatsuba-like approach, see triveni solution:
http://codeforces.com/contest/914/submission/34392096
OR convolution nlogn karatsuba-like approach is similar to AND one.
Hope this help :)
Thank you very much!
Hey, I don't understand why my solution for problem D gets TLE. I think the time limit was really tight, but it shouldn't give TLE: http://codeforces.com/contest/914/submission/34387847
It should get TLE, this is n log^3 n, because gcd is a log factor. Put the bsearch into the tree and it will remove a log factor
In H, I think
tree[i][j]can be calculated in O(n3) if you enumerate the size of subtree of the child which has the minimum index during the transition.BTW, such a weak sample input makes me confused. I think it will be much better if you add a larger sample or give a more detailed explanation about the modification Ember could do (I think this process is a little bit complex and is somehow hard for me to understand well).
Yes, I think you're right. Nice.
I wasn't sure how to improve the sample case without giving away the game. Yes, we should've given a more detailed explanation.
I see many Div2D solutions having complexity O(q*logn*logn) failed. My solution also had same complexity and is wrong!
Code
Looks like I was too lucky yesterday night! :)
I had the same solution for C . Missed the k = 1 Case :( . I did it using simple meimoization and not using binomial coefficients http://codeforces.com/contest/914/submission/34399092
Why at yesterday's contest problem C if k==0 the answer is one ?
For k == 0 there is only one number which will be always less than or equal to any given n . That number is 1
i couldn't understand the problem is how many numbers less than or equal to n after k operations will be reduced to one right ?
Yes. But you have to find minimum operations. If n == 1 then minimum operations would be 0 coz it's already 1 .But for any other number at least 1 operation would be required.So for k==0 there is only one number
Not only did I fail the k==1 case, but I also unsuccessfully hacked solutions cause I thought their k==1 case was bugged :)
Can someone explain what the mask[u] is in E? Are we taking the path from the centroid to u? Does it matter if the paths of u and v intersect or does the solution only consider when u and v are in different parts?
mask[u] has cnt[j]%2 at jth bit in binary representation of mask[u], considering characters from root to u. Now when we root the tree at centroid, we consider the paths from root to subtree of u and from subtree of u to vertices in other parts when we calculate answer for u. We do this for each centroid.
10
30757 30757 33046 41744 39918 39914 41744 39914 33046 33046
how the ans for this will be Conan .. plzz expalain
Sorted input: 30757 30757 33046 33046 33046 39914 39914 39918 41744 41744
Conan takes 39918
Agasa takes 41744
Conan takes 41744
he must choose LARGEST CARD in order to delete max no of cards so he can ensure its winning .But why u choose 2 largest card why not 41744 IN turn of conan .. by ur case he is not PLAYING OPTIMALLY expalin me i'm confused
It is not optimal to remove as many cards as possible.
It is optimal to play in such a way that you win. This winning strategy is explained in the editorial.
what a great editorial mate :)
I have two questions regarding the PROBLEM — C
1-- Since the number of set bits in numbers smaller than
2^1000 is less than 1000, any number smaller than 2^1000 would reduce to a number less than 1000 in one step. Can u give me a valid proof for this using an example
2-- How do u assume that the min no of steps req to convert a no in to 1 is equal to the order of that no and what role order signifies here.
A number less than 21000 has at most 1000 digits in binary, so it can have at most 1000 digits set to 1.
We are defining order here.
In C We can iterate through all possible i and compute the answer using binomial coefficients.How?
Check the code for clarification. For a given i (as defined in the statement) the number of possibilities for indices i + 1 to n to have k ones is n - i choose k.
I had understood that but can't understand the logic behind it...Can you please explain?
Got it.
Can somebody tell me what's wrong with my code for Problem C. I can't figure it out. My Solution
Can someone explain why this code fragment is used? if(i == 0 && k == 1) ans = (ans+MOD-1)%MOD
in Problem C, why do we use Binomial co-efficients? and what is the logic of this line?
Every number x < n satisfies the property that, for some i (1 ≤ i < k), the first i - 1 digits of x are the same as that of n, the ith digit of n is 1, and the i-th digit of x is 0. We can iterate through all possible i and compute the answer using binomial coefficients, that can be computed in O(l) where l is the length of binary representation of n.
Please explain
One more alternate solution for problem F :
Note that there is lot of optimization needed to get it through. Here is my submission 34404651, if anyone is interested. Note that unordered map won't work, I had to implement simple hash table. Also many dirty optimizations like, unsigned short int etcetera.
http://codeforces.com/contest/914/submission/34377829
Looks like O(n3 / 32). Does it pass only because of weak tests?
It's O(N2). Let K=lengh of queries, each query is O(NK) for K>12, and O(N) otherwise, and we have N/K queries
You right.
Can someone tell, what is wrong in my iterative segment tree solution of D 34410510
I have one doubt in problem C. Question is asking about numbers which can be reduced to 1 in minimum k steps. then shouldn't we have to compute for all dp[i]>=k-1 ? Here we are calculating for the numbers that will be reduced to 1 in exactly k steps. Correct me if I am wrong or have misunderstood something. Thanks.
From what I can understand from your comment, I think you are a bit confused between the terms "minimum" and "at least". Please note that after reaching 1, the added number of operations that you will do will be redundant and thus won't fit into the category of "minimum". Thus we will be picking elements from the dp[] which are exactly equal to k-1 and not such that dp[i]>=k-1. I hope this helps.
Thanks.I understood now.
can anyone explain problem c in simple layman's term. unable to understand second test
The number of steps to reduce a number x is entirely determined by the number of 1 in its binary representation. Let f be the function f(x) = number of 1 in its representation
Compute in table d recursively the number of steps required to reach 1 from every number from [1,1000]. d[i]=d[f(i)]
Then go through this table, for each of the values i so that d[i] is equal to k, you need to add the number Z(n,i) of numbers not greater than n that have i 1 in their representation. As a special case, you'll have to remove 1 from this number if k==1, because of the fact that 1 becomes 1 in 0 steps. let p be the number of digits of the binary representation of n.
You already know that there are C(p,i) ways to make a number lower than 2^p with i 1. C is the combination function. You'll need these values for p<=1000 you can compute these recursively.
Let Y(n,p,i) be the number of number greater than n, but with no more than p in its binary representation that have i 1 in their representation. Thus Z(n,i)=C(p,i)-Y(n,p,i)
Thus if you compute Y(n,p,i), you win !
You can compute Y(n,p,i) recursively on p. by using the digits of the representation of n.
If the first digit of n is 1, Y(n,p,i)=Y(n',p-1,i-1) where n' is n with the first digit removed. That is because no number starting with 0 is greater than n.
If the first digit of n is 0, Y(n,p,i)=C(p-1,i-1)+Y(n',p-1,i) This is because all numbers starting with 1 will be greater than n (there are C(p-1,i-1) cause the first one is already placed and you got p-1 slots remaining for i-1 "1" digits).
You can also stop as soon as the second argument becomes lower than the third argument, cause in that case Y is worth zero.
Then you can output the sum of Z(n,i) (or as stated above Z(n,1)-1 if k==1)
Are you sure it is k instead of i in Y(n,p,i)=C(p-1,k-1)+Y(n',p,i) ?
Thanks you were correct, I tried to fix my mistakes.
Thanks for fixing but please replace all the remaining k's below this line
"If the first digit of n is 0, Y(n,p,i)=C(p-1,i-1)+Y(n',p-1,i) This is because all numbers starting with 1 will be greater than n"
in your post with i so that it is clear for others who will read the post.
can you take a example small one other than given test cases and 'k' , i ,mean a binary of 'n' and 'k'. and solve it according the statement you have above written.it would be easy to grasp your logic.
OK :
110001 3
I create recursively a value of the number of steps taken to reach 1 depending on the number of "1" bit in the initial binary representation. I find that all the numbers that have 3,5 or 6 "1" initially will work, i.e. give 3 steps to reach 0. I will go through these cases :
The logic : it's easier to remove numbers too big rather than to count all numbers below a certain threshold cause it enables a closed form formula (the combinations). if your threshold starts with a 0, you disqualify all numbers that start with a 1 and have the correct number of 1 (they are all higher than your threshold, and you got a closed formula),
Then you need to disqualify all numbers above your threshold, that start with the same number as your threshold. For this, you recurse (removing the first number of your threshold, and decreasing the number of required "1" in your representation by 1 if your threshold first digit was "1".
Thanks a lot
The initial approach to the question revolves around thinking that the maximum number of ones that can come in the binary representation of a number n<2^1000 will be 1000. Thus, just in one step, from a large number, you will have reduced second level number less than or equal to 1000. Also, now you will be left with k-1 operations as you used one before. You can precompute the number of steps required for all i from 1 to 1000 to be reduced to 1 in an array, say arr[]. For all i's, if arr[i]==k-1, that means you have to place i number of 1's in a string of size l(size of given number's string in binary representation) such that the number formed doesn't exceed the given number n. This can easily be done by one simple "for" loop. You permute these using nCr function which one must mind to precompute for 1<=n<=1000 and 1<=r<=1000, otherwise will give TLE. Also mind special cases like n=1 and k=1.
In the function cntperm , why are you doing temp--?? I am not able to understand this part!
In the function cntperm(), temps hold the number of 1's that I have to place after index i. So, say for string 10011001, if temp=2, the first iteration(i=0) calculates the number of ways that exist which have a '0' at index i=0 and two 1's after i=0. The answer will be 7C2. By placing 0 at index i=0 and 2 1's only after that ensures that all the permutations produced are less than the given number. Now, I place '1' at i=0 and move forward in the next iteration i.e i=1. So the remaining number of 1's that I will be working with will be 1 less than the previous count that is temp-1. That's why I am doing temp--. Also, if I have used all the ones (when temp becomes 0), I am left with no more permutations except that I fill all the remaining places after that by only zeros. So, I increase the count by one for one final time and exit the loop.
Great explanation. Thanks for taking time and explaining!
Solution to D is wrong.
Consider Following test case.
4
4 4 7 4
1
1 1 4 2
The problem statement states that He considers the guess to be almost correct if he can change at most one element in the segment such that the gcd of the segment is x after making the change
The answer should be NO, because if we change 7, gcd of segment become 4, else gcd of segment is 1. In no case we can make gcd of range 2. I didn't even implement, because of this.
Shouldnt the problem state that gcd of segment shall be divisible by x for your solution to be correct???
EDIT: got my mistake... Sorry
I think you could change the third element in the array to be 2, and the gcd will become 2, so it don't need to state that gcd of segment shall be divisible by x.
I already got my mistake (even edited my comment above).
Thanks for reply.
Can someone tell me why this solution34419524 got accepted for problem A(Perfect Squares) since sqrt of negative numbers gives 'nan'.
Because any operation with NaN gives a NaN and NaN is unequal to itself.
floor(NaN)is NaN,ceil(NaN)is NaN,NaN != NaN, and hencefloor(NaN) != ceil(NaN), so the program thinks “this (negative) number is not a square”, which is correct.Can someone please elaborate the solution of problem E ? It's almost impossible to understand it from the given editorial ?
First root the given tree on its centroid. Now for each node u, masku has at jth bit in binary representation of masku, considering count of characters from root to u. We can say that a path from u to v is palindromic if
at jth bit in binary representation of masku, considering count of characters from root to u. We can say that a path from u to v is palindromic if 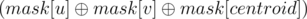 has at most 1 set bit.
has at most 1 set bit.
Now let partv be defined as subtree of vertex v such that v is children of the centroid. Now we consider all paths that include centroid. For each node u, valid paths are the paths ending in part other than partu, and starting from any node in subtree of u including itself and satisfying the above property.
Valid masks for a node u are: mask[u] and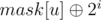 . Let otheru be the sum of all valid masks from other parts for u. So for u, otheru will be
. Let otheru be the sum of all valid masks from other parts for u. So for u, otheru will be 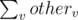 such that v lies in its subtree (including itself) . Hence add it to the answer. For root (centroid), answer will be summation of cnt1[mask[u]]·cnt2[maskx] for all u, such that cnt1 is count of masks in part of u, and cnt2 is count of masks in other parts and maskx are valid masks of u.
such that v lies in its subtree (including itself) . Hence add it to the answer. For root (centroid), answer will be summation of cnt1[mask[u]]·cnt2[maskx] for all u, such that cnt1 is count of masks in part of u, and cnt2 is count of masks in other parts and maskx are valid masks of u.
Now solve recursively for each of the parts.
Can you please explain the role of dfs1() & dfs2() function?
dfs1() calculates the mask for each vertex. dfs2() calculates the answer for each vertex. dp[u] is the the number of paths starting from subtree of u and ending in any other part.
cnt[0] and cnt[1<<i](for i=1:20) are added to dp[r] only once. where are these added twice? As we are making ans[r]=dp[r]/2, shouldn't those cnts be added twice?? Can you please describe the second position?
Paths which go from one part to another are counted twice. And we add paths from u to root once when we solve for each vertex u. To make their count twice, we add paths from root to u again. Now we add dp[r]/2 to the ans.
Can you please elaborate how we get the paths from nodes that we've already removed as centroids? I read the explanation twice but couldn't understand how that's resolved. Thanks
EDIT: nvm, it is very simple, just add the aggregated values to the nodes when you dfs.
EDIT 2: oops still 6 hours of queue that I forgot about
Problem E editorial is not clear. Please, somebody explain it better.
This might be helpful.
Can somebody please explain me the computations being done in the ncr matrix? I understand what is being done there but not how. Thanks!
You can compute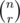 using the identity
using the identity 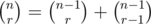 .
.
why ans need to substract 1 for k==1?
I am not able to understand what this code segment of the 3rd question doing.Can anyone help me?
As the solution says, we can bruteforce all the possible prefixes. So I refers to which bit we are up to, since the first difference should be x[i]=1,y[i]=0 (otherwise it clashes with the constraint)
Say we have used “nones” 1s, we are going to pick the left 1s we can pick to insert into the suffix. The number of such thing can be calculated by binomial coefficients.
Would anyone like to explain the solution to F which is created Syloviaely? appreciate it :)
I am gonna give it a try.
Notice that in bitset x[i] the positions on the original string that have character 'a'+i are set to 1. For example if the original string is "hahati" we will have 2nd and 4th bit of x[0] set and X[7] will have 1st and 3rd bit set to 1 and so on. I think you can easily figure out how the update operation was done.
Now for query, at the beginning all bits of ans are set. Now let's see what happens at the very first iteration in the for loop of 1 to len. An AND operation was done with the bitset of corresponding character with 1 right shift. What will it do? It will kepp the 0th bit of ans set and all other bits with same relative distance as in the characters bitset. For example if our query string is "ha", our first character is 'h' so an AND operation with X[7]<<1 will keep 0th and 2nd bit of ans set to 1 and all other reset to 0. Second character is 'a', a right shift with 2 for X[0] will keep 0th and 2nd bit set and after AND with ans 0th and 2nd bit of ans is set. We do this for all characters in the string and if even a single character doesn't match along the way corresponding bit will be reset to 0. For example if we had "hat" as our query on the third iteration for character 't' 0th bit will be reset to 0 but the 2nd one won't.
This way ans will store all the positions where a query string starts as substring in the original string. But we don't need all the positions, only the positions between l to r-len+1. That's what was done in the last line.
Here is the solution in question if someone was wondering.
get it, ty :)
can you please explain the query part with an example. I never used bitset so, having difficulty in understanding this. Thanks!
can anyone please help me with my code for F : solution It is giving MLE. I used suffix tree and it requires O(n) space and so my complexity will be around O(n*28). I am unable to figure out the reason please help me.
Please someone explain the editorial of Problem E
This might be helpful.
In solution of problem H para.7: "where tree[i][any] is the number of trees of i vertices with any root degree from 1 to d. " Maybe I think there's a mistake: not d but d-1 ?
And could someone explain how to calculate the denominator of value c in module p which is not guaranteed a prime ? Thanks a lot.
Yes, you're right. It should be d - 1. The editorial has been updated. Thanks!
As for your second query, observe that
and
so
Got it. Thank you very much.
Need help Problem D: Keep getting TLE, can't understand why, should be pretty fast. http://codeforces.com/contest/914/submission/34645114
In the editorial for problem C,
For each x (x < 1000) such that x has order k - 1, we need to compute the number of numbers less than or equal to n that have k set bits.
Don't you mean,
For each x (x < 1000) such that x has order k - 1, we need to compute the number of numbers less than or equal to n that have x set bits.
Yes, you are right. Since we are using 1 step to go from n to x and now x must have order of k — 1.
In the author's solution to C, what does the following piece of code do
Yes, can someone please explain this, it is not quite clear whether the following case "10000..00" (zeroes = length(n) — 1) is being excluded (but why?) or something else is taken care by this statement?
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int tests=1; //freopen("input.txt", "r", stdin); // freopen("output.txt", "w", stdout); //cin>>tests; {
string s; cin>>s; int k; cin>>k; int c1 = 0,c0=0; for(int i = 0;i<s.size();i++) { if(s[i]=='1') c1++; else c0++; } k--; int dp[c1+1]; dp[0]=0; memset(dp,0,sizeof(dp)); for(int i = 1;i<=c1;i++) { int x = i,c=0; while(x!=1) { if(dp[x]!=0) { dp[i] = c+dp[x]; break; } c++; int y = x,j=0; while(y!=0) { if(y%2!=0) j++; y=y/2; } x = j; } if(dp[i]==0) dp[i] = c; } // rep(i,0,c1+1) // cout<<dp[i]<<" ";
ll ans = 0; for(int i = 1;i<=c1;i++) { if(dp[i] == k) { ans = (ans%hell + nCrModp(s.size(),i,hell)%hell)%hell; } } cout<<ans; }}
this is the code for C can someone help me that where i M wrong.
Help For C
int main() {
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); int tests=1; //freopen("input.txt", "r", stdin); // freopen("output.txt", "w", stdout); //cin>>tests; {
string s; cin>>s; int k; cin>>k; int c1 = 0,c0=0; for(int i = 0;i<s.size();i++) { if(s[i]=='1') c1++; else c0++; } k--; int dp[c1+1]; dp[0]=0; memset(dp,0,sizeof(dp)); for(int i = 1;i<=c1;i++) { int x = i,c=0; while(x!=1) { if(dp[x]!=0) { dp[i] = c+dp[x]; break; } c++; int y = x,j=0; while(y!=0) { if(y%2!=0) j++; y=y/2; } x = j; } if(dp[i]==0) dp[i] = c; } rep(i,0,c1+1) cout<<dp[i]<<" ";
ll ans = 0; for(int i = 1;i<=c1;i++) { if(dp[i] == k) { ans = (ans%hell + nCrModp(s.size(),i,hell)%hell)%hell; } } cout<<ans; }}
in div2 c..whenever k==1 then an extra count will appear for value ==1...becoz 1 has count of ones ==1 ans dp[cnt]=dp[1]=0(k-1).. if(i == 0 && k == 1) { ans = (ans+MOD-1)%MOD; } this code is only to avoid this condition..:)
For 914C — Travelling Salesman and Special Numbers, one can simply use
__builtin_popcount()to replace theones()function in the editorial.Bye.
I've been struggling with D for several hours now. Here is my submission: https://codeforces.com/contest/914/submission/91172586.
I'm using the efficient segment tree from https://codeforces.com/blog/entry/18051 blog. The cnt function counts how many bad gcds there are, and should be O(log(n)) as you go down at most one branch of the binary tree. Cnt is called at most once every query, so the total complexity of each query should be log(n). However, I am getting TLE on test #8 and I have no idea why.
Any help would be greatly appreciated. I have just learned segment trees and this is part of my practice for segment trees, so I may just be using it incorrectly. The code passes the first 7 test cases though, so I'm at a loss.
Sorry for bumping this, but isn't the time complexity for D O(q*n*log(n))?
I got this complexity from the factor of q from the number of queries, the log n from decomposing the original range, and a factor of n to check if a node works if it is not a multiple of n.
If this is true, won't the program TLE? Or is my complexity wrong?
In problem D, The size of the arrays in the solution code are much smaller than the task's requirement. When node is 5e5, will arrays' index overflow occur?
can E be done without using centroid decomposition.
Problem D: For those who are getting TLE using segment tree and binary search. When printing yes or no, Using endl instead of "\n" and defining int as long long(I know its silly, but i do it not to get overflow somewhere in my code) gave me TLE.Here's my codes.
TLE: https://codeforces.com/contest/914/submission/248670501
AC: https://codeforces.com/contest/914/submission/248670606