Hi, I’d like to introduce a simple trick about segment tree in this blog as I promised in this comment. Sorry for the long delay, as a sophomore in Peking University, I've just finished a tired semester and a painful final exam. And now I finally have enough time to do a simple introduction to this interesting algorithm.
It may be a huge project for me since my English is not good. I think I will finish this blog in several steps and I will try to finish it as soon as possible :)
In China, all of the 15 candidates for the Chinese National Team are asked to write a simple research report about algorithms in informatics Olympiad, and the score will be counted in the final selection. There are many interesting ideas and algorithms in these reports. And I find that some of them are quite new for competitors in CF although they are well known in China from the final standings of some recent contests. For example, In the last contest CF Round #458, the problem G can be easily solved using "power series beats" (Thanks for matthew99 to give this name :)) in O(2nn2) which was imported in China by vfleaking in 2015.
This blog is about my report which is written about two years ago. I am satisfied with this work although there is a flaw about time complexity. xyz111 gave me a lot of inspiration, and the name “Segment tree beats” is given by C_SUNSHINE which is from a famous Japanese anime “Angel Beats”.
Here is the link about the Chinese version of this report.
Part1. What it can do.
This work has two parts:
- Transform interval max/min (for
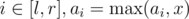 ) operations into interval add/subtract operations in O(1) or
) operations into interval add/subtract operations in O(1) or 
- Transform history max/min/sum queries into interval max/min operations in O(1).
Here are some sample problems I used in my report. At first you have a array A of length n and two auxiliary arrays B, C. Initially, B is equal to A and C is all zero.
Task 1. There are two kinds of operations:
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - Query for the sum of Ai in [l, r]
It can be solved in 
Task 2. We can add more operations to Task 1:
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - For all
 , change Ai to min(Ai, x)
, change Ai to min(Ai, x) - For all
 , change Ai to Ai + x, x can be a negative number
, change Ai to Ai + x, x can be a negative number - Query for the sum of Ai in [l, r]
It can be solved in  and I could not proved the exact time complexity yet, maybe It is still
and I could not proved the exact time complexity yet, maybe It is still  ;)
;)
Task 3. And we can query for some other things:
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - For all
 , change Ai to min(Ai, x)
, change Ai to min(Ai, x) - For all
 , change Ai to Ai + x, x can be a negative number
, change Ai to Ai + x, x can be a negative number - Query for the sum of Bi in [l, r]
After each operation, for each i, if Ai changed in this operation, add 1 to Bi.
It’s time complexity is the same as Task 2.
Task 4. We can also deal with several arrays synchronously. Assume there are two arrays A1 and A2 of length n.
- For all
 , change Aa, i to min(Aa, i, x)
, change Aa, i to min(Aa, i, x) - For all
 , change Aa, i to Aa, i + x, x can be a negative number
, change Aa, i to Aa, i + x, x can be a negative number - Query for the max A1, i + A2, i in [l, r]
It can be solved in  and if there are k arrays, the time complexity will be raised to
and if there are k arrays, the time complexity will be raised to 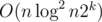 .
.
Task 5. And there are some tasks about historic information.
- For all
 , change Ai to Ai + x, x can be a negative number.
, change Ai to Ai + x, x can be a negative number. - Query for the sum of Bi in [l, r].
- Query for the sum of Ci in [l, r]
After each operation, for each i, change Bi to max(Bi, Ai) and add Ai to Ci.
The query for Bi can be solved in  and the query for Ci can be solved in
and the query for Ci can be solved in  .
.
Task 6. We can even merged the two parts together.
- For all
 , change Ai to max(Ai, x)
, change Ai to max(Ai, x) - For all
 , change Ai to Ai + x, x can be a negative number.
, change Ai to Ai + x, x can be a negative number. - Query for the sum of Bi in [l, r].
After each operation, for each i, change Bi to min(Bi, Ai).
It can be solved in 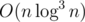 .
.
There are 11 sample tasks in my report and here are 6 of them. All of them are interesting and are hard to solve using the traditional techniques such as lazy tags.
Part2. The main idea
Interval min/max operations
To make the description clearer, I think it’s better to introduce an extended segment tree template.
I think most of the competitors’ templates of the lazy tag is like this ([l, r] is the node's interval and [ll, rr] is the operation's interval):
void modify(int node, int l, int r, int ll, int rr) {
if (l > rr || r < ll) return;
if (l >= ll && r <= rr) {
puttag(node); return;
}
pushdown(node);
int mid = (l + r) >> 1;
modify(node * 2, l, mid, ll, rr);
modify(node * 2 + 1, mid + 1, r, ll ,rr);
update();
}
The main idea is return whenever we can, put the tag whenever we can:
- When the operation's interval and the node's interval are no longer intersected, the information inside this subtree must not be affected. So we can return immediately.
- When the node's interval is contained by the operation's interval, all the information inside the subtree will be changed together. So we can put the tag on it and return.
In other words, we can replace the two conditions arbitrarily, i.e., we can extend the template like this:
void modify(int node, int l, int r, int ll, int rr) {
if (break_condition()) return;
if (tag_condition()) {
puttag(node); return;
}
pushdown(node);
int mid = (l + r) >> 1;
modify(node * 2, l, mid, ll, rr);
modify(node * 2 + 1, mid + 1, r, ll ,rr);
update();
}
What's the use of such a modification? In some advanced data structure tasks, it's impossible for us to put tags in such a weak condition l >= ll && r <= rr. But we can put it when the condition is stronger. We can use this template to deal with this kind of tasks but we need to analyze the time complexity carefully.
Simple task: There are three kinds of operations:
- For all
 , change Ai to
, change Ai to 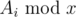
- For all
 , change Ai to x
, change Ai to x - Query for the sum of Ai in [l, r]
It's a classic problem (it's the simple extension of 438D - The Child and Sequence) and the traditional solution is to use balanced tree such as splay/treap to maintain the continuous segments with the same Ai and for operation 2, we find out all the segments with Ai ≥ x and change the value of each one.
But if we use segment tree, we can get a much simpler solution: let break_condition be l > rr || r < ll || max_value[node] < x and let tag_condition be l >= ll && r <= rr && max_value[node] == min_value[node]. And we can find that the time complexity of this segment tree is also  .
.
And now, we can easily describe the main idea of "segment tree beats". For each node, we maintain the maximum value max_value[node] and the strict second maximum value second_value[node].
When we are doing the interval min operation for number x. let break_condition be l > rr || r < ll || max_value[node] <= x and let tag_condition be l >= ll && r <= rr && second_value[node] < x. Under such an condition, after put this tag, all of the maximum values inside this subtree will be changed to x and they are still the maximum values of this subtree.
To make it easier to merge with other operations, we can maintain the values in this way: For each node, we maintain the maximum value inside this subtree and other values separately (the maximum values are the first kind and others are the second). Then, interval max operation will be changed to "add a number to the first kind values in some intervals". Keep the meanings of each kinds of values and the tags, you will find that the processes of pushdown and update will be much clearer.
That's the main idea of the first part of "segment tree beats". It is very simple, right? And it also has a very nice time complexity. (I will give out the proof of the time complexity in the third part of this article).
And let's see the first two sample tasks in part 1.
Task 1. In this task, we can maintain the number of the first kind of values inside each node t[node], and when we put tag "add x to the first kind values in this subtree", the sum will be added by t[node] * x. Then we can easily maintain the information we need.
Task 2. In this task, we can maintain the maximum values/ minimum values and others separately, i.e., there are three kinds of numbers now, and we will use three sets of tags for each kind of values. Also, to deal with the queries of the interval's sum, we need to maintain the numbers of the first kind and the second kind of values. Pay attention to some boundary conditions, if there are just two different values in this subtree, there will be no third kind of values and if all the values are the same, the set of the first kind and the second kind will be the same
Historic information
In this part, we will focus on three special values which I named "historic information":
- historic maximal value: after each operation, change Bi to max(Bi, Ai)
- historic minimal value: after each operation, change Bi to min(Bi, Ai)
- historic sum: after each operation, add Ci by Ai.
You may wonder why we need to consider these values. But in China, there had been several problems about these values before I wrote this report. And maintaining these values is a much harder task than it looks like. Here is a data structure task in Tsinghua University Training 2015:
Sample Task: Here is the link of this problem. There are five kinds of operations (x is a positive integer.):
- For all
 , change Ai to Ai + x.
, change Ai to Ai + x. - For all
 , change Ai to max(Ai - x, 0).
, change Ai to max(Ai - x, 0). - For all
 , change Ai to x.
, change Ai to x. - Query for Ai.
- Query for Bi.
After each operation, change Bi to max(Bi, Ai).
To solve this task, ordinary segment tree is enough. But It's not easy to deal with the relationship between the lazy tags and the historic information. I think it's a good sample problem to show the features of historic information.
We have already gotten the way to deal with the interval min/max operations. And they are good tools to maintain historic information.
Now, let use consider such a kind of problems (Part1. Task 5): interval add/subtract, query for the interval sum of historic information. It's quite hard since we can't just use the traditional lazy tag technique to solve it. But we can use an auxiliary array Di with the initial value of all zero to do some transformation:
- Historic maximal value: let Di = Bi - Ai. Then if we change Ai to Ai + x, Di will be changed to max(Di - x, 0).
- Historic minimal value: let Di = Bi - Ai. Then if we change Ai to Ai + x, Di will be changed to min(Di - x, 0).
- Historic sum: let Di = Ci - tAi while t is the current operation id. Then if we change Ai to Ai + x, Di will be changed to Di - (t - 1)x.
We can use the technique introduced in the previous part about interval min/max operations to maintain the sum of Di. And then we could get the sum of Bi or Ci.
What's more, since we have already transformed interval min/max operations to interval add/subtract operations, we can also maintain the interval sum of historic information under interval min/max operations (Part1. Task 6). This is a simple expansion and I think it's better to leave it as an exercise.
Part 3. The time complexity
In this part, I will give the proofs of the time complexity of Part 1 Task 1 and Part 1 Task 2. You can find that the proof of Task 2 is universal: it is equally applicable to Task 3 to Task 5. And Task 6 can be regarded as two layer nested “segment tree beats”. It's time complexity can be proved using the same way as Task 2.
Task 1
In this part, we will proof the algorithm showed in Part 2 of this problem is  : interval min operation, query for the interval sum.
: interval min operation, query for the interval sum.
gepardo has given a clear proof to show the time complexity of this problem is  in this comment. Here, I'd like to show another proof which is much more complex. But I think it is my closest attempt to proof Task 2 is
in this comment. Here, I'd like to show another proof which is much more complex. But I think it is my closest attempt to proof Task 2 is  . And this proof will show the relationship between "segment tree beats" and the solution of this problem given by xyz111 (you can find this solution in this website. The name of this problem is "Gorgeous Sequence" and the solution is written in English).
. And this proof will show the relationship between "segment tree beats" and the solution of this problem given by xyz111 (you can find this solution in this website. The name of this problem is "Gorgeous Sequence" and the solution is written in English).
The main idea is to transform max value into tags. Let the tag of each node in segment tree be the maximum value inside its interval. And if a node has the same tag as its father, we will remove the tag on it. Here is an simple example:
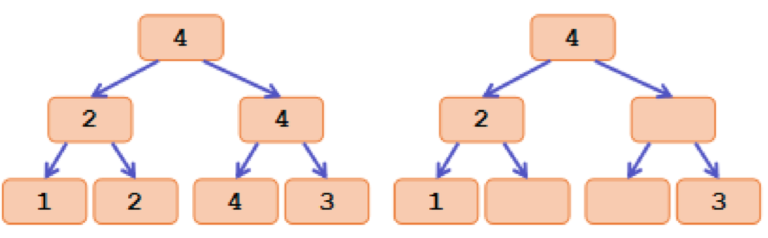
The left picture shows the maximum value of each node in a segment tree of array [1, 2, 4, 3]. And the left picture is the tags.
After the transformation, we can find that the strict second maximum value we maintained is just the maximum tag inside each subtree.
One important property of these tags is each tag is strictly greater than the tags inside its subtree. But why this property still holds after interval min operations? Consider the difference between this algorithm with the original segment tree: We will visit more nodes when second_value[node] >= x. This process ensure that we will put a tag only if all the tags inside this subtree is smaller than the new tag, i.e., we visit these large tags and delete them.
When do the tags change? One possibility is after an interval min operation, we will delete some tags and add some new tags. And another possibility is that if we just change some of the values inside the node, the previous tag may be pushed down after pushdown() (The maximum value of this subtree may be changed.)
For the convenience of description, let us define tag classes:
- All the tags added in the same interval min operation belong to the same tag class.
- After a pushdown, the new tag belongs to the same tag class as the old tag.
- Any two tags which do not satisfy above two conditions belong to different tag classes.
And we can divide the nodes we visit in a single interval min operation into two sets: ordinary nodes and extra nodes. Ordinary nodes are those nodes which an ordinary segment tree also visit in an operation of [l, r], and extra nodes are those nodes which we visit because the stronger break_condition.
Then, let w(T) (T is a tag class) be the number of nodes which has at least one tag in T inside its subtree, and let the potential function Φ(x) be the sum of w(T) for all existing T.
Since there are at most n tags in the segment tree, so the initial value of Φ(x) is  . Consider the influences to Φ(x):
. Consider the influences to Φ(x):
- After a
pushdown(), the old tag will be pushed down to two children ofnode, so Φ(x) will be increased by 2. - The new tag will occur on only ordinary nodes. So for the new tag class T, w(T) is
 . Since the number of ordinary nodes is
. Since the number of ordinary nodes is  .
. - The reason we visit an extra node is that we need to delete some tags inside its subtree. And a clear fact is that if we delete a tag in tag set T inside a subtree, all the tags in T inside this subtree will be also deleted. So, after visiting each extra node, Φ(x) will be subtract by at least 1.
Since the total increase of Φ(x) is  and each extra node will subtract 1 from Φ(x), we know that the time complexity is
and each extra node will subtract 1 from Φ(x), we know that the time complexity is  .
.
You may find that this potential function is just the same as the proof given by [usr:gepardo]. But using tags can bring us much more useful properties, and we can come up with some useful potential functions from the tags of which the definitions can be very strange if we want to define them just from the values. You may see it from the proof of the task 2.
Task 2
In this task, we will still use the tags defined in previous proof, and the potential function we choose is a little strange: let d(t) ( t is a tag ) be the depth of t in the segment tree and Φ(x) be the sum of d(t) for all existing tags. And since d(t) is  and the number of the tags is no more than n. So the initial value of Φ(x) is
and the number of the tags is no more than n. So the initial value of Φ(x) is  .
.
Then, let's consider the influences to Φ(x):
- After an interval min operation, there will be no tags on the extra nodes. So we can just consider
pushdownon ordinary nodes (For the interval add/subtract operations, we visit only ordinary nodes, so the following discussion is still correct) . And after apushdown, the old tag will be pushed down to the two children ofnode, and Φ(x) will be added by . Since there are
. Since there are  ordinary nodes,
ordinary nodes, pushdownwill make Φ(x) increased by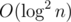 each interval min operation.
each interval min operation. - The new tag will occur on only ordinary nodes, so it will also make Φ(x) increased by
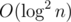 .
. - Each extra node will make Φ(x) decreased by 1 because there must be a tag deeper than this node which is deleted after this operation.
Since the total increase of Φ(x) is  and each extra node will subtract 1 from Φ(x), we prove that the time complexity is
and each extra node will subtract 1 from Φ(x), we prove that the time complexity is  .
.
What's more, in this proof, we do not use any special properties of interval add/subtract operation. So the proof is still hold for other operations. That's why I call this proof universal.
So far, this article is finished. I've never thought that it will be so popular. Thanks a lot for the encouragement and the support. I hope this article can help :)












The research reports from candidates for the Chinese National Team are publicly available?
Sure, but we have only Chinese version qwq
Can you provide a link of all those reports of the lasts years??
You could find them with 國家集訓隊XXXX論文集(where XXXX is the year)
Also I've found some of them from Voleking 's github
Thank you very much!!!
Thanks for jiry_2 and other Chinese guy for those amazing thoughts, lol
I said why I got so many stars recently_(:з」∠)_
Please, post them :D
The research component of the Chinese OI camp sounds amazing. It would be really good if the reports could be shared/translated for the rest of the world as well.
Definitely agree! I'm so sad Chinese is so hard to translate. Maybe some Chinese volunteers would try to translate them. I'd pay for that... Right now I'm more interested in what are the most useful pieces of work of this kind? If this is just one of them, I can't imagine how much these tricks achieve
Btw if someone agrees to translate them, I'm also willing to pay, as judging by the already translated Chinese "tricks" and data structures these should also be nice and useful.
By the way, if you want to publish it on e-maxx-eng too, it should be easy enough as both blogs at CF and e-maxx-eng use MarkDown and TeX. And I'm ready to help if needed. :)
Set power series (I don’t know how to describe it in English so I just use the phrase given by Baidu translate)
Hmmm...I don't know the official name for this term either. What about "power series beats". It just sounds as sassy as "segment tree beats".
Finally ! I've been waiting for this post for such a long time. I used to translate the Chinese version by Google Translate and it was really hard to understand lol.
Btw, here are some problems which (i think) can be applied Segment Tree Beats to:
HDU Gorgeous Sequence (this is pure, basic STB)
Bear and Bad Powers of 42
Nagini
Little Pony and Lord Tirek
Julia the snail
Thanks for great post ! Looking forward to seeing your next post about Complexity.
Actually... 453E - Little Pony and Lord Tirek An ordinary segment tree is enough.
Thanks a lot. I know the first two problems can be solved this way and I will check the remaining three problems once I have chance to use computer.
BTW, I've published some exercises about it on some Oline Judges in China. I'll give out the links later, too.
Here are the links of some exercises:
Well, I think I made some mistakes yesterday. Maybe "segment tree beats" can not help with solving the second task?
And I think the task 1,3,4 are good exercises of this article. Thanks a lot!
I am unable to come up with a solution using Segment Tree Beats for the mentioned Task 3 — 453E — Little Pony and Lord Tirek. Here is what I tried:
->
x=[Tj - T(j-1)]->
S[i] for i in [1, N] = min(S[i]+x*R[i], M[i])-> Break into 2 parts, First update tag condition:min_Mi-Si/Ri<x, 2ndmin_Mi-Si/Ri>x. Update isadd cnt*(min_Mi-Si/Ri - x)where cnt is the number of nodes having the given min value in the range. (Upd1)-> Then
add x to S[i] for i in [1, N]. (Upd2)->
ans+=sum of S[i] of (Lj to Rj)Query->
S[i] of (Lj, Rj) = 0(Upd3)The values are defined as in the problem statement, but S[i] is now the current mana of a pony.
Issue: When I perform the add x update, I lose control over the Min tags because on subtracting/adding a constant to the numerator of a fraction it is not necessary that these fractions remain in order(S[i] is getting added by x, hence numerator is subtracted by x). This whole thing depends on Ri and I could now have an arbitary min tag for this node's range. This is thus unlike the normal add x queries where there was no multiplication/division factor on the values involved.
It would be of great help if someone could either help me redefine my approach or tell me if this problem really isn't an application of Segment Tree Beats.
Just btw, thanks jiry_2. This article had me engrossed for days and the fact that a lot has been left to the imagination and thinking of the reader. Even tough to understand english does help in places as it forced me to discuss and think. It wouldn't have been fun had every reasoning been given.
How problem G (CF round 458) can be solved in O(2n * n2), if n = 1000000?
I think he meant n = 17 for that problem
What means "history informations" in task 5?
Could be going about pertistency.
I don't think so. Because persistency for this segment tree is the same as for standard segment tree.
Sorry for the confusing description. "history information" means the value inside array B and C since Bi is the minimum value and Ci is the sum of the values on this position among all previous versions.
I'm so sorry for the stupid spelling mistakes in this blog such as "informations". I will try to fix them tonight qwq.
But I don't understand how can we use B and C. Or they'll help in some tasks?
Well, I put this inside my report because there are some data structure tasks about historic information in China, and I find that this kind of tasks can be easily solved in this way.
I have not thought about the applications of these values qwq.
Array B and C contains the historical information,which array B means the historical maximum value and array C means the sum of all the versions
What about code?
I think it'll be a good idea to require all the reports written in English from now on,since i'll never have a chance of writing one.>_<
Auto comment: topic has been updated by jiry_2 (previous revision, new revision, compare).
Another tutorial post on the same topic (In Chinese): http://www.shuizilong.com/house/archives/hdu-5306-gorgeous-sequence/
Great article! I didn't manage to solve even task 1.
I felt that this technique is somewhat similar to the solution of 453E - Little Pony and Lord Tirek, but segment tree beats seem more advanced and general.
Can you please upload these task series in some online judge like SPOJ? It will be really helpful.
This is not a bad idea tbh, why so many downvotes? It could be like the next STB1, STB2, STB3, ..., like QTREE and COT etc.
It seems that task 2 is still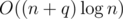 . I have a proof for it.
. I have a proof for it.
Let's denote the value C. C is a sum for all the D[l... r] where [l... r] is a segment in the segment tree. D[l... r] is a number of distinct numbers on a segment [l... r]. It's not hard to see that initially C doesn't exceed . Also, C will increase on at most
. Also, C will increase on at most  each update query.
each update query.
It's obvious that for each query we can go to more than into segments. Some segments we visit I will call extra. An extra segment is a segment for which l ≥ ll && r ≤ rr && second_valuenode ≥ x && max_valuenode ≥ x, i. e. the segment coincides with our query and we are not returning due to break condition or tag condition. Each extra segment processing takes O(1) (maybe from this extra segment we will go to some other extra segments, but we'll consider each extra segment separately, without its children, in this proof). How C changes if we process an extra segment? All the values equal to second_value and max_value inside this segment will be replaced with the query parameter, so the number of distinct numbers is decreased by at least one, i. e. C will be decreased by at least one for each extra query. The same is held both for minimum or maximum updates.
segments. Some segments we visit I will call extra. An extra segment is a segment for which l ≥ ll && r ≤ rr && second_valuenode ≥ x && max_valuenode ≥ x, i. e. the segment coincides with our query and we are not returning due to break condition or tag condition. Each extra segment processing takes O(1) (maybe from this extra segment we will go to some other extra segments, but we'll consider each extra segment separately, without its children, in this proof). How C changes if we process an extra segment? All the values equal to second_value and max_value inside this segment will be replaced with the query parameter, so the number of distinct numbers is decreased by at least one, i. e. C will be decreased by at least one for each extra query. The same is held both for minimum or maximum updates.
But, as we know, C can be increased at most by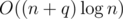 , so we will visit no more than
, so we will visit no more than 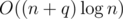 extra vertices. So, we proved the time complexity.
extra vertices. So, we proved the time complexity.
Correct me if I am wrong.
I've considered this potential function before. But the main problem is that the potential function will be changed a lot after an interval operation. Here is an example: A is an array of length 2n and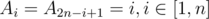 . Then if I add n to all Ai in [1, n]. C will be increased by O(n).
. Then if I add n to all Ai in [1, n]. C will be increased by O(n).
BTW, you have already gotten the way to prove the time complexity of task 1. It's a very clear proof and I even want to just copy your comment in my next update :)
Thanks a lot!
You are welcome :)
By the way, I noticed that I misread the task 2. I didn't notice the adding to a segment. If we have no
A[i] += xoperation, justA[i] min= xandA[i] max= x, the proof works.Auto comment: topic has been updated by jiry_2 (previous revision, new revision, compare).
I have read the Chinese version before, but I can't truly understand it until I read this post with those codes, thanks a lot.
You're welcome :)
I try another way to write this article. I believe it's much clearer than the word description in the Chinese version.
In the end of the article there are 3 paragraphs, I think that in the second one it must be written "Historic minimal value", not maximal. Aren't I right?
Oh, I forgot to change it after copying from the first line. I've fixed it, thanks a lot.
Auto comment: topic has been updated by jiry_2 (previous revision, new revision, compare).
You've failed a little bit again) Part 3, Task 1, end of the second paragraph. I think that [usr:xyz111] isn't exactly what you wanted to write) (Sorry for my remarks)
In part 3, it seems that the proof of task 2 doesn't make use of the property of "depth" and only counts the number of tags. I think we can achieve a better bound if we slightly change the potential function.
Let's define the potential as the number of tags in the segment tree, i.e. set d(t) to a constant function 1. Then the increases in the potential caused by interval min operation and new tags become instead of
instead of 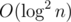 (because we don't sum the depth but simply count the occurrence) and the visit of each extra node still decreases the potential by 1 (removal of a tag). As a result, the total increase in the potential is
(because we don't sum the depth but simply count the occurrence) and the visit of each extra node still decreases the potential by 1 (removal of a tag). As a result, the total increase in the potential is 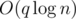 , and the overall time complexity is bounded by
, and the overall time complexity is bounded by 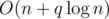 (the initial value of the potential is at most n).
(the initial value of the potential is at most n).
Please correct me if I am wrong.
Well, to remove a tag, you may visit at most extra points. That's why I use the depth: each visit will absolutely make Φ(x) decrease by 1 :)
extra points. That's why I use the depth: each visit will absolutely make Φ(x) decrease by 1 :)
So please say if this is correct.
If we consider your potential function, can we use it to also prove the complexity of task 1. It seems to me that you are just counting the number of tags basically. So, in the first task, we add only 1 or 2 new tags in the worst case during a update because new tags will only be added on the extremal terminal nodes.. ie.. on the terminal nodes that are to the extreme left and right. And we use atmost logn operations to delete a tag. Since there can be total o(n) tags we take nlogn time to delete and so total complexity is nlogn.
However, is my observation correct that in the first task, where there are no increase operations for the values through range increment, using ur potential function we get only o(1) additions.
(I am trying to explain both the tasks using the same potential function.. hence this attempt)
I tried to code this tree for Gorgeous Sequence based on your description and got AC within 22XX ms
I stored in each node the 1st & 2nd maximums, sum and count of numbers = 1st maximum and when 1st maximum of a child is bigger than the parent's I do lazy propagation
My code if anyone is interested: Github
What s the meaning of "tags"? I thpught they were conditions where we dont transverse down the tree anymore. But as i read on i started to to get confused :/.
Can someone please provide neat code for task 2? I have a lot of problems with implementation when there are minimum, maximum and addition.
Ok, I don't understand even the first simple task. Even the break condition: max_value[node] < x. For second operation you also have to change smaller values than x, it's just an assignment. Why shouldn't we bother with A[i] < x?
Besides there are 2 types of update operation but there is only one type of break condition and tag condition described. Also the explanation of the traditional solution is not understandable, because of the same reason I wrote above: "and for operation 2, we find out all the segments with Ai ≥ x and change the value of each one." — this is just an assignment, so why can we omit smaller values...?
Can you or somebody provide code with comments for some tasks brought up in part one please, for clarity. I have read the article, but maybe in this case, some pieces of code would make it clearer.
Links to some complicated problems that uses that ideas??????
similar to task 1:
https://www.hackerrank.com/challenges/box-operations/problem https://csacademy.com/contest/round-70/task/and-or-max
similar to task 5:
https://codeforces.com/contest/997/problem/E
Thanks a lot, I already got stuck in csacademy's and-or-max problem at the contest. I'll try to solve it using this aproach.
Could someone explain how task 4 should be implemented? I don't really know how to deal with minimizing the sum of the two different arrays.
Can someone say if the definition of tags change from part 1 of the blog to part 3 task 1 of the blog? If yes, then please briefly describe the new definition in part 3 task 1. If no, then how does transformation of max values to tags work. Also, why does new tag only occur in only old nodes(Task 3 part 1)?
Thank you in advance to whoever helps me out.
Can someone explain how the time complexity is still O(N*log2(N)) for this http://codeforces.com/contest/438/problem/D problem (with the range modulo updates)? From what I can see, the tag condition is even more strict than Task 2, and I can't intuitively see how it still has the same complexity.
Sure, first let's make the break condition be x > max in range (l,r) , since if this condition is fullyfied we cannot change anyone in [L,R] , let's try to found a bound for the potential of the nodes else, we can denote a[i] as some integer p * x + t where t is the residue modulo x , ofc t < x , (a[i] — p*x) = t , since t < x , a[i] < (p+1)*x , a[i]/(p+1) < x and p of course is greater than 1 , so x > a[i]/2 , and t < a[i]/2 so after apply the modulo operation we are basicaly dividing by two and we can do this at most log(a[i]). (The tag condition simple says that everyone is equal in the range and we can simple lazy update later)
I really doubt the first task works in nlog n Here's a test; 1,n,1,n,1,n,...,1,n i'th query is on [1,n] and makes Aj = max(Aj, i) it will be n^2
Not really. The tag condition (Max > i > second_value) will always hold for the root and we will break in it, so the complexity for such a test case is actually .
.
yup I'm wrong
So what about this?
1,n/2,n , 1, n/2 , n , ...
queries are the same as before.
You should also keep the minimum in each node (and the break condition has the case for query value < minimum). This way the complexity again will be for this case.
for this case.
I don't think you understand it completely. The segment tree goes down to nodes of size 2 for the first n/2 queries!
Yep I misunderstood the sample, but a simple fix will be to simply make the tag condition be Max > i >= second_value. This way your sample again will work in time.
time.
Why?
For the first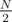 queries, the second maximum will be equal to the query value so we will stop at the root. At the second half of the queries, the second maximum will be nonexistent, i.e. it will be equal to - ∞, so we will again stop at the root.
queries, the second maximum will be equal to the query value so we will stop at the root. At the second half of the queries, the second maximum will be nonexistent, i.e. it will be equal to - ∞, so we will again stop at the root.
PS: Off course in the tag condition you should also have the case that i >= Max.
I still don't think you got what I said.
For the first n/2-1 queries the second maximum value will be n/2 and it's greater than the query value! So we will go down from root to O(n) vertices because while there is n , n/2 in this vertex we have to go down more!
Fk. I got confused about the queries (i.e. I wasn't sure if we do interval max or min). My bad.
As a whole if we do a[i] = max(a[i], V), we need to keep the minimum and second minimum. And if we do a[i] = min(a[i], V) we keep maximum and second minimum.
I think this way it explains why the complexity is good.
PS: if you use the tag condition I described in the beginning it will indeed be N^2.
I just think the whole beats segment has gone down!
Just look at this comment and you will understand why the complexity is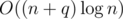 . Have in mind it's for a[i] = min(a[i], V).
. Have in mind it's for a[i] = min(a[i], V).
Dude you can see with your eyes that it runs in O(n^2)!
No :D
LOL just simulate it with the tag condition for the opposite operation and see for yourself.
A description of what will happen if you are too lazy:
Initially minimum value in the root is 1. Second minimum is n / 2.
Queries 1 -> n/2: in the root minimum is <= i < Second minimum. So the complexity is O(1).
Queries n/2 + 1 -> n: The minimum value is i-1 (=n/2 in the beginning) and second minimum is n. The tag condition i-1 <= i < n will always hold for the root so again complexity is O(1).
OPPOSITE OF MAX= i IS MIN= n-i
I'm done
I like Angel Beats.
jiry_2, I tried to write a neat code for it. I tested it with random big inputs and it passed them. I think it's correct and fast, too! Segment Beats Sample Code
Can someone has solved 453E-Little Pony and Lord Tirek explain how to appling segment tree beats into this problem ? I have tried but can't find any relation in it. Thank you in advance and sorry for my poor English :(
Can anybody help me, how can i solve the task from the article "ai = max(ai — x, 0), ai = ai + x on [l, r]", but with the queries on sum of the [l, r]?
I have doubt regarding time complexity proof of task 1. I will be considering the min(ai,b) operation.
It is mentioned that for each extra node visited we will delete one form phi(x). But, I ma finding it a little bit confusing. There might be a siutation where we have to visit O(logn) extra nodes in order to delete one node from phi(x).
For ex:- consider a segment tree with large no. of nodes. And let there exist 2 adjacent nodes in array which are very large and rest of the array values are small, clearly if we make a segment tree of this, we will have O(logn) nodes which have 1st and 2nd maximum same as those 2 adjacent nodes. and assume we have query to decrease the value of those 2 nodes, then in this case we will travel O(logn) extra steps inorder to get rid of one node which is just above last level, and for the rest of the nodes which we have traveled they may take another 1st and 2nd max value thereby not reducing the value of phi(x).
Therefore we have to perform O(logn) traversals to delete phi(x) by 1 haence time complexity will be, O(nlogn+qlogn)*logn.
If anyone is able to understand what I am saying then please help me. And it will be great if anyone can provide a better time complexity proof. Thanks
1572F - Stations is a creative problem to solve using this technique. My submission: 129343240.