Hello everyone!
I'm happy to invite you to take part in the second edition of InfO(1) Cup, an online contest meant to be similar to international olympiads such as IOI, CEOI, BOI, APIO, etc. If you remember last year's entry about the contest, you should notice that we've been talking about making it an onsite event, but we decided it's both easier (especially financially) and helpful to more people (as we can have more online participants) to have it online.
The contest consists of 2 rounds: the national round and the international round. Participation in both rounds is invitation based (you can see the "official" participants here). We've tried to reach out to the official organizers of Informatics Olympiad in several countries to make the competition as fierce as possible by having future IOI-participans, as well as to help those students in their training for upcoming international olympiads.
Both rounds will have online mirrors (which are the purpose of this entry), that you're all invited to take part in. Both online mirrors will be taken in the usaco format. The first round is similar in difficulty to a div2 contest, 5 problems in 4 hours, whereas the international round (the one meant to be similar to IOI, CEOI, etc) will last for 5 hours and participants will have 4 problems to solve. If you are a strong participant, then we advise you to take part in the international round and if not, both rounds should be a good training.
The registration button for the online mirrors will become available at the beginning of the online mirrors (keep in mind that you can choose whatever 4 or 5-hour slot you want, you'll have several days to choose from for round 2, and only one for round 1). I will update the blog with the link to the registration button as soon as possible. You can take the first online mirror during this time interval (we will keep the online mirror of round 1 after the one of round 2, and will reupdate the blog with the exact time), and the second one will start at this time and last for 72 hours. As in the case of all contests with this format, we kindly ask the participants not to discuss the problems until the end of both the official round and its online mirror (may it be the national or international round).
The online mirror of the international round is now over. You may now discuss the problems. Please give us any sort of relevant feedback in order to improve the next editions.
The online mirror of the national round (round 1) has now started. You may now choose any 4-hour frame to take it. It will end in 2 days and a half or so (better check the link). Remember that this one should be similar to a div2 in terms of difficulty, although the format is pretty different.
You can check last edition's problems and rankings here.
And last but not least, I want to present the scientific committee (in random order): I (Costin Oncescu), Alex Tatomir (one of last year's winners of InfO(1) Cup), Alexandru Niculae, Costin Tudor, Cristea Theodor











Is official registration closed? If not, what information we should provide for registering?
Theoretically yes, but as we didn't reach out to an Azerbaijan official, we could make an exception. Talk to whoever is in charge with the national selection in your country to let them know they should expect an invitation email regarding the contest, and give me (via PM) the contact information of that person. We'll send him/her an official invitation email and he/she will have to sign up the team. Afterwards, we'll send ids and passwords to the whole team. Consider, though, that we must move quickly as the contest is in 3 days and all this communication takes time.
Seeing the members of the scientific committee, I'm just curious how Romania selects IOI participants. Alex Tatomir is the winner of BOI 2017 and Info(1) Cup 2017 (I don't know if this counts), Cristea Theodor is the winner of Romanian NOI 2017, Andrei Popa is the winner of CEOI 2017, but I don't see any of them in the Romanian IOI team.
Andrei Popa has been to IOI twice — he couldn't make it till there last year (was the first one not to qualify for IOI). Alex Tatomir was in 2016 at equality with 4th position and some tie-breaker criteria was used. And Cristea Theodor won the NOI for 10th grade last year (he's 11th grade now). This is like a summary to tell more about that and confirm your information.
The competition for IOI is intense in Romania. We have the NOI which shouldn't be a really difficult contest but it does have its own difficulties (some of them related to the format and to the fact that you don't have any interface). Anyway, that is also a grade-specific contest. After you're ranked in the first half for your grade, you can participate to a selection contest 0 (which, IMO, is the most risky one for good competitors), where again, you have no feedback, but you have IOI format (3 problems 5 hours) and top 20 students among all high school grades are chosen. From here, these 20 students go through 6 more selection contests and a final ranking is formed. These 6 contests are taken in 2 separate camps. Sometimes, because the second camp is too late they are forced to consider the first one for some selections as well (for example in 2016, we had to send the BOI team by the end of the first selection camp so the most recent ranking — the one after 3 contests — was used). Aand, now from year to year the selection criteria for BOI, CEOI differ, although, it is made sure that always the better ranked has more options to choose from. The top 4 students go to IOI every year. I'll tell you what happened last year when we didn't have to choose a team earlier (as in BOI 2016): We had the final rankings, first 4 went to IOI. Then, first 8 would go to BOI or CEOI (but not both, in order to give the chance to compete and train to more students): participants were asked in order of the rankings which one they prefer (and so, in order, I chose CEOI, Constantin-Buliga Stefan chose BOI, Constantinescu Andrei-Costin chose CEOI, Tamio Nakajima chose CEOI, Andrei Popa chose CEOI, and the rest didn't have a choice (the following two were Alex Tatomir and Chichirim George with the same score, who also got first position inf BOI)). Unfortunately, being really good in Romania is not enough to assure an IOI place, although I believe that the selection is objective. The biggest risk a good contender has to miss his deserved slots to a international competition is missing that 20 people team which would mean end of the story, and because of the no feedback thing (like not even on example, you're not sure they've saved on the flash drive the correct codes) the risk is amplified. Fortunately, this was not the case for Andrei Popa or Alex Tatomir (that is why you still got to see them in some international competition representing Romania).
Can we discuss solutions of problems now?
Actually there will be an online mirror which starts soon, so I suppose discussing the solutions will happen after the end of the mirror.
That's why I'm asking.
It's written in the blog. As JustInCase mentioned, you shouldn't discuss them until the end of the online mirror (~3 days from now)
How to solve C?
We will publish the editorials after the end of the online mirror. Please do not discuss the problems until then.
Although we haven't published the editorials yet, you can find a sketch of the intended solution in this comment of atatomir.
How to solve D?
We will publish the editorials after the end of the online mirror. Please do not discuss the problems until then.
How to solve B?
We will publish the editorials after the end of the online mirror. Please do not discuss the problems until then.
Auto comment: topic has been updated by geniucos (previous revision, new revision, compare).
Results are out: http://info1cup.com/resources/InternationalPrizes.pdf
And.. I'm the first who didn't get a medal. :( Is there any chance that 110 will get a bronze, in that case you need to give 93 medals while 91 expected (182 participants total). Butthurt.
Oops, it's even 190 participants total.
Unfortunately not:( We had decided some upper bounds of how many medals we'll give when there were ~180 participants (in the meantime about 3 more unexpected teams appeared). We also chose the threshold for each medal so that the scores would slightly make sense (a 4 point distance from gold to silver, 6 point from silver to bronze, and 2 from bronze to nothing). If we gave a bronze for 110, we should give it for 109 and 108 as well, and it would lead us to 9 extra medals which already exceeds half of the number of contestants. The truth is that some of those registered didn't participate either, so it makes sense not to have really 1/2 of the number of registered users. However, I understand you, and I wish we could give more. Hopefully, next year we'll order the medals after the final rankings:)).
Also, don't forget that the medal you receive doesn't mean much: the position and score are those that matter towards your performance (after all the last gold may be closer in value to the first silver than to the first gold (not implying this is the case now), so a medal doesn't represent that much).
We're sorry for that. We still hope you enjoyed the contest.
Thanks for your reply, I understand the circumstance. Anyway, problems were really nice and interesting, they challenged me much. Hope to participate in third edition of InfO(1)Cup next year.
Congrats everyone! Tasks were great I really enjoyed solving them .. but I didn't receive the right username and password after 30 minutes from the start .. I think I could solve some easy subtasks to get silver medal but it was okay.
Last year prizes were medals not certificates .. what about this year?
Sorry for that — you were the only one who had trouble logging in. Yes, the prizes will be actual medals this year as well
Auto comment: topic has been updated by geniucos (previous revision, new revision, compare).
Solution sketches:
MaxComp: Note that the the optimal S is always a path from it's minimal element to it's maximal element. Iterate through all cells and suppose the current cell could be the maximum (if it isn't, this will result in a lower weight, so it won't influence the maximum weight). The corresponding optimal minimum can be located in any of the four quadrants around this element.
For a fixed quadrant, the optimal minimum for this element is either the element itself, or the optimal minimum of one of the two adjacent elements in the quadrant. Hence, for a fixed quadrant direction, we can process all cells in linear time if we do dp.
Del13: Denote a (in the end) destroyed neighbourhood by 0 and an undestroyed one by 1. If there are two adjacent undestroyed neighbourhood, we can't ever have chosen either of them and our moves to the left and right of them are independent, so we can split the problem whenever we see 11. This way we reduce to the case where there are some isolated ones separated by blocks of zeros.
For the reduces case, in our move sequence we'll first choose some cities inside the blocks of zeroes and then choose some of our ones some number of time. If a one is chosen more than three times, we could instead have chosen it two times less and choose an additional city inside each of the adjacent blocks of zeroes. Hence every one is chosen at most three times and we can do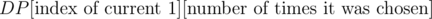 to solve the problem in linear time.
to solve the problem in linear time.
Hidden Sequence: First query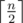 ones to figure out, whether there are more ones or zeros in our sequence. W.l.o.g let there be more ones. We now want to get the number of zeros between each pair of adjacent ones. At any moment, out state look like 10?1?1101 where a ? marks some non-negative number of zeros. If at any moment there is at most one ? left, we put all zeros into its blocks.
ones to figure out, whether there are more ones or zeros in our sequence. W.l.o.g let there be more ones. We now want to get the number of zeros between each pair of adjacent ones. At any moment, out state look like 10?1?1101 where a ? marks some non-negative number of zeros. If at any moment there is at most one ? left, we put all zeros into its blocks.
In a single step, we can pick some ? and query: "ones to the left of it + zeroes in the block + one more zero + ones to the right of it". If the query succeeds, add one more zero to the block, otherwise remove the ?. If we alternate expanding the blocks, we do at most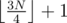 queries, which scores 69 points.
queries, which scores 69 points.
To get more points we can do some dp to find shorter sequences matching the parts to the left and to the right of the current block. If you alternate expanding blocks, you score 95 (In theory only 87, but you'll get lucky.) and if you pick an optimal block at every step, you score 100. Does anyone have a proof why this never does queries longer than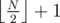 ??
??
Balanced Tree: Do a binary search for the answer. Now do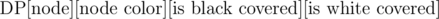
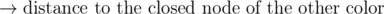 . In the transition, you need to check whether the nodes of equal color are close enough to cover each other and remove states where a node gets the wrong color or the node of the other color is uncovered and to far away. This runs in
. In the transition, you need to check whether the nodes of equal color are close enough to cover each other and remove states where a node gets the wrong color or the node of the other color is uncovered and to far away. This runs in 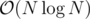 and scores 94.
and scores 94.
To get 100, compute the distance to the closest node not having a different color for every colored node in by some all-directions dp. Pick the the maximum, use it as a lower bound and set the upper bound some small constant higher (Four works, but I think one suffices. This idea on its own can be used to score some points in the fourth subtask.). This reduces the runtime to
by some all-directions dp. Pick the the maximum, use it as a lower bound and set the upper bound some small constant higher (Four works, but I think one suffices. This idea on its own can be used to score some points in the fourth subtask.). This reduces the runtime to  and scores 100.
and scores 100.
So I guess all my solutions involve dynamic programming...
Can you please explain in more details your optimisation on third problem? I don't get how you shrink the length to at most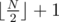 .
.
UPD. Got it in the comment below.
Hello dacin21 ! First of all, congratulations on your result ! Thank you for your sketches. Your solutions are very similar to ours. Regarding the proof of [N / 2] + 1, I will give a fast explanation. We try to find the position of every 1 in the hidden sequence.
Let's say that you want to find the position of a '1'. It has a zeros and b ones to the left. It also has c zeros and d ones to the right. We want to be able to do one of the following final queries:
We also know that a + b + c + d equals N — 1. Hence, at least one of the queries is at most [N / 2] + 1. We add zeroes progressively until the sequence does not exist or we exceeded the limit. If we exceeded the limit in both parts, then both queries are final and any additional zero would lead to a 'false' answer.
Regarding "Balanced Tree", there are only two 2 contestants who solved it during the online mirror. Radewoosh solved it in the 5-hours period while you up-solved it. Congrats ! I am very glad that you found the same solution as us. I also invite anybody with different approaches (even for the chain/path subtask) to share their solution with us.
An official editorial will be posted on the website in the following days. I hope that all of you found at least one interesting problem during this contest. Feel free to give any relevant feedback so that we will improve the quality next year.
Also, as a completion of atatomir's comment, I wanted to add that in balanced tree, in the assessment part, you need at least a +2 (we have tests that require that, but only when the search interval is [1, 3] instead of [1, 2]). We could only prove +3 upper bound.
As for the dp part, unfortunately your solution was not the intended one (ours doesn't use dp in any way) and I'm not sure whether it's correct or not.
Judging by the ellipsis mark in your last sentence, I feel that we've let you down:( Still, we only wanted 2 of the problems to require dp (second and forth) as for the first one we considered partial minimum/maximum not to be a dp and third problem seemed impossible to approach by using dp (I'm still stunned that you did so and succeed). The second one also had an alternative greedy from what I could see in people's solutions, but the intended solution was dynamic programming as it was easier to think and to code. I genuinely think and hope that this year's edition was better than last one and that we're in a continuous improvement. Hope you've still enjoyed the contest and we hope to see you as a participant next year as well:)
Thanks for the comment. Intuitively I thought + 1 would be enough, but now I found a case requiring + 2. (I just took the + 4 based on the subtask scoring.)
Your solution for hidden sequence is a lot nicer than mine (I might try to proof some upper-bound for my solution tomorrow.). I really liked this task, even more so after seeing your solution. The thought behind my solution was that exploring the blocks of zeros worked well for some subtask and if there is some solution in that direction, my dp will find it.
I also liked the last problem, the solution wasn't so obvious at first glance (It took me a few hours of upsolving until I found the correct idea.). My initial DP didn't work, so I search for some binary-search + 2SAT solution, but I didn't find any. I was really happy when the dp transition worked out in the end.
My last line was mostly some random comment to myself (I tend to use dp quite often, maybe to often.), my solutions still required some specific observations and I liked the overall difficulty. I'll definitely be participating next year.
Thank you for the feedback!
I'm glad to hear that you've enjoyed the problems. I feel you about the dp (I may use it too often too), but I guess that as long as some nice observations are behind it, it doesn't really matter.
Also, I'm happy to see that our ways of thinking were similar (I've also tried something with 2sat at some point and your solution is the exact official solution:)) ).
Also forgot to say thank you for publishing a sketch editorial — this might help people get going with the upsolving before we get to publish the editorials
I have a greedy solution for Del13
First, define d[i] = p[i] - p[i - 1] - 1 (consider there's a city #0 and a city #n+1). The problem asks to do one of these operations: choose some i and subtract one from d[i] and d[i - 1] or subtract 2 from d[i] if d[i] > 2. The problem is that d[i] must be "fixed" which means 1 or 2 should be subtracted from it using the first operation depending on its parity (because after reducing it by 2 several time using the second operation it will end up as 2 or 1 and you must go with the first operation).
Let's loop over d[i]. If it's odd, the only way to "fix" it is to subtract 1 from it and from d[i + 1]. If after the loop there's still an odd d[i], no solution. Now we're left with some even numbers and some of them are fixed. Let's define a connected component as a subarray [l;r] with non-zero elements such that d[l - 1] and d[r + 1] are zero (or out of bounds). We'll fix every connected component. If its size is even, fix every pair. Otherwise you must find an odd index with d[i] > 2 and fix it twice or d[i] is already fixed and skip it. If you can't, no solution. Now as every element is fixed you can just reduce all positive elements by 2s (put these operations first).
Can you please leave server open for another week, so we can upsolve problems?
With great help from the organizers, you can submit ALL problems from the international round right now: https://oj.uz/problems/source/321
Thank you very much.
Can someone please tell me solutions for problems Scoica and Cambridge from National round?
Where can we find problems of National Round?
I don't know but I kept Scoica and Cambridge.
Here is link to problem statements: https://drive.google.com/drive/folders/1qBxUSTBGsog3H18ZVVyOZ1PRtm_9ZVKl?usp=sharing
With great help from the organizers, you can submit ALL problems from the national round right here: https://oj.uz/problems/source/322
For scoica you will use two dp's. To do that, you will run a dfs on the graph and you will practically go through the p nodes in reverse order. Let's note the list of the p nodes with S. dp[node]= the index in S of the last node (in reverse order) from S from the path from N to node. I.e. if the node is 5, N is 9, the path from 5 to 9 is 5 8 6 9 and the p nodes from S are 2 3 8 6, dp[5] will be 3 (value 8) because the last node (in reverse order) from the path from 5 to 9 is 8 (6 is the first one in reverse order). Also let nr[node]=the number of paths from node to N for which dp[node] has that value.
For each son of node you will have the following relations:
if (dp[son]<dp[node]) dp[node]=dp[son], nr[node]=1; else if (dp[son]==dp[node]) nr[node]+=nr[son];
Also, afterwards, if node is equal with S[dp[node]-1], decrease dp[node].
Finally, you will print nr[1].
I got a bit different idea. If we must visit nodes 1, p1, p2, ..., pk and n, then we compute number of ways to come from pi to pi + 1. At the end we just multiply all of them together. To get number of paths between x and y I used the following algorithm. We first reverse all the edges. And then we do some kind of topological sort. We remove y and then add nodes which have in-degree 0. We repeat this procedure as long as possible.
dp[a] means number of paths from y to a.
dp[y] = 1
dp[a] = dp[f1] + dp[f2] + ... d[fr] where fi is a father of a (there is a directed edge from fi to a).
Can someone please tell me if this algorithm is correct? If it is not, please provide me a counterexample (regarding time limit or correctness itself).
For Cambridge, firstly, for an interval [p,q], you should sort the problems by their D. Why? Try to swap two of them after you sort all of them and you will see that if you cannot satisfy the condition when they are sorted, you also cannot satisfy the condition when you break their order by swapping two of them. So optimally, you should sort them by their D. To do this fast, you should use two pointers: i and j (i<=j). You go through the problems increasing the j while you can. By this, I mean that you should increase j as much as possible while the condition is satisfied for [i,j]. When you cannot increase j anymore, increase i until the condition is satisfied again. This has O(n) complexity and you will now that way for each j how much you can go to its left so that the condition is satisfied and answer the queries in O(1) each query. Now, how to check if the condition is satisfied? Use a segement tree. If values for D were below 10^6 each time you increase the j, you should update the segment tree with -T[j] on the interval [D[j],10^6]. When you increase the i, you should update the segment tree with T[i] on the interval [D[i],10^6]. Also as soon as you meet one D[j] on your way, the first thing you have to do is update the interval [D[j],D[j]] with D[j]. (Because later you will decrease this value with those Ts). If one value from the segment tree becomes negative at one moment, then the condition is not satisfied anymore. Now because Ds are below 10^9, you can either use normalisation, or a dynamic allocated segment tree.
Thank you very much. I got the same solution but I wasn't sure about increasing D property.
Why official editorials have not been published yet?