242A - Heads or Tails
This problem was very easy, we should only use two cycles with i and with j (a ≤ i ≤ x, b ≤ j ≤ y), iterate all possible outcomes of the game and print such in that i > j. The time is O(x·y).
242B - Big Segment
At first, we must note that the answer is always unique, because if segment i covers segment j, that segment j can't cover segment i. It possible if and only if there are coincide segments in the set, but it's not permissible by the statement. Let's pay attention the answer covers the most left point of all segments and the most right point of all points too. Now then we should found L = min(li) and R = max(ri) and print index of segment [L, R], or - 1 if there is no such segment in the set. The time is O(n).
242C - King's Path
The most important thing for accepted solution is that it is guaranteed that the total length of all given segments doesn't exceed 105. We should use this feature, let's number allowed cells and found shortest path by BFS. It's easiest to use associative array such as map in C++ for numbering. The time is O(n·log(n)).
242D - Dispute
Denote current value of counter number i as bi. Let's describe an algorithm. It takes any counter i such that bi = ai and presses its button. The algorithm finishes if there is no such i.
Let's proof correctness of the algorithm:
Why does Valera win the game? Because there is no such counter which has bi = ai else we must press the button.
Why doesn't algorithm press some button multiple times? Because it presses button number i only if bi = ai, and after this pressing the value bi is increased and the equation will be true never.
Why is the algorithm fast? Because of paragraph 2 it does no more n pressings which produces no more n + 2·m increases of the counters. We should use queue for fast seaching counters which has bi = ai like this: every time we change value of the counter numbered i we check equation bi = ai and if it's true then we push value i to the queue. It's easy to understand that all indexes i will be in queue no more one time.
Also these paragraphs proof that the answer always exists. You must print - 1 never. The time is O(n + m).
242E - XOR on Segment
Let's write numbers a1, a2, ..., an as a table which has size n × 20, and bi, j is jth bit in ai. Then sum of numbers on segment [l, r] equals 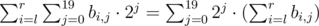 . The last notation helps us to process queries.
. The last notation helps us to process queries.
For fast implementation we should use 20 binary trees like cartesian trees or range trees. Every tree matchs one of bits (and matchs one of the columns of the table bi, j).
calculation of sum is equal to counting 1-s from l-th to r-th.
operation "xor" equals reversing all bits from l-th to r-th (i.e. 0 changes to 1, 1 changes to 0).
The first operation executes for all bit numbers, the second executes only for bits in which input number xi has ones.
These operations may be easy implemented with binary trees. The time is O(m·log(n)·20).











Excuse me ~ Can you write a solution in English ?~^。^ I'm very impressed with your E problem and want to learn it for a lot.But I can not read Russian. So ……~~
goto this link:
http://codeforces.com/blog/entry/5837
Thanks a lot ~ ^_^
In problem E complexity should be O(n) + O(m*log(n)*20) = O(n + m*log(n)). Isn't it?
No, that is not how you calculate the sum of terms in Big-O-Notation. The correct way in this case is to take the fastest growing term, which is O(m*log(n)*20). You can read more about the Big-O-Notation for example in Wikipedia: http://en.wikipedia.org/wiki/Big_O_notation , which will tell you the following: "If a function f(n) can be written as a finite sum of other functions, then the fastest growing one determines the order of f(n)."
Why do you think that m grows faster than n in this case?
Codeforces editorials rarely give detailed explanation of the harder problems, especially when the problem is just about using an advanced data structure. The editorial just says "This can be done using interval trees.". Can someone please explain how to use segment trees in Problem E in more detail? Your explanation will be useful for all those who are just starting to learn segment trees, thanks!
check my code. 2559296
if you dont understand any of my code, please let me know.. :)
thanks for sharing your code
i understand the build function and a bit of the query and update function. can you explain what is the lazy array used for?
From looking at the code I think it is "Lazy Propagation". Search that up
I recommend that you first solve https://www.codechef.com/problems/FLIPCOIN to learn about lazy propagation with Segment tress and then solve E problem.
My solution http://codeforces.com/contest/242/submission/17871914
pro E: nx20 ??why??thanks...
because 2^20 > 1000000 so 20 bits is enough to represent every number
Really, we would really appreciate if someone could give a detailed explanation on the solution of E using segment trees. Thank you.
I think The time is O(n+m) for 242D — Dispute
I solved 242E — XOR on Segment with naive algorithm without using any data structer
look at my code it solved the problem exactly on time limit and got accepted
lol :D :D how did that code pass tests ?
4000ms!!!
Yes, one more 1ms and my code will get Time limit exeeded
This naive solution may be a little bit optimised.
Instead of using count — just check that tmp is far from overflow.
Compare solutions 3064707 and 3064734.
I_love_Tanya_Romanova, Can we solve it using fenwick tree. If no, why not ? I read some blog that we can do range update + range query using fenwick tree, but could not solve this problem using this concept. Note that I'm clear with the segtree lazy propag. solution idea.
I solved this problem using segment tree I am getting WA on the 15 th test case can anyone help me finding bug in my code here is the link https://ideone.com/0OuZRq
I am also getting WA on test 15
can anyone please point out what is wrong with my code?here is my code http://codeforces.com/submissions/vis10326#
Clean your code first. Put some spaces and indentations would be enough
http://codeforces.com/contest/242/submission/9527768 and http://codeforces.com/contest/242/submission/2563497
The same code...i m not as lucky as the latter.
I am getting wrong answer on test 10 in problem C My code: http://codeforces.com/contest/242/submission/14186492 anyone please help
Same problem, In fact I am also getting the same answer as yours for test case 10 :/
E : good problem
So much week testcases of problem E. Many of accepted solutions have more than 10^5 * 10^5 complexity.
lazy segment tree solution of E Xor On Segmentcode
Can anybody explain E ? Thanks.
If you are still curious about this problem — the idea is as follows. Maintain a segment tree for each bit and a lazy tree for each bit (containing info on whether ith bit is set in each of the numbers). For each update query, flip the bits in the current range and invert the child's lazy bit values, but only if the ith bit is set in the number that we xor our range with, otherwise skip to the next one. The same is applied in the sum query.
It is the standard lazy segment tree implementation with a little twist (multiple trees). Here's a link to a tutorial and my submission for further clarification:
https://codeforces.com/contest/242/submission/103977271
https://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/
Is it also rated for division 3?
can't we solve problem E with lazy-segment tree? thank you in advance..
Yes all we have to do is to construct 20 lazy segment tree for every bit.
my solution: 216845895
How is the time complexity of problem D is O(nlog(n))?