A. Will he Die?
Vendetta. solution: https://ideone.com/N8WC9O
justHusam solution: https://ideone.com/oAPb42
Complexity: O(N) for pre-calculating factorials and 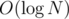 per test case for the multiplicative inverse.
per test case for the multiplicative inverse.
B. Ran and the Lock Code
Vendetta. solution: https://ideone.com/VNyo8h
justHusam solution: https://ideone.com/KChjCF
Complexity: 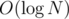 per test case.
per test case.
C. Professor Agasa Lab
Vendetta. solution: https://ideone.com/Vz5u8p
Complexity: 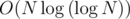 for pre-calculating totient and O(1) per test case.
for pre-calculating totient and O(1) per test case.
justHusam solution 1: https://ideone.com/yXLv7v
justHusam solution 2: https://ideone.com/s4EdLm
D. Help Conan
Vendetta. solution: https://ideone.com/g6gcKd
Complexity: O(2N × N) per test case.
Complexity: O(2N × M) for the other slower solution per test case.
justHusam solution: https://ideone.com/uXfZUV (A bit different solution)
E. Rescue Haibara
Vendetta. solution: https://ideone.com/bF0axw
justHusam solution: https://ideone.com/LxK1PD
Complexity: O(N) per test case.
F. Median and Queries
Vendetta. solution: https://ideone.com/3EZ1SY
Complexity: per test case: O(N2 × Max(Ai)) for construction and O(Max(Ai)) per query.
justHusam solution: https://ideone.com/WEkeVH
Complexity: per test case: O(N2 × Max(Ai)) for construction and  per query.
per query.
G. Preparing for Exams
Vendetta. solution: https://ideone.com/yKYgb9
justHusam solution 1: https://ideone.com/u8xofZ
justHusam solution 2: https://ideone.com/XNvyX9
Complexity: 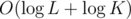 per test case since sqrt(x) complexity is
per test case since sqrt(x) complexity is  .
.
H. Genta Game
Vendetta. solution: https://ideone.com/C6X94O
justHusam solution: https://ideone.com/YYrF7f
Complexity: O(1) per query.
I. UEFA Champions League
Vendetta. solution: https://ideone.com/NWtBvZ
justHusam solution: https://ideone.com/c7m35z
Complexity: O(1) per test case.
J. Gin Passwords
Vendetta. solution: https://ideone.com/bLV0UI
Complexity: O(Max(gn)) per test case where gn is the nth prime gap.
K. Conan and Scoreboard
Vendetta. solution: https://ideone.com/0bLR7c
Complexity: 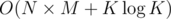 per test case.
per test case.
justHusam solution: https://ideone.com/aBKduB
Complexity: 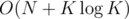 per test case.
per test case.



 and Left with probability
and Left with probability 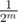 as we have
as we have 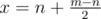 . Now the probability will be
. Now the probability will be  where
where 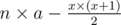 which will be distributed on
which will be distributed on 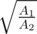 , from which we can find
, from which we can find 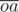 and
and 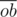 then
then 






Auto comment: topic has been updated by Vendetta. (previous revision, new revision, compare).
Why is the following approach wrong for problem D. Help Conan?
1) Let d(i, j) denote the shortest path between two nodes i and j in the original graph.
2) Build a new weighted graph consisting of only important nodes and weight between two nodes i and j to be d(i, j).
3) Find MST of this new graph.
That is an interesting solution, unfortunately it fails in cases like this:
Consider 2, 3 and 4 to be important, the new shortest paths will be:
2 3 2
3 4 2
2 4 2
MST for that is to take any 2 edges which will be of cost 4, but if you take all the original edges in the graph the cost is 3.
The problem with this solution is you take same edges multiple times, thus get more than the optimal solution.
I think, with the problem B, we just calculate the min((a-1)*2 + 1, n) if a <= (10^9)/2 else we calculate the min((10^9-a)*2 + 1, n) ?? So that is O(1) solution.
Does that work with the test cases?
It will fail on this case:
10 3becausemin((3-1)*2+1, 10)is5.But the optimal solution is
6, example:1 2 3 4 5 6 1 1 1 6.Hi Vendetta! Would you mind sharing test data for "A. Will he Die?"? I hit Runtime Error on server, but locally code works just fine (I even ran test with all possible inputs, -2e5 <= n <= 2e5, 0 <= m <= 2e5. Approach basically same like in editorials, except that instead of calculation of modulo inverse through Euler's totient function I used extended Euler's algorithm.
I just read your comment sorry for the late response, you are using arrays of size 2 × 104 instead of 2 × 105, thus you access memory out of the array which is leading to Run Time Error.