I participated ACM-ICPC World Finals in 2017 and 2018, and I am trying to coach people who are willing to compete ACM-ICPC.
As a participant and educator, I always wondered that "Why there are no syllabus in ACM-ICPC?" IOI has their syllabus. It changes from year to year, but it is least guideline that how can you ready for the competition. For example, 'non-trivial calculations on floating point numbers, manipluating precision errors' is excluded in IOI, so I did not practiced about real precision error deeply (but did in ACM-ICPC, since some problem requires it). Actually handling real numbers in computer is complicated, same recursion formula can earn different result, etc,. You can think about following problem: "Determine whether 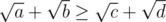 for integer a, b, c, d." Double precision cannot help you when each number is 5 digit.
for integer a, b, c, d." Double precision cannot help you when each number is 5 digit.
Which area you should concentrate on practicing ACM-ICPC or other programming contests? Even well-known part in programming contest is not covered by undergraduate (at least school where I am, Computation Geometry, Graph Theory is for Master's degree.) and some is not covered by even graduate education. You might know about impartial game and Sprague-Grundy theorem about impartial game. Game theory is one of topic for Senior and Graduate student in departure of Mathematics, and the class did not handle about impartial game.
Moreover, do we really have to know about Physics (Newton's laws of motion, Optics, etc,.) while programming? You do when you have to write some simulation program for physics lab or class but really in participating ACM-ICPC or other programming contest? Does it really help us for testing competitive programming skills?
Actually, I am writing this because I am writing a book titled "Mathematics for programming contest." and I have no idea about which area should I write about. I am considering even writing about Matroid theory and Generating function.
I hope programming contest concentrate on algorithmic thinking, not prior knowledge of harsh area. So I have a question. Why there are no syllabus in ACM-ICPC?











I think In such cases usually all needed formulas and constants are given and you don't really need to know physics (though it might help with intuition), in which case it's not much different from other mathematical problems (either on geometry, number theory or some calculus).
I hoped so, actually it wasn't. One of my teammate had hard time finding formula on 2018WF problem E
Problem F from 2016 ACM ICPC Asia Nha Trang Regional is literally a physic problem, and while the problem statement mentioned Archimedes’ principle, the principle itself is not stated in the problem statement.
Square it a couple of times with larger size integers, I guess...
Actually you can, because sqrt(a)+sqrt(b)-sqrt(c)-sqrt(d) is algebraic number, you can calculate minimal polynomial (over Q) and check.
Anyway, imagine this kind of problem came out as Div1A, many of them submit and fails on system test and author says so
I think that the main reason why there is no syllabus is that it is not so obvious that there should be. It's not even clear whether a topic is hard to come up with using no special knowledge. For example, in the wf's problem E it seems straightforward to me that once horizontal speed is constant and vertical speed is linear over time, the trajectory is parabolic. It's so not because it's known from a physics course, but because a primitive of a linear function is quadratic.
Moreover, if you write a list of what a wf problemset should or shouldn't consist of and why, you have to convince the problemsetters committee that your changes won't turn a working system into something that is supposed to be very nice but in fact is like the new gcj platform.
OK, think about following problem:
Is there a stable compound consists of c Carbons and h Hydrogen? Print 'Yes' or 'No'. (1 ≤ c, h ≤ 10)
This problem is solvable, if you know about Valance Bond Theory, but is this problem really for programming contest?
Or this problem:
There is topology (X, T) where X has n elements, from 1 to n. Find the number of open sets of T where subbase consist of m elements of topological space is given. (1 ≤ n, m ≤ 20)
This problem is also solvable, rather this is more formal than previous one. This is problem even using bitmask. Good implementation problem, huh?
I really do not know what ACM-ICPC or other programming contests requires to us. There should be guideline we can follow, not by deduction that "Oh, there was such problem in World finals before so similar problem can be in problemset of this year!"
I agree that every problem statement must be explained in a very clear way. I have never seen a task with a sentence "the roadmap of Berland is a tree" and at the same time without an explanation like "that is, there is the only path between two arbitrary cities". I think that it's the highest priority side of a statement to be clear for everyone. I believe that each contest is not a statement parsing contest, and understanding a statement must not increase the complexity of task by any single bit. For the same purpose many mathematicians, including Terence Tao, write their articles in such a way that at every moment the reader knows what is going on, operating at the same time with some advanced concepts.
Your two example tasks don't obey this rule. I don't remember exactly, but I believe that E from wf contained a description of a formal model of the motion.
In my opinion it's more a how-to-write-a-statement rule rather than a syllabus.
Then, what can be written or not without explanation? IOI syllabus states it. It is least required knowledge for competition.
Ok, now I got the essence of your question. Well, at the moment, I believe, there can't be any, and one can expect anything in a wf problemset, eg a task on the simplex method, a task on parsing the statement and figuring out what is going on, a task on squeezing into tl or a task on obtaining an exponent of a polynomial in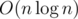 (didn't see the last two types of task in a wf problemset, though). I am not sure if it's good or bad, that's just it, a wf's format.
(didn't see the last two types of task in a wf problemset, though). I am not sure if it's good or bad, that's just it, a wf's format.
Do you really think that all tricks and theorems that can be useful on programming competitions should be taught in typical unversity courses? Most prestigious competitions (like IMO/ACM) always had their own rules and can include anything that organizers consider as reasonable.
Regarding physics, I don't know about this year's problems (and please do not tell me about them), but ACM ICPC WF 2006 featured a really tough problem that I wrote about here: http://codeforces.com/blog/entry/51796 which I think requires really good physics understanding. It seems that it required even better physics understandings than one that author of model solution had (at least that solution on ejudge which is not an official solution), because it failed a cube case which I wrote about there. But it was 12 years ago, I think that you should not deduce anything about current fashion from this.
No they are not. Then why bother telling us?
I usually joked with teammates that every knowledge human knows is syllabus. And now, I am not joking.
I never felt a need of having some syllabus to any contest I participate in and "all humankind's knowledge that seems reasonable for this particular contest" is fine for me and not funny.
Who can decide that "seems reasonable" part in every contest? For example, whether physics is reasonable or not to be in competitive programming seems to be debatable among countries, according to recent discussions. In this condition, "All humankind's knowledge" is just a fake, it should be written as "All knowledge from problemsetter and his community".
During a programming contest, I personally am happy to be at the mercy of the problemsetter and whatever they choose to put on the contest.
I also respect problemsetters and their problems. But when it comes to very huge and important contests, at least various problemsetters from various countries should have some consensus to choose topics. It would feel very unfair if some problem was from Korean 2016 paper and only one team saw it could get AC.
I remember myself posing a problem which requires heavy prior knowledge to David Bowie’s discography, although I made it lenient by giving strong samples.
problem
Personally I oppose to the idea of “syllabus”, as it limits the scope of ICPC. But if people keep posing a problem that could be “unreasonable” to some, then maybe we don’t deserve that right. I also cite GP of Gomel’s problem J, as the problem that is reasonable to some people.
Is this problem available in English? Samples are indeed strong but still unsufficient to under what's going on :)
Problem: For each query S E, print all of the David Bowie's discography from year S to year E.
Actually there are all of them in 2nd example, so you don't need to search it in google :)
My favourite physics problem is D from GP of Saratov two years ago.
How is your military life?
Wow, is he in the military? He is not only good at programming but also in fighting. What a super soldier!
South Korea has compulsory military service.