Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | jiangly | 3578 |
| 4 | orzdevinwang | 3570 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | tourist | 3565 |
| 8 | maroonrk | 3531 |
| 9 | Radewoosh | 3521 |
| 10 | Um_nik | 3482 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
| Name |
|---|



I asked someone to explain my div1B solution to me in this comment
And you actually did that, thanks :D.
SirShokoladina please fix div2E. There is parsing error.
A lot of things to learn...
C shows up as "unable to parse markup" for me.
thanks for noticing! it should work now
Can you please provide code to the solutions, especially Div 2D/1B... really hard to understand the solution for me. Thanks a lot
Also, Div 2E/1C problem is missing it's solution
Here is my code for second solution for div1B:
https://pastebin.com/FpfJXVH0
Here is the first solution for div1C:
https://pastebin.com/2KemU4bN
Here is div1E, but here z = 0 means that there were people on stations and z = 1 means there were no people.
https://pastebin.com/5ZdKuRkM
I don't understand div2 C part where it says that answer can be no more than n-x. Can somebody explain me little bit better?
I think there is some inaccuracy. Consider cycle and every element in it: break it on intervals between elements equal to concerned element (include first boundary, exclude second). When element is single there is one such interval. Obviously that on every interval there is exists at least one bad replacement. So in every cycle at least k bad replacements, where k is max number equal elements in cycle. So if there is x equal elements in array then in every partition on cycles there is at least x bad replacements.
how is it obvious that there is one bad replacement on each interval, why cant all elements be good replacements for some particular interval of some cycle ?
Because we start and end on same value. Try to move ahead with this thought.
Okay, that's pretty clear now, thanks !!
Great Contest! With mind blowing problems. SirShokoladina Sir, you should conduct contests more often.
LOL I did some kind of precalc on div1B. 40296044. My solution has complexity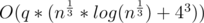 . But I can't implement it without map which contains vectors so it is very slow. Then i noticed that it can be precalculated and instead of 43 * log with bad constant it gives clear 43.
. But I can't implement it without map which contains vectors so it is very slow. Then i noticed that it can be precalculated and instead of 43 * log with bad constant it gives clear 43.
I think for the second solution to C, you mean to say that X and Y are the minimal possible values satisfying that condition (but the solution works).
Yes, fixed it.
Overall, I thought the logistics of the contest could have been managed better. Some of the problem statements could have been worded better, there were a lot of clarification announcements, etc.
That being said, I thought the problem quality was good, especially Div 1 C. If Div 1 BC were shifted down 1 problem (can't speak towards D or E), and another Div 1 B made, I think the problem scaling would have been perfect.
Can't understand the second solution for Div1.B. The solution says:
"In such way every satisfying this criteria parallelepiped (not considering the orientation) with three different side lengths was counted 6 times."
Let's consider the large parallelepiped to be 4x6x10, the small parallelepiped 2x3x5 will only be counted once. Why the solution says that it is counted 6 times?
(Actually, can't understand the first solution either... What does "mask" mean in the solution?)
we count it 6 times — as 2x3x5, as 2x5x3, as 3x2x5, as 3x5x2, as 5x2x3 and as 5x3x2
mask of length 3 in a subset of set {1, 2, 3} written as a 3-digit binary number. so 0 = 000 = {}, 1 = 001 = {1}, 2 = 010 = {2}, 3 = 011 = {1, 2}, 4 = 100 = {3}, 5 = 101 = {1, 3}, 6 = 110 = {2, 3}, 7 = 111 = {1, 2, 3},
But the direction of the large parallelepiped is fixed, and 3 is not a divisor of 4, so why is 3x2x5 counted?
Because we use the IEP on rotations (permutations), so both 2x3x5 and 2x5x3 are rotated in all directions and if at least one orientation satisfies then it is counted once, otherwise it is not counted.
so my understanding of div2D was correct but problem statement and number of submissions prevented me,huh,sad
can anyone help fix my mistake for div2 B?
Submission Link
x > curh and y <= curh it will not update curh, in fact, curh = y.
?detaR tI sI
Why did my code of div1C which used "exit(0);" get "Idleness Limit Exceeded" in pretest 12?
you noob
kappa
maybe you use "exit(0)" before you actually guess the correct numbers?
Oh I found a precision error in my code. But when I changed "exit" into "return" it got accepted.
can you show me your code?
exit:http://codeforces.com/contest/1007/submission/40288030
return:http://codeforces.com/contest/1007/submission/40303376
seems like the codes are really equivalent... I don't know, maybe you have ub.
Can Someone Please tell me a more intuitive way to understand the solution of div2 C (div1 A) or different easier approach if possible???
The problem can be done by using two pointers. Lets sort the given array and initialize count and both pointer to 0. say pointers be i and j. starting from index 0, take next biggest element(by changing j) and when you find that, increase i, j and count. Here we are calculating the possible number of pairs in which smaller can be replaced by bigger number. Here is snipped for what I did:
Can someone please elaborate on the Div1B Second solution? (The Inclusion exclusion one) ...?!
It is not very clear to me how the "ans2" part is calculated by the author's solution...
If you had a different combinatorial solution please share that as well ..
ans2 supposes that the first two lengths of the parallelepiped coincide. That means that this length should divide two chosen dimensions of the big parallelepiped. thus we use g[x[0] | x[1]]
Look at my other comment lower, maybe it will help.
thankyou , the whole approach is still exotic to me as I have never seen something like this before, but get your solution..
It seems that SirShokoladina forgot to link the editorial to the problems in Div2 (contest 1008). In any of the five problems we can't see the link of editorial.
I don't know how to link them. I guess Codeforces this automatically.
I'm sorry... I don't know that before.
You can do that by clicking clip image at the top of the blog
Can anyone explain div2d in understandable way?
I can elaborate on the second solution. First, google what inclusion-exclusion principle is. I'll explain its meaning. Assume you have a bunch of sets and want to know the size of their union. If for every set of this sets (for example "1st 2nd and 4th set" or "3rd and 5th set") you know the size of their intersection then you can count the size of their union.
We have six orientations. Each of them gives us a set of parallelepipeds that we can pave the big one with. One of such sets is "1st side divides the 2nd side of the big, 2nd side divides the 1st side of the big and 3rd side divides the 3rd" side of the big", let's mark it 213. Now how can we find the size of intersection of several such sets? If we had two permutations 132 and 231 then a parallelepiped is inside the intersection of their sets if it satisfies both orientations. So its 1st side must divide both 1st and 2nd sides of the big, 2nd divides the 3rd side and 3rd divides also both 1st and 2nd. Then there are #d(gcd(A, B)) * #d(C) * #d(gcd(A, B)) such parallelepipeds (where #d is number of divisors). So we know the size of every intersection, thus we know the size of the union, which is the number of parallelepipeds that we can orientate somehow so it can pave the big. But now 2x3x5 and 3x2x5 are both counted. That's why we need to count something more, read the tutorial and I will continue if you don't understand.
I understand to your part. Can you elaborate more? I mean, I know the inc-exc principle (union of a,b,c is a+b+c-ab-bc-ca+abc etc.) but I dont understand the editorial having read it 5 times already xD
Maybe its just simple language but yours seem much more clear. Cant understand a single word from both solutions :P im bad at math lol Also, what do u mean about 2x3x5 and 3x2x5 being counted multiple times sir
So for one query we perform following algorithm: use exc-inc principle for all 6 permutations (1,2,3) and count intersections of each subset of sets so we can obtain the union of this permutations which is our answear am i right? Second question is what does exactly p(m) from the end of the editorial mean, i dont get it ;(
You were right in the beginning, but that is not exactly our answer. This is the answer, but when 1x2x3 is counted 6 times (as 1x2x3, 1x3x2, 2x1x3, 2x3x1, 3x1x2 and 3x2x1), 1x1x2 is counted three times (1x1x2, 1x2x1 and 2x1x1) and 1x1x1 is counted once.
So the second number we count will be the same, but considering only parallelepipeds XxXxY, so two first sides coincide. Assume we fixed a set of sets and found which sides each side of the small parallelepiped must divide. In my example it was (A, B), (C), (A, B). Now as we know that first two sides are equal, we must unite the first two sets, so it will become: (A, B, C), (A, B, C), (A, B). So the number of such parallelepipeds will be #(gcd(A, B, C)) * #(gcd(A, B, C)) * #(gcd(A, B)).
In the second number 1x2x3 was not counted (as 1 != 2), 1x1x2 was counted once (1x2x1 and 2x1x1 are not counted as 1 != 2) and 1x1x1 was counted also once.
We multiply the second number by three and add it to the first. Now 1x2x3 is counted 6 times, 1x1x2 is counted 6 times and 1x1x1 is counted 4 times. Now we add #d(gcd(A, B, C)) * 2 and everything is counted 6 times. Then divide by 6 and get the answer.
So we do count the second number exactly the same as the first one but on each intersection we consider first two sides to be equal? We use inc-exc principle once again right?
Right.
And what did p(m) meant on the end od the tutorial on this task? (In time comlexity).
https://en.m.wikipedia.org/wiki/Partition_(number_theory) in case of m=3, p(m)=3: 1+1+1 (three unequal lengths), 2+1 (two equal lengths and one more), 3 (the equal lengths)
Last question.In counting second number we can assume that first and second are the same because of symmetry, right?
yes
Thanks for help both of you guys. I appreciate it.
For div2C does cycle decomposition work if the permutation contains repeated elements? I mean for the proof it is assumed that there is a cycle decomposition?
Permutation can't contain equal elements
Haha, I have a passing O(number of divisors * constant) solution of div1B. It's only barely passing though.
We can build bitmasks for each divisor describing which input numbers it divides. The key is that for each triple of bitmasks corresponding to the smallest, middle and largest number, we can pick an arbitrary assignment of dimensions to these three bitmasks (or ordering of three chosen divisors). Then, for each query and each ordering of divisors (6 in total), we can process the divisor list corresponding to the middle number, use 2 pointers to keep the number of divisors from the divisor list corresponding to the smallest number (similarly for the largest) that are smaller than the current divisor from that middle list, then check all pairs of bitmasks (smallest, largest number) that are valid for that current divisor's bitmask and the current ordering; since we have the number of ways to choose the remaining two divisors, computing the answer is straightforward.
The advantage of this approach is that there's no need to think about what to add, what to subtract, which orderings to use etc. It's all just iterating over initially arbitrarily chosen things. The obvious disadvantage is that it's slow, I needed some optimisations in the last test (namely "if all pairs of bitmasks give 0, skip innermost loop").
Each A[i] gives a list of divisors divs[i][], which are the possible lengths of the i-th side of the parallelepiped. We want to take all triples (v[0], v[1], v[2]) such that v[i] appears in divs[i][], sort the numbers in each triple, and count how many of these sorted triples are distinct.
For each number, I check if it appears in divs[0][], in divs[1][], in divs[2][] and this gives a bitmask, e.g. divisor 72 has bitmask 110 if 72 appears in divs[0][] (divs[0][k]=72 for some k), appears in divs[1][] and doesn't appear in divs[2][].
Now instead of triples (v[0], v[1], v[2]) such that v[i] appears in divs[i][], I'll consider already sorted triples (w[0] <= w[1] <= w[2]) and add information of this kind: w[i] was from divs[id[i]][]. Basically, if we took a triple (v[0], v[1], v[2]), sorted it and got (w[0], w[1], w[2]), then id[] describes how it was sorted: v[id[0]] = w[0], v[id[1]] = w[1] and v[id[2]] = w[2].
Having both w[] and id[] completely defines the original triple v[], but we want to count just the number of different w[]-s (sorted triples).
Consider just a triple of bitmasks instead of triple of w-s: (bitmask(w[0]), bitmask(w[1]), bitmask(w[2])). Clearly two triples (w[0], w[1], w[2]) are different if their triples of bitmasks are different, so we just need to consider all triples of bitmasks and count the number of different triples (w[0], w[1], w[2]) for each of them.
Now let's say the current triple of bitmasks is (b[0], b[1], b[2]). What can the values of id[0], id[1], id[2] be? They obviously have to be all different. w[0] has to be a number from divs[id[0]][], so b[0] must have 1 on the id[0]-th position (as the id[0]-th bit) and similarly for all bitmasks, the id[i]-th bit of b[i] must be 1. E.g. if v[1] is the smallest out of (v[0], v[1], v[2]), then w[0] = v[1], id[0] = 1, so b[0] must be 010, 011, 110 or 111.
We need to assign id[] to each w[] with the current bitmask. Then each w[] corresponds to exactly one v[]. Of course, there's nothing saying how these id-s need to be assigned, so we can just generate all choices and choose one — any one. (It's possible that there are no valid choices for invalid triples of bitmasks. We can simply ignore these.)
Now that we've done it, we have some groups of numbers (b[0], b[1], b[2], id[0], id[1]); id[2] is uniquely determined from that since id-s need to form a permutation. Let's group them together by id[], not by b[], as we did until now. For a query, we can try all possibilities for id[], i.e. all permutations of divs[0][], divs[1][], divs[2][]; let's call them pd[0][] = divs[id[0]][] and similarly pd[1][] = divs[id[1]][]. We've got a list of bitmask-triples corresponding to this order. For each of these bitmask-triples (b[0], b[1], b[2]), we need to count the number of ways to choose w[0] in pd[0][], w[1] in pd[1][], w[2] in pd[2][] such that w[0] <= w[1] <= w[2], w[0] is a number with bitmask b[0] etc.
This is solvable with a standard 2 (actually 3) pointers algorithm: iterate over numbers in pd[1][] in increasing order (let's call the pointer to the number we're currently at "current_position"), keep a pointer to the last number in pd[0][] that's <= pd[1][current_position] and remember how many numbers before it had each bitmask (e.g. lt[011] numbers had bitmask 011), a similar pointer to the first number in pd[2][] that's >= pd[1][current_position] and remember how many numbers after it had each bitmask too (gt[b] numbers had bitmask b). When these pointers are moved, how many numbers had which bitmasks can be easily recomputed and this is still the fast part. For each "current_position", we should try all triples of bitmasks (b[0], b[1], b[2]) (precomputed before for these id[]-s) such that pd[1][current_position] has bitmask b[1]. The number of ways to take w[0] from pd[0][] with bitmask b[0] and w[2] from pd[2][] with bitmask b[2] to form a valid triple with pd[1][current_position] is lt[b[0]] * gt[b[2]]. Sum up these numbers. That sum is the final answer.
Sorry, it's incomprehensible. Can you give the code?
40362511
anybody got any implementation for Div1C second solution?!
Hello, I have a question about my algorithm on div 2D/ div 1B.
First, I made some observations (not sure if they are correct):
In order to divide the large parallelepiped into smaller (and equal) ones, we need each dimension of the small to be divisible by the corresponding dimension of the large.
By adhering to the above observation, we enumerate a lot of duplicate parallelepipeds. For example, the parallelepiped (2, 2, 2) can be split into the following ones:
(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)
but, in reality, we only need the (1, 1, 1), (1, 1, 2), (1, 2, 2) and (2, 2, 2).
So, I have thought that we can just create the dimensions in increasing order. That means if we have a tuple (a, b, c), we have the constraint: a <= b <= c.
Now, on the programming part:
For each query,
I find the divisors of a, b and c (the dimensions of the large parallelepiped).
I find the number of all the possible combinations of the divisors I found above such as if I have the (a, b, c) tuple, I accept only the ones where a <= b <= c. On this step, I do some optimizations in order not to trigger a TLE.
Here is my code for reference:
http://codeforces.com/contest/1008/submission/40527094
(it is a bit unorganized, but, on a top level I implement the above steps)
So, my question is what am I doing wrong?? It is difficult for me to make sense of the editorial and compare my solution to the ones provided in order to find my mistake!
Thanks in advance! Any help is highly appreciated!
your observations are correct. i think, what you are doing wrong is that you don't take into consideration that the orientation of the big parrallelepiped should not necessarily coincide with the orientation of the small parrallelepiped.
if the sides of the big parallelepiped are A, B and C, you are trying to find the solutions of the form a <= b <= c, where a | A, b | B, c | C. but you do not find the solutions of the form a <= b <= c, where a | B, b | C, c | A.
for example if the big parallelepiped is (3, 4, 5), you will not find the solution (2, 3, 5)
Thanks for the reply! I will try to solve the problem now! :)
Hi, can anyone please help me with my div2C submission, it is getting error on test case 8
Your idea is wrong
1007A — Reorder the Array — this problem can be solved by using two pointers . Here is my solution Link