Tutorial
Tutorial is loading...
Solution (Vovuh, O(n^2))
#include <bits/stdc++.h>
using namespace std;
#define sz(a) int((a).size())
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
string t;
cin >> n >> k >> t;
int cnt = 1;
int pos = 1;
string ans = t;
while (cnt < k) {
if (pos >= sz(ans)) {
ans += t;
++cnt;
} else {
bool ok = true;
int len = 0;
for (int i = 0; i < sz(t); ++i) {
if (pos + i >= sz(ans)) break;
++len;
if (ans[pos + i] != t[i]) ok = false;
}
if (ok) {
ans += t.substr(len);
++cnt;
}
}
++pos;
}
cout << ans << endl;
return 0;
}
Solution (Vovuh, prefix-function)
#include <bits/stdc++.h>
using namespace std;
#define sz(a) int((a).size())
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
string t;
cin >> n >> k >> t;
vector<int> p(n);
for (int i = 1; i < sz(t); ++i) {
int j = p[i - 1];
while (j > 0 && t[j] != t[i])
j = p[j - 1];
if (t[i] == t[j])
++j;
p[i] = j;
}
int len = sz(t) - p[n - 1];
for (int i = 0; i < k - 1; ++i)
cout << t.substr(0, len);
cout << t << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
#endif
int n;
scanf("%d", &n);
vector<int> a(n);
for (int i = 0; i < n; ++i)
scanf("%d", &a[i]);
int ans = 0;
for (int i = 0; i < n; ++i) {
int j = i;
while (j + 1 < n && a[j + 1] <= a[j] * 2)
++j;
ans = max(ans, j - i + 1);
i = j;
}
printf("%d\n", ans);
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 300 * 1000 + 13;
const int INF = int(1e9);
int n;
int prl[N], prr[N], sul[N], sur[N];
int l[N], r[N];
int main() {
scanf("%d", &n);
forn(i, n)
scanf("%d%d", &l[i], &r[i]);
prl[0] = sul[n] = 0;
prr[0] = sur[n] = INF;
forn(i, n){
prl[i + 1] = max(prl[i], l[i]);
prr[i + 1] = min(prr[i], r[i]);
}
for (int i = n - 1; i >= 0; --i){
sul[i] = max(sul[i + 1], l[i]);
sur[i] = min(sur[i + 1], r[i]);
}
int ans = 0;
forn(i, n)
ans = max(ans, min(prr[i], sur[i + 1]) - max(prl[i], sul[i + 1]));
printf("%d\n", ans);
return 0;
}
1029D - Concatenated Multiples
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
typedef long long li;
using namespace std;
const int N = 200 * 1000 + 13;
const int LOGN = 11;
int n, k;
int a[N];
int len[N];
vector<int> rems[LOGN];
int pw[LOGN];
int main() {
scanf("%d%d", &n, &k);
forn(i, n) scanf("%d", &a[i]);
pw[0] = 1;
forn(i, LOGN - 1)
pw[i + 1] = pw[i] * 10 % k;
forn(i, n){
int x = a[i];
while (x > 0){
++len[i];
x /= 10;
}
rems[len[i]].push_back(a[i] % k);
}
forn(i, LOGN)
sort(rems[i].begin(), rems[i].end());
li ans = 0;
forn(i, n){
for (int j = 1; j < LOGN; ++j){
int rem = (a[i] * li(pw[j])) % k;
int xrem = (k - rem) % k;
auto l = lower_bound(rems[j].begin(), rems[j].end(), xrem);
auto r = upper_bound(rems[j].begin(), rems[j].end(), xrem);
ans += (r - l);
if (len[i] == j && (rem + a[i] % k) % k == 0)
--ans;
}
}
printf("%lld\n", ans);
return 0;
}
1029E - Tree with Small Distances
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
const int N = 200 * 1000 + 11;
int p[N];
int d[N];
vector<int> g[N];
void dfs(int v, int pr = -1, int dst = 0) {
d[v] = dst;
p[v] = pr;
for (auto to : g[v]) {
if (to != pr) {
dfs(to, v, dst + 1);
}
}
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
#endif
int n;
scanf("%d", &n);
for (int i = 0; i < n - 1; ++i) {
int x, y;
scanf("%d %d", &x, &y);
--x, --y;
g[x].push_back(y);
g[y].push_back(x);
}
dfs(0);
set<pair<int, int>> st;
for (int i = 0; i < n; ++i) {
if (d[i] > 2) {
st.insert(make_pair(-d[i], i));
}
}
int ans = 0;
while (!st.empty()) {
int v = st.begin()->second;
v = p[v];
++ans;
auto it = st.find(make_pair(-d[v], v));
if (it != st.end()) {
st.erase(it);
}
for (auto to : g[v]) {
auto it = st.find(make_pair(-d[to], to));
if (it != st.end()) {
st.erase(it);
}
}
}
printf("%d\n", ans);
}
Tutorial
Tutorial is loading...
Solution (PikMike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
typedef long long li;
using namespace std;
const int N = 1000 * 1000;
int lens[N];
int k;
li solve(li a, li b){
k = 0;
for (li i = 1; i * i <= b; ++i)
if (b % i == 0)
lens[k++] = i;
li ans = 2 * (a + b) + 2;
li x = a + b;
int l = 0;
for (li i = 1; i * i <= x; ++i){
if (x % i == 0){
while (l + 1 < k && lens[l + 1] <= i)
++l;
if (b / lens[l] <= x / i)
ans = min(ans, (i + x / i) * 2);
}
}
return ans;
}
int main() {
li a, b;
scanf("%lld%lld", &a, &b);
printf("%lld\n", min(solve(a, b), solve(b, a)));
return 0;
}











May I know how to solve C using segment tree? A lot of folks seem to have done it this way.
You can use segment tree to get range min and range max instead of doing a clever precomp. This adds log factor. I did it with RMQ table because I am lazy.
You can use multiset to get O(n log n) with a simpler solution: 42096347
Brilliant!
Your solution looks really small and pretty. Can you explain the logic behind it ? I can't seem to get it.
Okay i got what you were trying to do. I guess multiset is actually a kind of Self-Balancing BST. Isn't it ? that's why we get n * log(n) solution.
Multiset works like a set, but allows repeated elements. We just need to find min R and max L, but each time ignoring one of the n intervals. We add all L's and R's to the multisets, and then, for each interval, remove it's values and check for max/min and get best value. It's easy to query because multiset is ordered like set, so min = .begin(), and max = .rbegin()
This can be used too in 2D like in this recent problem: 1028C - Rectangles
Solution with multisets: 42187139
My segment tree answers the question: What is the intersection segment of segments between index l and index r inclusive?
So, I just iterated over all i that 1 < = i < = n, and in each iterate I asked about the intersection segment of segments from 1 to i - 1 inclusive and the intersection segment of segments from i + 1 to n (i.e. I removed the segment with index i), then merged the two resulting intersection segment to obtain the segment which its length should enter in the result maximizing operation.
For merging two segments [a, b] and [c, d], the resulting segment is [lft, rht], where lft = max(a, c) and rht = min(b, d). Then if lft > rht let this segment equal to [ - 1, - 1] as a sign for the future merges that this segment contains nothing.
This is my submission.
I was actually looking at your solution before you replied! thanks!
How can we do this question using segment tree if we were allowed to remove (say) m segments at a time.
I really don't know, bro ;)
I used Sparse table for RMQ. Whenever I write sparse table, I feel very proud.
For problem B,
Can anyone tell me why is my solution failing?
http://codeforces.com/contest/1029/submission/42053121
Maybe you misunderstood the problem? for every index i, since the list is sorted, you just have to make sure i+1 is less than 2*a[i]. You only need one such value to satisfy the condition. Just replace your search function with a check 2*a[i]>=a[i+1] or something like that.
Here is one of my solutions for problem E which apparently works in linear time without dynamic programming.
It uses BFS
O(n+n-1) = O(n)to get vertexes sorted by distance from the first vertex.Your code has Python flavor.
What is this supposed to mean?
The problem E doesn't need any sorting, just dfs on a tree Code
The idea is to connect the parent of the furthest vertices to the first vertex, and then mark all parent's children as used ones.
Amazing solution :)
In D, can't you use a hashmap with the remainders mod k, instead of appending to rem_len_i and binary search? It should decrease the complexity to O(n) too.
do you mean D?
yes, you can. here is my (cleaned) solution (which is actually slower than PikMike's) ^_^
I meant D. Edited thanks! Thanks also for the solution leoniduvk!
I submitted D 15 times using an O(10 * n * 2) solution (i < j then i > j), finally passed systests with O(10 * n) by precomputing everything first then handling i != j
Your solution just has the same problem as the majority of all the others, you're doing
res += map[ x ]
without actually checking if x was in the map originally. This generates a lot of empty elements that add up to the complexity. Your submission got acccepted with 1980 ms, submit the same code again and it might not even actually get accepted.
Still TLEs even with the find check
I know you have checked; what i am saying is that your program still uses a lot of memory, like when i wasn't doing the check, so there's gotta be something wrong.
So you could run some tests displaying the size of the map(s) before and after inserting some known amount of elements, and checking whether that's correct or not.
can someone help me i am getting tle for 1029D — Concatenated Multiples https://onlinegdb.com/rks1jEywm
Check this condition ,or else element temp will be created and inserted in map. And changed long long to unsigned long long
link
thanks!, It works for me, i didnt know that a[i]=0 that element is inserted in map
thank you! it worrked
My solution for F is getting WA for test case #37 42102854. Can someone please take a quick look? Edit: nevermind, found a silly mistake.
val can be more than INT_MAX, use long long everywhere
thank you!
On problem E i got WA on testcase 11. The answear differs by 1. Can anyone tell why? Code : http://codeforces.com/contest/1029/submission/42104188 Edit: Fixed.
The following is a simple and compact C++17 solution for problem 1029A - Many Equal Substrings using the STL function
string::substr().42106199
Thanks.**Very Clean Code**!!
I solved E using dynamic programming in linear time but it is failing test case 8 , Can someone tell me what is wrong with my code ?
The answer to this test should be 2. 1 -> 5, 1 -> 8.
Got it! Thanks for the help! :)
I can't understand why my solution of problem C fails. Can anyone help me?
Check this test case:
Thanks! I've just found the error... It was a such stupid one
Can someone explain DP on tree solution for Problem E?
If you are trying to solve E with DP and are having some WA submissions then I suggest try these following 2 test cases. It is just my humble advice but I did use those 2 cases to find out the AC method.
test 1 (answer is 2: you need (1 -> 5) and (1 -> 8) (thanks a guy up there for this test :D)):
test 2 (answer is 2):
First of all, you can see that we have already had a tree with the root is vertex 1. Since the shortest path from vertex 1 to any other vertex at most 2, you may come up with this idea: let f[u][i] be the minimal number of edges that should be added so that the shortest path from 1 to u is i and the subtree with root vertex is u satisfy the given condition. Thus, every vertex has 2 states: f[u][1] and f[u][2]. However, later you will see that every vertex has 3 states :v
If the distance from vertex 1 to u is 1, it can easily be seen that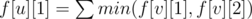 (v is a child vertex of u).
(v is a child vertex of u).
If the distance from vertex 1 to vertex u is 2, vertex u is sure to be connected with a vertex that has the shortest path from vertex 1 is 1. Here now there are 2 options: connect u with its direct ancestor or a child vertex of it. In order to implement, I denote the second subcase as f[u][3].
f[u][3] = min(f[u][2] - min(f[v][1], f[v][3]) + f[v][1])
In addition, it can be seen that the base cases are those leaves of the tree and f[u][1] = 1, f[u][2] = 0, f[u][3] = ∞.
Look through my AC code ?
Sorry if you consider my English is bad :(
thank you for such a detailed and understandable explanation)
Can someone give better explanation for problem D?
For D, we can maintain an array tenp for (10i)modk, for 1 ≤ i ≤ 10 (since maximum number of digits is 10). We can also maintain a
HashMap, that maps the modulus to it's count. That is the key is (A[i])modK,and the value is the number of times a number in A, that has the same value after moding by k.Now, for every number A[i], we have to find numbers b such that (b × 10d + A[i])%k = 0.(Where d is the number of digits in A[i]). This can be written as,
. Let $1$ n = A[i]%k , α = (10d)%k and m = b%k. So, it becomes:
Thus, if $n=0$, then, we can satisfy the condition when m = 0 or when α = 0. We can search for the number of times a zero is inside the
HashMap, for checking the m = 0 condition. If α = 0, then we know that every number int A can be used to satisfy the condition, as the whole number will always be divisible by k.Now, if n > 0, then (m × α)%k = (k - n), thus,
Thus, we'll just have to count the number of occurrences of $m$ inside the
HashMap.My implementation didn't work quite well, so I think there must be some quirk left behind that may make this implementation unreasonable. Any help appreciated!
Can someone help me with 1029D.http://codeforces.com/contest/1029/submission/42209023
For the explanation of question F, what do they mean by "a+b should be area of the outer rectangle." Like is there even an outer rectangle?
In problem D, the only difference between the editorial and my approach is that i've used "unordered_map<int,int> mp[11]" where mp[d][x] stores the frequency of numbers which have d digits and leave a remainder x when divided by k. I get TLE. why?
This is the link to my solution. 42241992
I used an ordinary map, and I too faced the same issue.
Apparently, checking if an element is present in the map before trying to retrieve it, significantly reduces the running time.
In your code, instead of
do a
Helped alot!! Thanks bro.
For problem A, isn't the first idea in O(n^3)? Because for this example 'aa..aac', for every k we need to verify the prefix in (n * (n + 1)) / 2 steps. But in the first solution, which implements this idea, the author says that it's in O(n^2) 'Solution (Vovuh, O(n^2))'.
In problem 1029C — Maximal Intersection .
Intersection of some segments [l1,r1],[l2,r2],[l3,r3],....,[ln,rn] is [max li,min li].If this segment has its left bound greater than its right bound then the intersection is empty.Can anyone give me proof of this. I want to know why this happens?
We want to find the longest segment that is an intersection of some segments [l1,r1], [l2,r2], ..., [ln,rn]. To maximize the length, we want to find the leftmost and rightmost points on this segment.
The leftmost point guaranteed to be in all the segments is max(li) for some i. To prove this, we can use contradiction. Assume the leftmost point guaranteed to be in all segments is lj, for some lj < li and j != i. But then the i-th segment (with endpoints [li, ri]) is not guaranteed to be in the wanted intersection, because a case like rj < li is possible (you can visualize the segments as: [lj]----[rj]....[li]--------[ri]). Therefore the assumption is false and the original claim is true.
Similar logic for the rightmost point.
In Problem C, instead of storing result in partial sum like arrays, we can store 4 values which are max of left, min of right and second largest max of l, second largest min of r.
Now, my result is min — max > 0 ? min — max : 0.
So, now I iterate over all the segments and see if removing that improves my answer which maximum length intersection between the remaining.
if the current segments left is equal to max then I replace max my second largest max, else it remains same. Similarly, if current segments right is equal to min then I replace min by second largest min, else it remains same.
Now I keep checking in the loop if my result increases and finally output the maximum result.
This solution also works in O(n) but extra space complexity is reduced to O(1), since it does not require partial sum array.
43075255
Can you please explain why this logic works?
Hi,
For any given set of line segments,
intersection length = max(left indices) - min(right indices).And for an intersection to occur, this number must be greater than 0.
Now, if I have to remove 1 segment so as to increase the intersection length, I have to keep track of the new max and min after removing that segment.
So, basically I will loop over all segments and calculate new intersection length after removing that segment.
For, instance if I remove a segment whose left index was max, then I have to resort to second max in order to calculate the new intersection length, because that is the new left max now.
Similarly for min right and second min right.
Therefore, I have to keep track of max of left, second max of left and min of right, second min of right.
Since I am removing only 1 segment therefore storing these 4 value will work, whereas if I had to remove k segments then I would have to store more values.
Therefore, this logic will only work for this particular problem statement only.
How to solve this for removing k segments?
Above, logic won't work for removing k segments, and removing k segments is indeed a very good question.
Naive Solution: Brute Force using recursion. Complexity O(n^k).
Better Solution: I will get back to you on this.
how can it be done within O(n) complexity?
By using greedy approach, I think it can be done in O(n*k), but I can't think of any solution in O(n). In fact, I don't think there is any solution in O(n).
how? I mean how can we get all possible subsets in O(n*k). As for removing k segments we have to pick k segments out of n total segments. Any pseudocode will be helpful.
In greedy approch we reduce a problem into a smaller problem, using a safe move. So, if the safe move is right then the algorithm will work. For this case, for an array of n elements, just remove 1 segment which will maximise the intersection. This will reduxe it to a problem of sizs n-1. Now, we will remove a single segment from array of size n-1 to maximise intersection thereby reducing it to an array of size n-2. Then just continue till the array is reduced to size n-k.
Here each reduction will take O(n) since in each reduction we are removing 1 element. Therefore, O(n*k).
Also this is based on the assumption that the safe move is correct. If you’ve the test cases I think it’s worth a try. I think it will work.
But I guess that all possible subsets of size k should be removed once and then the maximum intersection possible should be checked. Similarly for other possible subsets of array with size k should be removed and score should be calculated. Shouldn't this be correct ?
You're not getting the point. Okay, let's try to understand using another problem.
Let's say you've to find k minimum elements in array.
Would you extract every possible subset of size k and see if these are k minimum elements.
Or would you find the minimum element and then the second minimum element, and so on, until you reach k minimum elements.
This is known as greedy approach, where I am reducing the problem size by finding minimum element to n-1, and then finding the minimum element in new reduced array of size n-1.
Now, do you get the point ? Yes, you can find the answer, by finding all possible subsets, but that's not very efficient. It's like saying you can sort an array in O(n^2). Yes you can, but you do have more efficient and complex algorithms for the same.
Now, coming back to the original problem, I understand that greedy approach might be a little difficult to digest.
But try to generalize the problem by removing 1 segment, then 2 segments, 3 segments and so on. You will see a pattern.
And if you still don't, try to read more about greedy algorithms, and simple problems which can be solved by using greedy algorithms, this will seem very easy then.
can anyone explain me how to solve problem A ? i can't understand the tutorial :|
I think the time limit of D is too strict.
The key idea in problem E is that: The set represents the vertices which are not yet reachable from 1 in at most 2 steps. Then greedy algorithm for the farthest vertex suffices.
in "CREATING CONTEST" what will be the output if i/p is 1 4 5 7 9 10
$$$4$$$, since we can use problems with difficulties $$$5$$$, $$$7$$$, $$$9$$$, $$$10$$$.
D was a great problem for performance freaks