Roms's blog

Codeforces Round #509 (Div. 2) Editorial
By Roms, history, 6 years ago, In English

1041A - Heist

Tutorial
Solution

1041B - Buying a TV Set

Tutorial
Solution

1041C - Coffee Break

Tutorial
Solution

1041D - Glider

Tutorial
Solution

1041E - Tree Reconstruction

Tutorial
Solution

1041F - Ray in the tube

Tutorial
Solution
  • Vote: I like it
  • +148
  • Vote: I do not like it

Comments Comments (82)
| Write comment?
»
6 years ago, # |
  Vote: I like it +73 Vote: I do not like it

quickest editorial posted ever! well done!

→ Reply
»
6 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Thank you for giving editorials that fast ...contest was really good ..hope this will continue in future

→ Reply
»
6 years ago, # |
  Vote: I like it +14 Vote: I do not like it

The hack test of "1041F Ray in the tube" is: 1 0 1 1 0 1

The right answer is 2, but you may print 1.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    Shouldn't y1 be smaller than y2?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Take this case
      1 1
      1
      1 2
      1
      The main corner case is including points with same x coordinate on the same ray

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +4 Vote: I do not like it

thanks Roms for the editoriel

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

Kudos to the organizers for posting the editorial so quickly

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

thanks you :>

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

The tutorial of C seems like a greedy algorithm. I'm wondering how to prove it and need help. During the contest, I'm unsure and I wrote a binary search algorithm with complexity of O(n(logn)^2).

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    I'm not sure, but maybe it goes something like this. Let a be the element you've just picked. Now, for any element greater than a+k, the smallest(a1) is the optimum via greedy. Let's assume it's not and let a2 be the element we pick. Now, the sequence of elements which you pick after a2 will also be valid if you had picked a1 initially. However, picking a1 might have let you take more elements which you might not have been able to take had you picked a2, which potentially reduces the number of days and thus may give a better answer.

    What's your binary search solution?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      Thanks, but there're some confusions. When considering using more coffee breaks in one day, choosing a1 is of course better than a2 because we have more potential elements. But how can this way make the number of days least?

      As for my own solution, I guess an answer in range of [1,n] and make checks. When checking I used priority_queue to remember the best choice among these days. While picking a new element, if difference of the element and the top of the queue is not more than d, the answer is too small.

      This is my code-> http://codeforces.com/contest/1041/submission/42932521

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, I am silly to use priority_queue… It's easier to memorize the best choice… Maybe my solution is same as Adibov's.

        → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I don't think greedy works for C. The following input:

    4 10 3
1 5 6 9

    is possible in two days (1 6 on first day, 5 9 on second day). Greedy will give 1 5 on first day, 6 on second day, 9 on third day. Unless I misunderstood something, which is not improbable :-)

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Greedy will give 1,5,9 on the first day and 6 on the second day. So while your partition works, so does the greedy solution's.

      → Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

great work ! fast editorials do help!

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks guys for the quick editorial post!

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In F, I don't understand why choose dx is power of 2, not power of 3 or power of 100? And how to prove that choose power of 2 is optimal?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    If you choose dx as power of 3 or 4 or 100, you will find some situations cannot be represented. Assume d=m*dx^l, sometimes using dx cannot hit all points using d.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I think we can always represent in base 3, example: 5 = 5 * 3^0. Hmm, maybe I need a prove why we choose power of 2

      → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +27 Vote: I do not like it

    Suppose that the ray is emitted from the point Ax, and d is a positive number that can be divided by some prime p such that p ≠ 2. Then if we choose dx = d, we will visit Ax + d, Ax + 3d, Ax + 5d... on the opposite side of the tube and Ax, Ax + 2d, Ax + 4d... on the same side of the tube where we started the ray.

    Then let's choose . On the opposite side of the tube, the ray will pass through 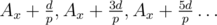, and since p is odd, then Ax + d, Ax + 3d, Ax + 5d... is a subsequence of this sequence! The same applies for the positions we visit on ''our'' side of the tube.

    So, if dx is divisible by some odd prime p, then dividing it by p doesn't make the answer less, and we can eliminate all odd prime divisors of dx one-by-one.

    → Reply
»
6 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Why the problem E's constraints too small. It just confusing.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    It's confusing for me too. E's complexity is a mere O(N), which should have gotten N <= 10 ^ 5 or something. I even thought my algorithm was wrong (didn't have any proof of correctness), but the tutorial did exactly what I did.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +54 Vote: I do not like it

    In fact, my solution for this problem (which is in the editorial) is , but I've decided to give n ≤ 1000 for one reason: as for me, the core of this problem is the idea how we check if the tree can be reconstructed and how we actually reconstruct it. Changing the constraints to n ≤ 2·105 doesn't add anything to the idea of the problem. Yes, it changes the implementation, but I personally don't like to enforce some implementation-wise constraints on problems with constructive algorithms, if they don't enforce a solution with completely different idea.

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Perhaps it's also because it's more convenient to implement an O(n2) algorithm than an O(n) one when checking whether an answer is valid.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Well I mean for people like me who was only able to come up with an O(n) solution we look at the limit and will start thinking that our algorithm is wrong, while in fact, it is correct. And I feel the O(n) solution's implementation is pretty simple, I did about 50 lines of code only.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Same...

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Actually I mean it's harder for problem setters to implement the checker in O(n) time than in O(n2).

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +3 Vote: I do not like it

          Lol nah, for O(n) you just gotta use an array f[i] and get maximum from all its children. For O(n ^ 2) you gotta re — dfs into the subtree which is lotta work.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            Emm you are right. I forgot we can fix the maximum to be the root and calculating 1 maximum value instead of 2. My original thoughts were too complicated.

            → Reply
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Can anyone help me figure out why my solution is giving me TLE verdict. My approach is similar to that of editorial. Link to my solution http://codeforces.com/contest/1041/submission/42951879

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +2 Vote: I do not like it

    You got the same problem as I, the lower_bound from standard "algorithm" library won't run in O(logN) time complexity with the set data structure (I guess it is O(n)?), so you should use the one from "set" library which is s.lower_bound(...);

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +6 Vote: I do not like it

Today I learned that using regular lower/upper_bound from "algorithm" library on a set is not as same as the one from "set" library, which took me a TLE in problem C.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Lol lower_bound upper_bound in the standard library can't access set elements directly as opposed to the set library's lower_bound. So their access takes actually O(n), which is pretty expensive.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Yeah but while i was coding i didn't know that :(. But why it is not an error when you call that kind of function on a set?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        Well because it's still a valid call. The compiler isn't responsible for your poor life choices :)

        → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Me, too. I think they should fix this problem. If the compiler smarter it will use set::lower_bound automatically.

    → Reply
»
6 years ago, # |
  Vote: I like it +12 Vote: I do not like it

I have a different approach for problem F, and also a different proof for the distance "2l" in the tutorial.

Let A and B be the set of points from the first and second lines respectively. Let's split A into 2 sets, Aodd — the set that contains odd points — and Aeven — the set that contains even points. Do the same for B.

So here are some observations:

  • The ray cannot reach both points from Aodd and Aeven, or both points from Bodd and Beven.
  • Two of possible solutions are: combine Aodd and Beven, or combine Aeven with Bodd. The distance dx for these solutions is 1.

From here we have 2 subproblems that are very similar to the initial problem:

  • The first line contains points from Aeven and the second one contains points from Beven.
  • The first line contains points from Aodd and the second one contains points from Bodd.

We can solve these 2 recursively. Let's deal with the first one. We can safely, divide all the number from Aeven and Beven by 2. By doing so, we are now turned back to the initial problem, with new A is new Aeven and new B is new Beven. With the odd ones, first we subtract all the numbers by 1, and then divide them by 2. So, the problem is solved.

We can see that after dividing step, the distance between numbers is also divided by 2. That way, if we keep taking dx = 1, we are actually taking dx = 2, 22, ..., 2l where l is the recursion's level.

I implemented the solution with recursion, but I got MLE. So I do some tricks and optimized it with Trie. Sadly, I fail at test 79, where the first and second line contains the same number. :(

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +11 Vote: I do not like it

    Cool solution!!!

    I tried your approach and it worked even without optimizing memory. I think the issue in your case might have been less base-cases in the recursion.

    Without memory optimization: 43012783

    With memory optimization: 43012648

    For memory optimization, I just free the arrays/vectors as soon as there is no further use of them.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Nice implementation!

      I think you are absolutely right, I was bad at handling cases. Your implementation is very clean! And thank you for reading my comment! I thought I was alone here :)

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Now I know std::set::lower_bound is much more faster than std::lower_bound(set).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    the problem is NOT lower bound! the problem is erasing the first element of a vector! deleting the first value in a vector is in O(n) since all values need to be moved by one position your first solution is therefore in O(n^2)

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I use set, not vector.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 5   Vote: I like it 0 Vote: I do not like it

        https://codeforces.com/contest/1041/submission/42956788 line 17: vector<pair<int, int>> A; line 25: A.erase(A.begin());

        the std::lower_bound function on a vector is normally much faster than set.lower_bound... (and if you use std::lower_bound on a set its time complexity is also O(n^2) since a set has no random access)

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I submit that question over 20 times. https://codeforces.com/contest/1041/submission/42934245 And this is one of those, which using set and std::low. And also this is in the contest, while 42956788 is not.

          Initially, I use vector and get TLE on pretest 10. But when I change vector to set, it become TLE on pretest 9! So I keep using vector after that.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
            ← Rev. 3   Vote: I like it 0 Vote: I do not like it

            as i said in that submission you use std::lower_bound on a set. a set has NO random access! even the documentation tells you that the complexity of this is O(n^2)

            but still std::lower_bound on a data structure with random access is much quicker than the set!

            so in other words: you did not get TLE because std::lower_bound is to slow but because you used it on a data structure which does not fit the requirements!

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Yes, what I mean is what you said. And I have fixed the first comment.

              → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      if you want to delete first element from vector<int>, you can use deque<int> instead.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        yeah but he is not only deleting the first element ^^

        → Reply
»
6 years ago, # |
  Vote: I like it +13 Vote: I do not like it

I have another solution for problem C: after sorting array consider the largest block that first element and last element of the block can't be in one day. We claim that answer is size of that block and if block start from L to R, we start writing 1 to R-L+1 from L to R and continue from each side. for example if n = 8 and L = 3 and R = 6, we make new array like this:

3 4 1 2 3 4 1 2

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is it everyone constructed a path in problem E? It came to my mind, but I was all tried to find counter-case. I wasn't sure. Towards the end, I tried to construct the answer from the initial case which was star with vertex n in the center. Then appending path's to one another. Leaving all vertices i such that cnti = 1 as leaves. Didn't complete though.

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I tried problem D using sliding window technique, the glider can jump from left of any block or till the right of any block, but got wrong answer on test 11. Please anyone can look into my code and point out the mistake. https://codeforces.com/contest/1041/submission/42958431

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can someone please explain the runtime difference between this and this code? The only difference between them is that in one pair is of data type <long long, long long> and in other it's <int, int>.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    problem is not due to long long but because you didn't include if(cur > m) cur = 1, ans++; in your TLE'd code. I submiited your code after including that and got AC.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain D. I'm not getting it. If sorting is done, the order of airflows change. Also shouldn't more priority be given for longest airflows?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You don't sort in problem D, instead take prefix sums which is increasing, so already sorted. Then do lowerbound on that prefix sum.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The problem E has a O(n) solution.Why the limit is n<=1000?Does this problem has a solution with O(n^2)?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone tell why i am getting runtime error: http://codeforces.com/contest/1041/submission/42953329

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You are getting a TLE, not a runtime error. It is because std::lower_bound has complexity O(N) for containers that do not have random-access iterators. However, std::set::lower_bound has O(log(N)) complexity, which you can use. You can read more about them here and here.

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

How exactly can we do Problem D using two pointers ?

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    The first pointer is the place we choose to start flying,and the second pointer is the place we will reach the ground.It is obvious that it's better for us to start flying at the start of an ascending air flows.

    Oh my English is so poor!

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But we don't know where we will reach on the ground. Do we ?

      So, how do we place the second pointer ? How to scan to get the job done ?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        To be honest,I don't know how to tell you in English...

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it 
        #include<cstdio>
#include<algorithm>
#include<cstring>
#define ll long long
using namespace std;
ll n,h,from[200005],to[200005],sum[200005],down[200005],ans;
int main()
{
	scanf("%I64d%I64d",&n,&h);
	for(int i=1;i<=n;i++)
	  scanf("%I64d%I64d",&from[i],&to[i]);
	if(n==0)
	{
		printf("%I64d\n",h);
		return 0;
	}
	for(int i=1;i<=n;i++)
	  sum[i]=sum[i-1]+to[i]-from[i];
	for(int i=1;i<n;i++)
	  down[i]=down[i-1]+from[i+1]-to[i];
	down[n]=2147483647;
	int now=1;
	for(int i=0;i<n;i++)//i is the first pointer
	{
		while(down[now]-down[i]<h)now++;//now is the second pointer
		ans=max(ans,sum[now]-sum[i]+h);
	}
	printf("%I64d\n",ans);
	return 0;
}
        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem F I found test 51 has n = 12000 and m = 32000 and the answer is 24000, I thought the answer is at least 32000

I can choose the laser start at a side of the tube, and let it go straight.

The problem didn't said line AB cannot parallel with the side of tube.

Also , I may choose B out of tube

For example, if y1=0 and y2=1 I choose A(1,0) and B(2,2) and It would reflect at point (1.5,1) then return to (2,0)

In this way I can also get all the point with one single line.

My submission 43065546

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problm D, why answer to test 5 10 3 4 10 11 12 13 14 16 18 20 is 16? If he starts his flight at (3,10) th answer is 17.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If he will start at (3,10) then at X=18 H will be equal to 0, and he can't fly with H=0.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Quick Solution of Problem D using two pointers 43088242

→ Reply
»
6 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

can anyone help me identify what is wrong with my algorithm and what are the cases that i am missing

prob : 1041C — Coffee Break

https://codeforces.com/contest/1041/submission/43109819

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

At problem D, why is the complexity o(n*log(n)*log(10^9))? Isn't it essentially binary searching 10^9 numbers for every n? Shouldn't it just be n*log(10^9)?

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please help what's issue with this submission, failing in case 9 Your text to link here...

→ Reply