Tutorial
Tutorial is loading...
Solution
#include <set>
#include <algorithm>
#include <iostream>
#include <vector>
#include <string>
#include <cassert>
using namespace std;
const int N = 100 + 13;
int n, m;
int a[N];
int main() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
int ans2 = *max_element(a, a + n) + m;
for (int it = 0; it < m; it++) {
int pos = -1;
for (int i = 0; i < n; i++) {
if (pos == -1 || a[i] < a[pos]) {
pos = i;
}
}
assert(pos != -1);
a[pos]++;
}
int ans1 = *max_element(a, a + n);
cout << ans1 << ' ' << ans2 << endl;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9;
int n;
map<string, int> was;
inline void read() {
cin >> n;
for (int i = 0; i < n; i++) {
int c;
string s;
cin >> c >> s;
sort(s.begin(), s.end());
if (was.count(s) == 0) {
was[s] = c;
} else {
was[s] = min(was[s], c);
}
}
}
inline int getC(string a, string b) {
if (!was.count(a) || !was.count(b)) {
return INF;
}
return was[a] + was[b];
}
inline void solve() {
int ans = INF;
if (was.count("A") && was.count("B") && was.count("C")) {
ans = was["A"] + was["B"] + was["C"];
}
if (was.count("ABC")) {
ans = min(ans, was["ABC"]);
}
ans = min(ans, getC("AB", "C"));
ans = min(ans, getC("A", "BC"));
ans = min(ans, getC("AC", "B"));
ans = min(ans, getC("AB", "BC"));
ans = min(ans, getC("AC", "BC"));
ans = min(ans, getC("AC", "AB"));
if (ans == INF) {
ans = -1;
}
cout << ans << endl;
}
int main () {
read();
solve();
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
scanf("%d", &n);
vector<int> a(n);
for (int i = 0; i < n; ++i)
scanf("%d", &a[i]);
int cntneg = 0;
int cntzero = 0;
vector<int> used(n);
int pos = -1;
for (int i = 0; i < n; ++i) {
if (a[i] == 0) {
used[i] = 1;
++cntzero;
}
if (a[i] < 0) {
++cntneg;
if (pos == -1 || abs(a[pos]) > abs(a[i]))
pos = i;
}
}
if (cntneg & 1)
used[pos] = 1;
if (cntzero == n || (cntzero == n - 1 && cntneg == 1)) {
for (int i = 0; i < n - 1; ++i)
printf("1 %d %d\n", i + 1, i + 2);
return 0;
}
int lst = -1;
for (int i = 0; i < n; ++i) {
if (used[i]) {
if (lst != -1) printf("1 %d %d\n", lst + 1, i + 1);
lst = i;
}
}
if (lst != -1) printf("2 %d\n", lst + 1);
lst = -1;
for (int i = 0; i < n; ++i) {
if (!used[i]) {
if (lst != -1) printf("1 %d %d\n", lst + 1, i + 1);
lst = i;
}
}
return 0;
}
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 200 * 1000 + 13;
int n;
long long T;
int a[N];
int f[N];
void upd(int x){
for (int i = x; i < N; i |= i + 1)
++f[i];
}
int get(int x){
int res = 0;
for (int i = x; i >= 0; i = (i & (i + 1)) - 1)
res += f[i];
return res;
}
int main() {
scanf("%d%lld", &n, &T);
forn(i, n)
scanf("%d", &a[i]);
vector<long long> sums(1, 0ll);
long long pr = 0;
forn(i, n){
pr += a[i];
sums.push_back(pr);
}
sort(sums.begin(), sums.end());
sums.resize(unique(sums.begin(), sums.end()) - sums.begin());
long long ans = 0;
pr = 0;
upd(lower_bound(sums.begin(), sums.end(), 0ll) - sums.begin());
forn(i, n){
pr += a[i];
int npos = upper_bound(sums.begin(), sums.end(), pr - T) - sums.begin();
ans += (i + 1 - get(npos - 1));
int k = lower_bound(sums.begin(), sums.end(), pr) - sums.begin();
upd(k);
}
printf("%lld\n", ans);
return 0;
}
1042E - Vasya and Magic Matrix
Tutorial
Tutorial is loading...
Solution
#include<bits/stdc++.h>
using namespace std;
const int MOD = 998244353;
const int N = 1009;
int mul(int a, int b){
return int(a * 1LL * b % MOD);
}
void upd(int &a, int b){
a += b;
while(a >= MOD) a -= MOD;
while(a < 0) a += MOD;
}
int bp(int a, int n){
int res = 1;
for(; n > 0; n >>= 1){
if(n & 1) res = mul(res, a);
a = mul(a, a);
}
return res;
}
int inv(int a){
int ia = bp(a, MOD - 2);
assert(mul(a, ia) == 1);
return ia;
}
int n, m;
int a[N][N];
int dp[N][N];
int si, sj;
int main() {
//freopen("input.txt", "r", stdin);
scanf("%d %d", &n, &m);
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
scanf("%d", &a[i][j]);
scanf("%d %d", &si, &sj);
--si, --sj;
vector <pair<int, pair<int, int> > > v;
for(int i = 0; i < n; ++i)
for(int j = 0; j < m; ++j)
v.push_back(make_pair(a[i][j], make_pair(i, j)));
sort(v.begin(), v.end());
int l = 0;
int sumDP = 0, sumX = 0, sumY = 0, sumX2 = 0, sumY2 = 0;
while(l < int(v.size())){
int r = l;
while(r < int(v.size()) && v[r].first == v[l].first) ++r;
int il = -1;
if(l != 0) il = inv(l);
for(int i = l; i < r; ++i){
int x = v[i].second.first, y = v[i].second.second;
if(il == -1){
dp[x][y] = 0;
continue;
}
upd(dp[x][y], mul(sumDP, il));
upd(dp[x][y], mul(x, x));
upd(dp[x][y], mul(y, y));
upd(dp[x][y], mul(sumX2, il));
upd(dp[x][y], mul(sumY2, il));
upd(dp[x][y], mul(mul(-x - x, sumX), il));
upd(dp[x][y], mul(mul(-y - y, sumY), il));
}
for(int i = l; i < r; ++i){
int x = v[i].second.first, y = v[i].second.second;
upd(sumDP, dp[x][y]);
upd(sumX2, mul(x, x));
upd(sumY2, mul(y, y));
upd(sumX, x);
upd(sumY, y);
}
l = r;
}
printf("%d\n", dp[si][sj]);
return 0;
}
Tutorial
Tutorial is loading...
Solution (O(n log n))
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < int(n); ++i)
#define sz(a) int((a).size())
const int N = 1000 * 1000 + 13;
int n, k;
vector<int> g[N];
int ans;
int dfs(int v, int p = -1){
if (g[v].size() == 1)
return 0;
vector<int> cur;
for (auto u : g[v]){
if (u == p) continue;
cur.push_back(dfs(u, v) + 1);
}
sort(cur.begin(), cur.end());
while (sz(cur) >= 2){
if (cur.back() + cur[sz(cur) - 2] <= k)
break;
++ans;
cur.pop_back();
}
return cur.back();
}
int main(){
scanf("%d%d", &n, &k);
forn(i, n - 1){
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
g[v].push_back(u);
g[u].push_back(v);
}
forn(i, n){
if (sz(g[i]) > 1){
dfs(i);
break;
}
}
printf("%d\n", ans + 1);
return 0;
}
Solution (Small to Large, O(n log^2 n))
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < int(n); ++i)
#define sz(a) int((a).size())
const int N = 1000 * 1000 + 13;
int n, k;
vector<int> g[N];
multiset<int> val[N];
int ans;
void dfs(int v, int d, int p){
if (g[v].size() == 1){
val[v].insert(d);
return;
}
int bst = -1;
for (auto u : g[v]){
if (u == p) continue;
dfs(u, d + 1, v);
if (bst == -1 || sz(val[u]) > sz(val[bst]))
bst = u;
}
swap(val[bst], val[v]);
for (auto u : g[v]){
if (u == p || u == bst) continue;
for (auto it : val[u]){
int dd = k + 2 * d - it;
auto jt = val[v].upper_bound(dd);
if (jt == val[v].begin()){
val[v].insert(it);
}
else{
--jt;
int t = *jt;
val[v].erase(jt);
val[v].insert(max(it, t));
}
}
}
}
int main(){
scanf("%d%d", &n, &k);
forn(i, n - 1){
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
g[v].push_back(u);
g[u].push_back(v);
}
forn(i, n){
if (sz(g[i]) > 1){
dfs(i, 0, -1);
printf("%d\n", sz(val[i]));
break;
}
}
return 0;
}
Solution (O(n))
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < int(n); ++i)
#define sz(a) int((a).size())
const int N = 1000 * 1000 + 13;
int n, k;
vector<int> g[N];
int ans;
int dfs(int v, int p = -1){
if (g[v].size() == 1)
return 0;
vector<int> cur;
for (auto u : g[v]){
if (u == p) continue;
cur.push_back(dfs(u, v) + 1);
}
int pos = -1;
forn(i, sz(cur)) {
if (cur[i] * 2 <= k && (pos == -1 || cur[pos] < cur[i]))
pos = i;
}
if (pos == -1) {
ans += sz(cur) - 1;
return *min_element(cur.begin(), cur.end());
}
int res = -1;
forn(i, sz(cur)) {
if (cur[pos] >= cur[i]) continue;
if (cur[i] + cur[pos] <= k && (res == -1 || cur[i] < cur[res]))
res = i;
}
forn(i, sz(cur))
ans += (cur[i] > cur[pos]);
if (res != -1)
--ans;
return (res == -1 ? cur[pos] : cur[res]);
}
int main(){
scanf("%d%d", &n, &k);
forn(i, n - 1) {
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
g[v].push_back(u);
g[u].push_back(v);
}
forn(i, n) {
if (sz(g[i]) > 1) {
dfs(i);
break;
}
}
printf("%d\n", ans + 1);
return 0;
}











so fast :/
So not available :/
now it is ;)
gone in a flash :o
Wow, I failed C because of writing >= 2 instead of >= 1
Loving the quick editorials !
F*cking Monikaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa........
Back to Back contest. And Back to Back fast editorial. I'm loving it.
I'm loving quick editorials. Really helpful.
Hey can you please explain the line "It's easy to see that the answer for the fixed L is n∑R=Lpref[R]<t+pref[L−1]. We can calculate this formula using some data structure which allows us to get the number of elements less than given and set the value at some position. "?
I didn't understand that Question's Editorial much.(Mostly because i have little experience with BIT and Segment trees).
I did that question D after the contest using a modification of the merge sort(I read that in a comment somewhere). You can read this comment It might be helpful.
But overall you need to learn BIT or Segment tree to make sense of the editorial at all.
Thanks a lot :) . In that comment the algorithm used is BIT right? and not merge sort?
For F,(untested)
I was thinking of fixing the centers of subtree formed by the leaves. For fixing centers, we greedily move from lowest to highest depth(from bottom to top) and pick centers when necessary. Also to avoid problems, we can assume k is even (If not add some dummy vertices and make it even).Now from a center we want distance to farthest not yet taken leaf node to be k/2 (which is what I mean by when necessary).
Does this work?
i think it works but it's hard to code(for me)
Got TLE on tc 68 in C, DAAH! :(((((((((((((((( .
.
.
.
.
.
.
Because of cin,cout DOuble DAAH! :(((((((((((((((((((
I feel u bro....
damn fastIO
I never use cin
Can anyone explain me solution to Problem D?
Let's say the input is A[1...n]. You first take the cumulative sum of A. Let this sum is S[1...N].
So by the property of S, you know that the summation of any subarray from j + 1 to i is S[i] - S[j], right?
Now, for each i, you want to find out how many j < i are there such that S[i] - S[j] < t. We rewrite the above as S[i] - t < S[j] i.e S[j] > S[i] - t.
So, for each i, you take S[i] - t and find number of previous values S[j] where j < i. This can be done in Segment Tree or Fenwick Tree by doing coordinate compression, or simply you can use C++11 Order Statistics Tree from gnu pbds.
Thanks!
How to apply coordinate compression in segment tree in this problem? I wrote a solution with only segment tree and got TLE. 43006558
Update: I had made a big mistake. Solved using this quora ans about KQUERY
my code with Order Statistics Tree, makes the code very simple: 43010933
can you pls explain the second parameter in order_of_key?
During the implementation I relized that a multiset is needed, in order to store more than one instance of key in the tree. So I gave every key anoter parameter that distinguishes it from the others and doesn't affect the order of the actual values.
It's a nice trick, if someone has a better solution to make it a multiset please share.
Great explanation, but I think I lost myself in some point. How this algorithm would work on this test case ?
3 0 -1 2 -3
The cumulative sum would be?
-1 1 -2
If yes, just in the -2 I would find 2 S[j] greater than -2. In the other two I don't find any.
The answer for this test case is 4.
NO, the partial sum, in that case, would be,
0, -1, 1, -2.
This might clear your doubt
you can also use a merge sort tree on prefix sums and binary search after.
i did that . but my soltuion failed on test case 8 . 43007201 [ UPD : Found my bug & Got ACCEPTED ]
can someone help me generate some hacks for my C solution 42986208 it looks quite similar to editorial
3 -1 -2 -3
In F, I get AC by following greedy algorithm but I don't know why it can get AC:
Let the center of the tree is vertex c.
Let the leaves are x1, x2, ...xm and dis(x1, c) ≥ dis(x2, c) ≥ ... ≥ dis(xm, c).
Can someone prove or disprove it >__<?
http://codeforces.com/contest/1042/submission/42991099
This seems to be O(n^2) worst case (calling f() multiple times), do you know why it isn't?
The time complexity of my solution is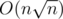 .
.
When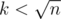 , each vertex will be visited at most k times because I write
, each vertex will be visited at most k times because I write
if(r<=ma[x])return;and ma[x] is range from 0 to k. Thus, the function f only visit k × n state.When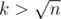 , a tree has at most O(n / k) leaves such that their distance is over k each other. So we only call function f at most
, a tree has at most O(n / k) leaves such that their distance is over k each other. So we only call function f at most  times.
times.
I use the tightest tests I can think out to test my program and it takes about 2.6 s in Codeforces to calculate the solution.
The greedy algorithm can be sped up to O(nlogn) using a segment tree http://codeforces.com/contest/1042/submission/43079231
I think it is correct.
In your algorithm, you find leaf x with maximum distance from the root c first. Which means one of the longest path of the tree must start at node x. We assume path(x, u) is the longest path of the tree.
Then, consider all y where dis(y, x) <= k. It is true that dis(y_i, y_j) <= k as well. Otherwise both dis(y_i, u) and dis(y_j, u) > dis(x, u) which is not possible.
Therefore, the beautiful set found by your algorithm should be valid. After you found one beautiful set, you ignore those nodes in further processing, which is similar to delete the subtree containing those nodes. Therefore, all the beautiful set found by your algorithm should be valid as well.
I get that the sets made by the algorithm are valid but why the total number of sets is minimum? You mean if our main vertex was not the center of the tree the algorithm would be correct either way? sorry if i asked a stupid question. sorry for my poor English.
Let the first node (the node use for comparing the distance) we pick for each set be x_1, x_2, x_3 ... x_m
According to the algorithm, It must be true that dis(x_i, x_j) > k otherwise they will be put to the same set. Therefore the algorithm should attain the optimal answer.
It was a stupid question I'm sorry. Thanks by the way.
IN array product my answer fails on 7 th test case . but i think my code is right.
Try this test case:
6
-8 -9 -7 2 3 0
yes. Now I got it.
my output for this test case is
1 5 4
1 3 6
2 6
1 1 2
1 2 4
which in turn equals to 432(-8*-9*2*3). but still i am not passing test case 7 . according to you what will be its answer?.
Try this: 3 -1 -2 -3
http://codeforces.com/contest/1042/submission/42995015
Please, Can someone see my solution? Codeforces says wrong answer but it is producing output as expected.
Your logic is incorrect, you are forgetting that you cannot move the people who have occupied the benches, hence not necessarily you can make equal people sit on all the benches to find the minimum.
I think your solution is wrong
Here is the sample 2 3 1 10
The answer is 10 13 Your code output 7 13
Cause the three people can sit on the second bench
So for each time where not all the people were sat , should find the min people of all bench and let this person sit here
( people who is already sat can not move , maybe you should read this problem again :)
Hope this can help you
Am I the only one who thought of DP at the first glance of B?
I also solved it using DP.
Can you please explain the solution and the dp state you chose, I couldn't understand your solution.
see mine, it should be easier to understand.
Your approach seems quite interesting. Can you please explain it? I could not figure it out. Just a brief explanation of what you did.
list the state in 3-bit binary number
if the state includes the bit 001 it means it contains vitamin A
if the state includes the bit 010 it means it contains vitamin B
if the state includes the bit 100 it means it contains vitamin C
The answer is ofc dp[(1 << 3) — 1].
The rest is just simply knapsack
This technique is called bitmask DP if ure interested
Cool, the dp solution in prob B is quite elegant in my opinion. I implement dp too, btw my implementation is quite awkward
Could anyone please explain for me the basic idea of F. It is not so vivid to me. I understand the technique here but the idea....
By the way, how to write the judge code for problem C? (I think this is not trivial.) Does anyone have an idea?
I can give you both checkers for this problem if you need :)
Oh, I missed the last paragraph of tutorial C (very sorry...!). And I'm interested in both checkers. Could you give me these sources...?
Here they are :)
Fourier
Multisets
Thank you very much! I like Fourier one :)
Why does this D solution gives TLE on 46 test case?
It seems that the complexity is O(N*logN*logN)
How? When I'm iterating with i, every time I call 2 log(4e14) functions. So complexity is O(2*N*log(4e14))=O(N*log(4e14)).
log(4e14)=14. Did I miss something?
In query(ll k) and add(ll k) functions, you used for loop in O(logN) time. For each k, you used map, the complexity was O(logN) time then total complexity for each function is O(logN * logN)
I have another solution for problem D(Petya and Array) which doesn't need any data structure and I think it is really easier. It's using the merge sort.
let the given array be a. we make array A such that A[0]=0 and for i>0 A[i]=A[i-1]+a[i-1]. (it's the partial sum!)
now we must find number of pairs i,j (0<=i<j<=n) such that A[j]-A[i]<t . now we run merge sort on array A this way:
explanation: in fact I am using divide and conquer. this algorithm at each time splits the given array into two arrays and counts the number of such pairs and sorts them. then it counts the number of pairs between the two sub arrays. and to count the number of pairs between two sub arrays it does the following: first we know the two arrays are sorted (we are using merge sort!); so we can use binary search on them! for each element A[i] in the first piece we can count the number of elements A[j] such that A[i]+t<A[j] using binary search!
time complexity of this algorithm is O(n * log^2(n)). my code: 43010896 It got AC in 156 ms. (I think if I have used scanf instead of cin it would be also faster) :)
It can be further reduced to O(n*logn) by calculation while merging. My Soln .
but your solution got AC in 233 ms and mine in 156 ms ;)
Because the constant factor of my algorithm is more than your algorithm. I copied elements and created more vectors than yours, whereas you have only swapped them. And for calculation of time complexity, we generally ignore constant factors.
Edit — I have removed some unnecessary commands including clock() and switch to array (which you have used) instead of vectors. Now it takes 124 ms.
Ok alishahali1382, I know you can do it in 123ms.
OK I was just kidding! :)
Can any one explain me what am I doing wrong in question C? I am continuously getting wrong answer verdict on test case 7.
My solution link is:-
http://codeforces.com/contest/1042/submission/43011863
Thanks in advance
If you have odd number of negative values and one zero element then you are multiplying all negative value with zero insted of just multiply maximum value of negative with zero and remove it. I think in this test case you are getting wrong answer.
Problem D: https://algotester.com/en/ArchiveProblem/Display/40362
About Problem E, what is the "real" answer for sample case 2 (that can be represented by a rational number P/Q?
It is .
.
There can be some paths, with their respective possibilities:
(1, 2) → (1, 1) — probability of , final score of 1
, final score of 1
(1, 2) → (2, 3) — probability of , final score of 2
, final score of 2
(1, 2) → (2, 1) → (1, 1) — probability of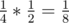 , final score of 3
, final score of 3
(1, 2) → (2, 1) → (2, 3) — probability of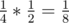 , final score of 6
, final score of 6
(1, 2) → (2, 2) → (1, 1) — probability of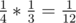 , final score of 3
, final score of 3
(1, 2) → (2, 2) → (2, 3) — probability of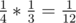 , final score of 2
, final score of 2
(1, 2) → (2, 2) → (2, 1) → (1, 1) — probability of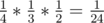 , final score of 3
, final score of 3
(1, 2) → (2, 2) → (2, 1) → (2, 3) — probability of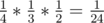 , final score of 6
, final score of 6
To summarize, the expected answer will be: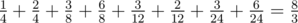 .
.
Hey Akikaze, can you tell me what evi is, in the tutorial of E?
Why can't we calculate for [r, c] all the possible jumps from it to all the elements with value < val[r, c]? we ((sum them up) / number of such elements < val[r,c])? And similarly for all the other elements < val[r, c], summing them up until we no more find element < val[i, j]?
(By summing them up, I mean summing the euclidean distance between them.)
Here is my code. Would be awesome if somebody cleared this doubt.
Failed on tooooo many troubles. Sad.
can someone explain the part in D's editorial how segment tree or fenwick tree can be used
For the problem D, anyone can explain more details for me please. What do we do when call upd(k)?
It's actually bad editorial. It's hard to understand ( cost me one day )
This is similar to the Inversion number problem, formally:
Given an integer sequence A which consists of N elements, count the number of pair (i, j) where i < j and A[i] > A[j] are satisfied.
It is known that this problem can be solved with BIT. The strategy is like:
The important part is A). if you count this value with straight forward algorithm, it will work in O(number of elements in S). To get this value efficiently, we can use BIT.
BIT provides these operations:
O(N) memory is required and both operation can be done in time (where N is max i).
time (where N is max i).
Treating A[j] as i, we can perform A) and C) operations using BIT, like A): get(A[j]), C): add(A[j], 1)
But there is a problem: A[j] can be big and it will cause MLE...
So, we have to pre-calculate k, such that A[j] is the k-th smallest number in A. (This can be done with sorting, unique the array and calling
lower_bound)After that, we can use k instead of A[j] for BIT.
This solution works in where N is the number of elements in A.
where N is the number of elements in A.
Can you provide the simpler code using BIT for this question D?
Solution (O(n log n)) has some problem for this data.
14 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14
this solution's answer is 2.
this is incorrect, yes?
There are two leafs(1 and 14) and distance between them is more than 1, so answer is 2.
thanks,I have a wrong Understanding for this question.
I solve D with wavelet tree, then realise the operation I use can be done with simple coordinate compression and fenwick tree.
It can also be done with merge sort tree
Problem F, the constant of O(n) solution is so large that the real runtime between O(n) and O(nlogn) is similar. (1076ms for O(n), 1091ms for O(nlogn))
Every time I read the editorials I think I need to put lot more effort
Problem D can be solved with STL's red-black tree implementation (https://codeforces.com/blog/entry/11080): http://codeforces.com/contest/1042/submission/43157263.
Can someone please tell me what is the bug in my code (http://codeforces.com/contest/1042/submission/43167869) for problem D. I used sqrt decomposition technique and am not able to find any bug myself. My logic is basically to find all the r>=l for every l.
You have to check whether
jis valid or not. (It is not guaranteed that(b+1)*Mis less thann+1)see: https://codeforces.com/contest/1042/submission/43174792
UPD: If you use g++, passing
-fsanitize=undefinedand-D_GLIBCXX_DEBUGoptions to the compiler makes it easier to detect these types of bugs (I found the bug just to try Sample Input 3. Please try it!)Thanks a lot and yes will use these in the future for detecting bugs.
In problem F, why the greedy algorithm is correct ?
In prob D: In pbds solution can anyone tell me why we need pair in ordered_set? I think it should be ok without pair. Details explanation would be great.
Thanks in advance :)
Since it is a set, if you store multiple same values it will get stored only once and you may lose exact count.
For D, Why does Multiset Time out?
in Problem F, a very important part of the proof is not mentioned in the editorial. Lemma: for each subtree, if $$$A$$$ and $$$B$$$ are any two sets which cannot be merged, then $$$dA+dB > k$$$. We can prove this by induction on height.
The reason this is an important part of the proof is that when we merge subtrees, we may ask, can't any other possible combination of sets be possible? It is not, because the lemma implies that the way to divide the leaves into sets is unique upto the height of the maximum element in the set ($$$dA$$$ and $$$dB$$$ can't be in the same set).
Even unoptimized $$$\mathcal{O}(N logN^2)$$$ solution can work comfortably in $$$1400$$$ ms: 160761034