Alright, so this is my 2nd post here. The 1st one, as you can see, was written in Vietnamese – my mother tounge, just because I thought that CodeForces Blog could be used for my personal purposes and my entry would not be read by anyone else, except me :D
Due to that, I’m gonna translate that post into English so that anyone can read it and leave feedbacks :) One more thing to say, *I’m not the original author of this article, I just rewrite it to understand BIT better *
PS: As I said, Vietnamese is my mother tounge, and I’m only a high school student, so sorry for my bad English. J
Advantages of BIT:
- Use less memory than RMQ
- Easy to code
- Can be used in many problems about number sequence
- Runtime: O(logN)
Disadvantages : =’= BIT is hard to understand (so that’s why I’m writing :D)
Main content:
BIT consists of two operations in an array A[1..N] of numbers
SET (index, value) : To add value to A[index] (or A[index] += value)
GET (index) : To sum up A[1]..A[index ] (or Get ≔ A[1] + … + A[index])
Details:
We know that a natural number can be expressed as a sum of the powers of 2, for example:
Example 1:
22 = 16 + 4 + 2
= 2^4 + 2^2 + 2 ^1
Applying this idea for BIT, we’re going to express the sum of A[1]..A[n] as a sum of sub arrays, each of them has 2^k elements
How to code:
S(i,j) is the sum of A[i]..A[j] (or S[i,j] = A[i] + A[i+1] +…+ A[j]). So with number 22 in Example 1, expressed as a sum of the powers of 2, is gonna be like this:
S(1,22) = S(1,16) + S(17,20) + S(21,22)
To get the positions of sub arrays, use this formula: i - i AND (-i) + 1.
Demo.:
22 - (22 AND (-22)) = 20
20 - (20 AND (-20)) = 16
16 - (16 AND (-16)) = 0
Thus, the structure of BIT T[] will be:
T[i]: Sum of S(i - i AND (-i) + 1 , i )
How does GET work?
Notice: GET (index) sums up A[1] → A[index].
Idea: To get the sum of A[1].. A[index], here we start with A[index] first. Parent of A[index] can be reached by using the following formula: i – i AND (-i)
GET (T,i)
1 s ← 0
2 while i > 0 do
3 s ← s + T[i]
4 i ← i – i and (-i)
5 return s
How does SET work?
Notice: SET (index,value) adds value units to A[index]
Idea: To increase the value of A[index] with value, is to increase sub arrays which CONTAINS A[index]
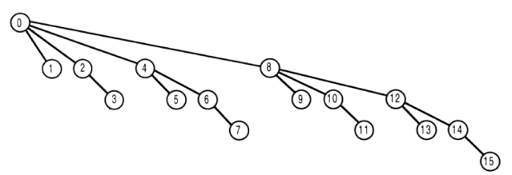
Example : We want to add 1 to A[9]. So we also have to add 1 to sub arrays which contains A[9]. Look at the image, here we have A[10], A[12] and A[16] both consist of A[9] J
So how do we find which array contains A[9]?
Use this formula: i + i and (-i)!
With this relationship, the demonstration of BIT will be opposed to the first one in GET procedure:

Pseudo-code
SET (T,i,v)
1 while i ≤ size[T] do
2 T[i] ← T[i] + v
3 i ← i + i AND (-i)










Well, a "binary indexed tree" is more general: exactly as the name says, its vertices (e.g. paths to them from the root) are, in some way, represented by the binary representation of their indices.
For example, one version of segment trees is binary indexed as well, when the root has number 1 and vertex i has sons 2i and 2i + 1, so the path root — vertex i is given by the binary representation of i, starting from the most significant 1 and up to the least significant bit.
A Fenwick tree just indexes the vertices in a special, compressed way.
BTW, it's called Finnish tree in Slovakia, I think the name stems from some Finnish olympiad that it appeared in once :D
6256. INVCNT
6294. YODANESS (same as INVCNT but string)
8002. HORRIBLE (BIT or segment tree)
2815. INCSEQ (DP + BIT)
1329. KPMATRIX (DP + BIT)
1029. MATSUM (BIT 2D)
when you want to update a..b += v , you can call update(a,v) and update(b+1,-v)
and when you want to know sum a..b you can call query(b)-query(a-1)
in query(p) function, you can do something like this :
res += bit[i][0];
res += bit[i][1]*(p-i);
i think it's easier than segment tree.. :D
I have a doubt in the update(a,b,v).Suppose N=8 i.e there are total 8 elements. Now update(3,6,10) will update(add 10 to) elements from index 3 to index 6. As mentioned above update(3,6,10) can be performed as update(3,10) and update(7,-10). update(3,10) adds 10 to indexes 3,4 and 8. Similarly update(7,-10) adds -10 to indexes 7 and 8.Now to find sum(6) which is the sum of all elements from index 1 to 6 , will be sum(5...6)+sum(1.....4) but index 5 and 6 were not updated. So I want to ask how is it giving the correct result?
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=binaryIndexedTrees
this tutorial have an example for BIT 2D but it's only the update proccess, but if you understand BIT, you could think and implement the query method.
http://e-maxx.ru/algo/fenwick_tree This one is nice, but it is in Russian.
You can now find the English version as well :)
https://cp-algorithms.com/data_structures/fenwick.html
I have searched and found that the update and query in case of 2D binary Indexed trees are simple and the code snippets are provided but there is nowhere given on how to initialize the 2D Tree array in that case. Could you please help me in this.
I found this site http://zobayer.blogspot.in/
It explains 1D,2D BIT with simple example :)
Simple yet nice explanation. Thanks a lot.