
On Oct/04/2018 10:05 (Moscow time), the Codeforces Round 513 by Barcelona Bootcamp (rated, Div. 1 + Div. 2) will start. This is a special round for the Hello Barcelona Programming Bootcamp, in collaboration with Moscow Workshops ICPC. It is rated for all participants, everybody can register on it regardless of a rating.
Hello Barcelona Programming Bootcamp is sponsored by VTB and Indeed Tokyo, with the addition of team sponsors Phaze Ventures, Spark Labs and REMY Robotics.
VTB, the largest international bank based in Eastern Europe, continues to be an official partner of the Hello Programming Bootcamp series, adding further quality to the 3rd edition of the Hello Barcelona Programming Bootcamp by bringing their own participants, as well as by supporting top teams from around the world.
Indeed Tokyo is Japan's branch of the #1 employment website in the world, giving job seekers free access to millions of jobs from thousands of company websites and job boards. As they sponsor for the second year in a row, Indeed continues to offer the best job opportunities to the boot camp participants.
Wish good luck to all the participants!
There will be 8 problems, common for both division. Score distribution: 500 750 1250 1500 1750 2250 2750 3000.
The problems are prepared by me, Arterm and GlebsHP, with assistance from 300iq, ifsmirnov and vintage_Vlad_Makeev. Have fun!











A good time for Chinese!
Unfortunately, bad time for me because of school
A bad time for Indians!
I forgot the contest time last time, so I may forget again. I don't want to lose a chance to get high rating!
Endagorion is there any chance that contest can be shifted one hour earlier or at standard codeforces contest time?? If possible please do so.
I am just sad about not getting to participate in the round i was waiting for over a week.
LUL
two contests back to back.
Thanks to MikeMirzayanov for polygon platform.
Please stop complaining about the inappropriate time of the contest for your country. Codeforces has to adopt different timings for other people. Not only for a specific country.
Right? Like, across US, India, China, and Russia, any time is going to be bad for somebody. What's the point in complaining?
Point of complaining as I think is that you cant participate cause of school/work. If contest would take place on weekend, people could even participate at night. But bad time + weekday is reason enough to complane
I wasn't complaining. I am just sad to miss the round by such good author & also this contest is after a long time from previous one. Neither I upvoted any comments who asked to shift the contest.
I wasn't aware "work" and "school" are specific countries, since that's going to be the main reason to skip this round for people in Europe, Africa and almost all of Asia. Then we have the Americas, where it's night. Ok, I guess it's a good time for New Zealand and Oceania.
It's also good for Japan, most of China, a part of Russia, South Korea and some other countries that actually does competitive programming. So it's a pretty good time for many people. About quarter of the earth can participate easily in any contest. It just depends in which quarter.
good time for those like me who has a day-off on thurdays!!!!!!
bad time for me, i have to poop at 10:30 AM..
This comment actually has more upvotes than the post itself.
Please no
If you cannot understand, it's IMO logo
that's time to participate in this contest after 2 weeks!
After a long duration Codeforces contest. Codeforces really awesome.
Sorry, you are on the wrong platform. Switch to Codeforc.
Upd:- Comment edited.
Switching is complete Now.
:D :D :D
Great time for me, 4AM so I get to wake up, do this contest and not miss any classes!
Is this a joke?)
No
I'm interesting, how you can get enough sleep before the contest
I don't :P
4:20 is much better
Миша, когда лекции??
Good time for those who skip classes for cf rounds
feeling happy :) ... hoping an interesting round :)
Hi! Is contest duration known? :)
Codeforces — Indeed the best interface for competitive programming
Bad time for me... had to compete Codeforces again...
Score distribution? Careless author.
What is the score distribution or is it acm style?
Bad time for Martians
My last year's Barcelona Bootcamp contest. Wish me luck this time :>
Can someone explain me solution for D, probably I am very stupid guy :)
On seeing AC solutions, the idea is the answer should be a total of n terms.Also we know only a l can reduce a r or vice versa. So now we take max l (assuming max l is morethan max r) and it should reduce max r ,anything other is suboptimal. Now we have two people combined so we can solve the problem further similarly.
So you want to say that since we can pair a "l" with every "r" as (a,b) and (c,d) can also be treated as (a,d) and (c,b) sitting on individual tables.
and since we want to take the summation_of(max(l,r)) for every pair and now , as we are allowed to replace their "r" as mentioned above . So, we will simply sort list individually.
Is this correct interpretation???
D was pretty neat. Basically, imagine everyone is at their own table originally. it is clear that the number of chairs used for a particular person i is max(li, ri) + 1. Imagine if we put two people at the same table, and say their values are (a, b) and (c, d) respectively. Through some inspection, we can see that this is equivalent to two people (a, d) and (c, b) sitting at their own individual tables*. This implies that we can permute the r values for all the pairs. From there it should be clear that we can minimize the chairs by sorting both the l and r arrays individually and calculating the number of chairs needed if these new sorted people were all at their own individual tables.
*To be more precise here, combining (a, b) and (c, d) results in 2 + max(a, d) + max(b, c) chairs, and leaving them alone results in 2 + max(a, b) + max(c, d) chairs. So the former case is equivalent to having two people of values (a, d) and (b, c).
Very nice solution, thanks for sharing it!
Nice explanation.
You can say that answer is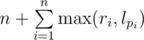 where pi is a person sitting next to i. Note that pi might be arbitrary permutation. Turns out, the best way to choose this permutation is make it so that lpi and ri are sorted in the same way.
where pi is a person sitting next to i. Note that pi might be arbitrary permutation. Turns out, the best way to choose this permutation is make it so that lpi and ri are sorted in the same way.
Just for my understanding of the solution can we find who sits right to whom?
Sure, pi sits right to i.
Thanks
But if pi is an "arbitrary permutation", this still doesn't answer who (in terms of l,r pairs given in input) sits next to who?
While sorting l and r, if you store the indices of the people along with the values, then the person corresponding to the value l[i] sits next to the preson corresponding to the value r[i].
(deleted)
I got it now, thanks!
I have a doubt here ... What if there are cycles in this permutation ? How do we interpret that ?
And how to prove the best way to choose the permutation is in that way ?
Nice problemset today (especially D), but the difficult from E to F is like from Div1B to Div1E...
How to solve it anyway?
How to solve F?
We iterate over every root and solve N problems independently. Let us call fixed root as r, and subtree of v as Tv.
DP[$v$][$k$]: Probability of survival of r, subject to the last contracted edge between r and v is contracted between k-th and k + 1-th contracted edge in Tv
We can calculate it by another DP. Total complexity seems O(N5), but like many tree DP, it is O(N4).
why I failed in Pretest 2( the same as the 2nd sample), but I still got the penalty?
You don't get penalty if only your program is wrong on pretest1
How to solve C?
1) sum(b[i],i=1..n) <= n * max(b[i]) ~~ 2000*2000 = 4*10^6 ,
2) let sb[z] — max( y2-y1+1), where sum(b[i], i = y1...y2) <= z. Precalc O(N^2)
3) answer = max( (x2-x1+1) * sb[X / sum(a[i],i=x1..x2) ] ), x1=1..n, x2=x1..n. O(N^2)
total complixity: O(N^2). with O(N^2) memory.
Is possible to solve C with binary search?
Actually I used, but I don't know whether it could be ACed yet.
I did it, then realize it was unnecessary, cause for both array, we could pre calculate the minimum sum for each range
I've read your code, maybe I have a different way. Here is my code (it has some bug) Here
hey, I solved it with binary search (C++'s built-in upper_bound)
The question can be converted into finding a subarray each from A and B such that product of sum of elements of those subarrays is less than or equal to x and the product of their size is maximum.
Pre-calculate the minimum sum continuous subarray of array A of each size from 1 to N. For all those minimum sum subarray of size from 1 to N, find the largest subarray in B which satisfies the above condition. It can be done using two pointers. Code: 43769883
As JustAni pointed out: "The question can be converted into finding a subarray each from A and B such that product of sum of elements of those subarrays is less than or equal to x and the product of their size is maximum."
Now, for both arrays we can calculate in O(n^2) the minimum sum achievable for interval sizes i=1..n, i.e. for array "a" we can calculate "a_min" as a_min[i] = min( sum(a[l]..a[r]) where r-l+1 = i), and the same can be done for array "b".
Now simply try all possibilities, track the current maximum and try to update it to i*j when a_min[i] * b_min[j] <= x. The time complexity of this step is sufficient, as it takes O(n*m), and the previous step took O(n^2) + O(m^2).
Nice and clean solution. THanks!!!!!!!
In problem D what is the answer to this test case : 2 10 10 1 1
I believe it is 13.
You're right Unfortunately I forgot this sentence : "You can make any number of circles" :(
Yeah, I had same problem to realize it for a 45 minutes, and after it I still couldn't solve on correct way :D
Should not one circle be sufficient for any case?
10 second... give me 10 second to submit F...
F
Could you please explain your solution?
http://codeforces.com/blog/entry/62199?#comment-461981
Already.
Probably I'm the only one who assumed C to be dp problem :(
I wasted 2 hours try to fit, from DP to Segment tree, through many other stuff, to C.
So how do you solve it?
How to solve E?
If you have path between two nodes in tree (a, b) equal to len, after adding extra edges in the tree it will be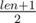 . So, for even paths it will be same as
. So, for even paths it will be same as  , for odd paths it will be for 1 bigger, i.e (
, for odd paths it will be for 1 bigger, i.e (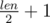 ). So, final answer will be
). So, final answer will be 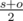 , where s is the sum of paths in the tree and o is the amount of odd paths in the tree.
, where s is the sum of paths in the tree and o is the amount of odd paths in the tree.
I understood it.Thanks!
Could you simply explain why it turns out to be
(len+1)/2after adding some extra edges?It's easy to convince yourself of this by making a few trees on paper (calculating sum of paths before/after extra edges and comparing).
How to count s?
let's say for an edge there are 'a' nodes on one side of the edge and 'b' nodes on the other side of edge also a+b=n, now this edge will contribute to a*b paths(think ) do this for every edge and add them finally you will get s. Now to find the o(i.e count of odd length paths in a tree ) we can use dp on trees .
In addition to allllekssssa's comment
1) Calculating s: First, you calculate subtree_size array, where subtree_size[i] is how much nodes do you have in a subtree rooted at "i" (or equivalently, number of descendants of node "i" + 1). You can calculate this array by first setting all values in array to 1, then computing the postorder traversal of the tree, and then iterating through nodes in postorder order updating that node's parent subtree_size with it's own (subtree_size[parent[node]] += subtree_size[node]).
Now, we can easily see that each edge is used exactly the number of times which we get by multiplying number of nodes on both sides of the edge. If we have the "subtree_size" array mentioned, we can simply traverse all the nodes except the root and update the "s" as follows: s += (n — subtree_size[node]) * subtree_size[node]
2) Calculating o: The path between two nodes will have odd number of edges iff they are on levels of different parity (level being the distance from the root). So, to calculate "o", calculate the number of odd-level nodes and the number of even-level nodes, and multiply them.
3) Solution = (s + o)/2
edit: nevermind, I misunderstood and I typed something dumb but I was wrong.
Oh, the prove is so detailed and beautiful. thanks a lot.
Thanks. This helped me immensely!
Nice <3
Thanks man!...You made my day
can you explain how the final answer will be (s+o)/2.
yeah overall ans seems to be (s/2 + o) but this will give error because of integer division property
firstly we know that(considering integer division) a/2 + b/2 =(a+b)/2 fails when both a&b are odd, and it works when both or at least one is even and for float division it is always true.
a/2=a/2-0.5(left side integer div , right side float div)
a/2+1=a/2+0.5. let divide paths into two sets s1(even length paths), s2(odd length paths) no problem is there when we combining the numerator of s1's terms but there is a problem with s2.
for s2 to combine terms of s2 we need to take effect and must add 0.5 for each term after combining,it become overall addition of 0.5*o.
hence it become overall s/2+0.5*o==(s+o)/2
you can check each property
What was pretest 9 in problem C?
I don't know what was the pretest, but after five WA at 9th pretest this is what I did and I passed it. "If you can take sum=10 with X ways then you can take every sum more than 10 with X ways as well. This means that you need to update your array like this arr[i] = max(arr[i], arr[i — 1])"
My approach was completely different than yours, so can you explain in more general terms.
My way was to precalculate all possible sums for array A and B. Now lets say X = 10. If we get sum from array A equal to 5(let say from elements 2 and 3), then we need to get a sum from array B equal to X / 5 = 2 or less. So the key here is the word "less". You don't care only for the value X/sum, but for all the values that are less than that.
I think this guy have cheated yuanmaoheng.
With whom? And how you got this info??
Let see his submissions in the past and compare it with this contest. Seem like he have known all the problems. 5 submits and got 5 ACed. Wow!?!
This is not a sufficient reason.
1. Especially when first 5 problems had ~500 submissions.
2. No extra lines are added in his code. And his code is Accepted not skipped which proves that his code does not match with someone else.
By this logic, tomorrow If I will solve 5 questions in Div2, then you will point me as a cheater.
I'm not commenting If he cheated or not. But the reason you mentioned is not at all sufficient to doubt if he is guilty.
Fyi, Skipping solutions (ie Plagiarism detection) takes place after system testing.
There are many reasons for submissions of several problems in quick succession, like power-cut, network-dropdown or something.
You can still think without power/network coverage, please.
When the next Div.3 round is going to be?
my level of regret for trying D instead of C is over 9000
Is it legal that leave a special case for hacking. http://codeforces.com/contest/1060/submission/43777486
I made a very funny bug in D. Instead of an easy solution with sorting both arrays independently I overdid and created two sets with pairs (one ordered by first component and the other by second component). As in easier solution I considered maximum of first components and maximum of second components. But when considering two pairs (l_max, r_not_max) and (l_not_max, r_max) I wrote a code removing both them from sets and inserting an element (l_not_max, r_not_max) (like we placed two people with corresponding segments alongside). Of course, if two pairs are the same we don't have to insert anything — we just remove this pair from both sets.
When checking if actually two pairs are the same I did stupid mistake and wrote an always-true condition.
But it appeared that this mistake didn't ruin the solution. When we simply remove maximal elements from both sets we have a situation similar to a one with two independently sorted arrays (as in easier solution). After the contest my friend showed me this mistake and I was upset because didn't realize that easier solution works. But surprisingly it got AC, and now I understand why :)
Even though I did not perform well today, I will probably remember this round as I hacked a solution with an anti-quicksort testdata.
Today Chinese guys did so great. There were 4 Chinese in top 5, 7 Chinese in top 10 and 13 Chinese in top 20. How do you guys train?
sunset TLE whzzt fateice AwD xumingkuan ugly2333 yhx-12243 yfzcsc Tommyr7 orbitingflea zhangzy cz_xuyixuan
There must be a secret technique. ;)
Maybe the time is good for Chinese?
It was because of the timing. The contest started at 15:00 in China during the National Day vacation, when almost everyone can participate with full energy.
The only thing is this round was held in the afternoon in UTC+8 and others were mostly at midnight.
China needs new online judge like codeforces
Do you know UOJ and LOJ?
I'll just post this good old meme here.
Because they accepted thousands of hard problems.
You are just a Specialist. YOU ARE NOT EVEN QUALIFIED TO JUDGE IT!
can anyone will tell me the approach for problem B ? thanks in advance .....
Any digit (except for the first one and any nines that may appear) in the number n can result either from simple addition (d1 + d2 = dn) or addition with "carrying" (d1 + d2 = 10 + dn. So one possible solution is to check all bitmasks from 00...00 to 11...11 where 0 denotes that a certain digit is produced by simple addition and 1 that it was produced by "carrying" with taking care to discard masks that have 1 in a position where there''s a 9 followed by a 0.
However, simply adding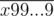 to
to 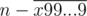 seems to work.
seems to work.
For a,b what matters is the sum of digits (and not the number itself) and for max sum have as many 9's in a as possible.
So number of number that a can be 10 * (number of digits in n).
Permute through all a's such that a < n and b = n-a and the find max(S(a)+S(b)).
Link to my solution:43764388
Though there were easy number theories for this problem, don't know why the idea of digit dp hit my mind. My solution using digit dp was not very complex though. Just construct every number a less than n and store maximum s(a)+s(n-a) in the dp table.
My solution: 43766071
How to solve D?
First sort l[] and r[]. Then iterate from reverse direction — if(l_i and r_i are of different person) then add max of them to answer because we can place them on adjacent places and left of one will be right of other. if(l_i & r_i are of same person) then form new group and add max of l_i and r_i to answer.
Thanks!
I wonder if there will be a tutorial? Or has it not come yet?
I have been refreshing this blog page since last two hours to check for Tutorial update. Don't tell me there will be no tutorial.
where is the editorial?
Problems were good. Eagerly waiting for the Editorial for some up-solving.
Could you tell me where i can get the editorial? I can't understand the O(n^2) algorithm of C.
PS:It seems that D is much easier than C.I use skytyf this account in this contest and get 3 problems except C. --Sorry for my poor English :)--
It seems that if you could not solve D quickly, then it would be really difficlt... I solved A to E except D :( For me, the algorithm for C is more familiar.
Problem D is great! But I was too stupid to solve it in the contest:(
Could you share the tutorial?
How does D work? I still don't understand the solutions. Will there be a formal proof for this sorting method? For some reason I can't convince myself that it's correct...
Not a formal proof but it's how I visualized it and maybe you can at least convince yourself:
Imagine at the start, every person's a bead with a LHS end and a RHS end, and that we're linking the people together, one link at a time, into chains (that eventually links its ends together into cycles). From now, we MUST perform exactly N links to join all the unpaired ends and minimize the cost.
Let's take the guy with the highest unpaired RHS or LHS cost. Let's say that it was a RHS cost that was larger than everything else, and let's call the cost V (if it was LHS it will be symmetrical). This person's RHS MUST be linked with somebody's LHS (maybe even his own). He can be linked with any available LHS, but who should he be linked with? Since V is >= any LHS cost, any linking is going to cost V anyway. So, you might as well pick the guy with the highest LHS cost, to "absorb" the biggest cost possible. It's the best choice, since if we picked a different LHS, the remaining links we must do would be EXACTLY the same except now one of the LHS elements is more costly, which is clearly less desirable. Now again consider the largest RHS or LHS cost of the remaining unpaired ends, and repeat the linking process.
If you visualize this, you will see multiple chains that start growing and joining, and sometimes the chains close into cycles when the RHS of a chain links with the LHS of itself.
Clearly, to implement this method, you will just iterate through the sorted lists of RHS and LHS costs one by one, linking them.
To think of it another way, the final result is a permutation, P(i) = j where the i'th person has the j'th person on the right hand side. Look at what happens when you start at a person and go left to right, following the permutation — the circles of the seating are the cycles of the permutation.
Very nice explanation
My solutions to some of the harder problems:
E: recursive DP. If the distance from u to v in the original was d, it is now ceil(d/2). Within a subtree, keep track of
With this information, one can link a new subtree to a parent in O(1) time. There are four cases, and in each case you can compute the sum of lengths of all paths through the new edge, as well as how much to add to account for the ceil().
F: we'll solve separately for each query (fortunately N is small to we don't need to be too careful about efficiency). Place the query node at the root. Now consider some subtree. For the first few shrinks, it won't matter which label is chosen, but at some point this subtree will be rooted at the root of the whole tree and then any shrink involving the root has to pick the root label. So we can use DP to answer this question for each subtree and each K: if the first K shrinks are "safe", what is the probability that the shrinks won't eliminate the root? We start from the leaves, and build up a tree using two operations; 1. Add an edge above the old root. To answer this, we need to consider each possible position this new edge can have in the sequence of shrinks of the subtree. 2. Join two trees together at the root. In this case the events in the trees are independent, but he have to consider all possible partitions of the safe shrinks between the two trees.
H: I had an algorithmically correct solution to this, but just ran out of time debugging it (I wasted a lot of time before reading that the other cells contained 1, not 0). Since we can add numbers, we can multiply a number by any constant, and we can do it in log time using the same trick normally used for fast exponentiation. That also means we can divide by a constant (just multiply by the inverse mod p), we can construct 0 (multiply anything by p) and negate numbers (multiply by -1).
We can compute xd, (x + 1)d, (x + 2)d, ..., (x + d)d, and express each as a linear combination of 1, x, x2, x3, ... xd. The resulting matrix can be inverted to allow any xi (0 ≤ i ≤ d) to be expressed as a linear combination of (x + j)d (0 ≤ j ≤ d).
This means that we can square numbers, and since xy = ((x + y)2 - x2 - y2) / 2, we're done.
A few different solutions for problems E and H:
E: Each path of length d becomes a path of length . This means the total sum of paths is equal to (sum of all path lengths + # of paths of odd length) / 2.
. This means the total sum of paths is equal to (sum of all path lengths + # of paths of odd length) / 2.
Sum of all path lengths can be computed quickly by noting that each edge is crossed exactly sizeleft * sizeright times, where sizeleft and sizeright are the sizes of the two subtrees on either side of the edge. Number of paths of odd length can be computed similarly -- it's just nodd * neven where nodd and neven are the number of nodes with odd and even depth from the root, respectively.
H: Consider the polynomial (a1 + a2 + ... + aD)D. It contains the term D!a1a2...aD as well as lots of other extraneous terms. Inclusion-exclusion on the D-th powers of each subset sum of ai leaves just this D!a1a2...aD term (since it's the only term that encompasses all D elements ai). Now apply this idea with a1 = x, a2 = y, a3 = a4 = ... = aD = 1 and you're done :)
Really interesting to see this strategy in H of obtaining x2 from x. From looking at a few other contestants' solutions it looks like most people followed this route -- curious how you all thought of the idea!
Nice solution to E.
On H, I wonder if your solution was the intended one — it would explain the very low constraint on D, since your solution takes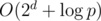 operations, whereas mine takes
operations, whereas mine takes 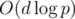 . As to how one thinks of it, I started with (x + y)d as the obvious way to get products of x and y, and then saw that as long as d=2 it would work out easily.
. As to how one thinks of it, I started with (x + y)d as the obvious way to get products of x and y, and then saw that as long as d=2 it would work out easily.
No, O(2d) solution was not expected,
could you describe it?(I see you already did.) The constraint for d was kinda random.You can came to x2 idea by setting x = y. The reason we made no samples was to hide this idea, because it's quite apparent even from case d = 2, p = 3.
For E is it possible to do ceil(ans/2) instead of counting odd and even? Thanks in advance.
Nope, let's say there are 3 paths of length 3 in the original tree, after adding the edges they would become 2, so 6 in total. ceil(9/2)=5
Oh I see, Thanks!
How to proof that the coefficients of xd, (x + 1)d, ..., (x + d)d are linearly independent under modulo p?
That's a good question. It's something I remember (at least for the real numbers, and I just trusted it would also work out in the field mod p), but I can't think of a proof at the moment.
If you look closely at Lagrange interpolation formula, you'll see it works while d < p.
Alternatively, if you put coefficients in a d + 1 × d + 1 matrix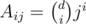 , one can see it is (almost) Vandermond's matrix, and its determinant can be calculated directly.
, one can see it is (almost) Vandermond's matrix, and its determinant can be calculated directly.
Where is the editorial?
It's dead .
The editorial is very funny.
Where is it ? Has it been released ?
i am new to BST. can anyone tell me the source or links for basic questions on BST for practice ? thanks in advance...
BSTs are usually asked in Interview questions rather than competitive programming.
I think Hackerrank here has a really good collection of BST questions.
Well I've waited for the editorial for a whole day...
Well I have waited the editorial for four whole days.
Well I have waited the editorial for 18 months.
Well I have waited for the editorial for 30 months
Well I have waited for the editorial for 52 months.
Well, I have waited for the editorial for wait my memory seems fuzzy now
https://codeforces.com/blog/entry/113725
Nice, it came out. Thanks
When you see this comment,you have wasted lots of time waiting the dead editorial.
Does anybody know where the tutorial is?
I think there won't be. Because last year's round by Barcelona Bootcamp doesn't have tutorial.
where is the Tutorial? I'v been waiting for several days!
I want to know how to solve F and H!
Do we have the editorials yet?
Why is there no tutorial?
because they are pigeons.