persistent_try's blog

Is information lost?
By persistent_try, history, 5 years ago, In English

As for many combinatorial etc. tasks we choose to perform %(mod) operation with a prime no.(M) but is the information lost?i.e Can we map back to the orignal no of combinations whose max value we actually restricted to M.

Extra question:

In the given image while calculating %p for each why is np%p=1 {n=1,2,3,4.. } instead of 0.

  • Vote: I like it
  • -3
  • Vote: I do not like it

Comments Comments (2)
| Write comment?
»
5 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

RE: retrieving the original value x before applying the mod operator

This is only possible if the quotient is stored. Suppose that . Then, x should be expressed in terms of p, q and r as

x = q × p + r

If q is lost, then the exact value of x cannot be computed, even though we know that it should satisfy the previous equation.

RE: computing n!%p when n ≥ p

Yes, I think that there is an error in this image.

for any integer k ≥ 1.

Therefore,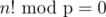 when n ≥ p.

→ Reply
»
5 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Yes, in general this information is lost. Usually there are infinitely many different outcomes for a combinatorics problem, e.g. every positive integer, or every factorial value, and all of those outcomes are mapped into the range [0, M - 1]. Of course some of the possible outcomes will get mapped to the same values in the range, and it is impossible to find out which of these outcomes was the correct one without additional information.

Now, with additional information it might be possible. But to answer that one, you have to ask a more precise question. Just to show that you need a lot of information: .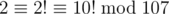

To the picture: Everything is correct. The picture doesn't say that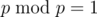 . If you read the definition in the sentence above, you would realize that this actually doesn't compute , but a modified version of it. Quote: "You want to calculate n!modp, without taking all the multiple factors of p into account that appear in the factorial. Imaging you write down the prime factorization of n!, remove all factors p, and compute the product modulo p. "

→ Reply