some days ago I have found a stronger version of an old problem: TCO 13 round 3A 1000pts:
https://community.topcoder.com/stat?c=problem_statement&pm=12547 stronger version: https://www.lydsy.com/JudgeOnline/problem.php?id=3284 with range m-n<=1000
but I have found this stronger version is not strong enough..I have found (m-n)*lg(m-n) sol of this problem.. the problem is to compute number of sol X1+X2+..+Xm<=s
satisfy 1:1<=i<=N,Xi<=t 2:X1+X2+...+Xm<=s the answer is sigma C(S-X1-X2-..XN,M-N) for each 1<=i<=n xi<=t the answer can be write as (f[0]*z^0+f[1]*z^1+...+f[m-n]*z^(m-n))/(m-n)! z==S-X1-X2-...-XN-(m-n). and f[] is the stirling number of first kind.
we have two steps first to compute the stirling number of first kind and second is to compute sigma((S-x1-x2-..-xn)^i) xi from 1 to t,for each i =1 to m-n
the expansion of (S-x1-x2-...-xn)^i is sigma(i!/(i1!*i2!*..in!*in+1!) (-x1)^i1(-x2)^i2*..*(-xn)^in*(S)^in+1) xi is from 1 to t, i1+i2+..+in+1==i i is from 0 to m-n. if g[i]=1^i+2^i+...+t^i.
if h(x)==simga(g[i]*x^i/i!) ,g(x)==sigma(S^i*x^i/i!). then g(x)*h(x)^n is generation funtion of (S-x1-x2-..-xn)^i we can compute g(x)*h(x)^n by g(x)*exp(n*ln(h(x)), this is (m-n)*lg(m-n)
and how to get g[i],i from 0 to m-n we know an (m-n)^n sol can get g[i]: (t+1)^(i+1)-t^(i+1)==simga(C(i+1,i+1-j)*t^j) j is from 0 to i. t^(i+1)-(t-1)^i==sigma(C(i+1,i+1-j)*(t-1)^j) j is from 0 to i ... 2^(i+1)-1^(i+1)==simga(C(i+1,i+1-j)*1^j) j is from 0 to i
and these equations we can get t^(i+1)-1== sigma(C(i+1,i+1-j)*g[j] j is from 0 to i so g[i]==(t^(i+1)-1-sigma(C(i+1,i+1-j))*g[j])/(i+1) j is from 0 to i-1.
if you continue to expansion this equation you can get:
g[i]==simga(i!/((-(i1+1))!*(-(i2+1)!)*(-(i3+1)!)*..*(-(ik+1)!))*(t^(i(k+1)+1)-1)/((i(k+1)+1)! k is from 0 to +oo i==i1+i2+..+i(k+1) if we set f(x)==x^i/(-(i+1)!) g(x)==(t^(i+1)-1)/(i+1)! then g[i]'s generation funtion is g(x)/(1-f(x)) . then we can find g[i] by compute inverse of(1-f(x) and multiply it by g(x).. so g[i] can be compute (m-n)*lg(m-n)
last how to compute stirling number of find kind by (m-n)*lg(m-n)?
just use recursion if we have found coef o f(n/2,x)=(x+1)*(x+2)*..*(x+n/2) then we can got f(n,x)==f(n/2,x)*f(n/2,x+n/2) we can expansion f(n/2,x+n/2) using FFT in O(n*lg(n)) and find multiply using FFT in O(n*lg(n)) so complexity is T(n)=T(n/2)+O(n*lg(n)) it is O(n*lg(n))
so total complexity of this problem is O((m-n)*lg(m-n).
here is implement of this problem










It would look better if you used LaTeX instead.
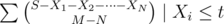 .
.
For example:
sigma C(S-X1-X2-..XN,M-N) for each 1<=i<=n xi<=tcan be written as\sum \binom{S - X_1 - X_2 - \dots - X_N}{M-N} \mid X_i \leq twith two dollar sign surrounding it. Which will be displayed as: