Tutorial is loading...
Code (by arsijo)
#include <bits/stdc++.h>
using namespace std;
int main(){
int a, b, c;
cin >> a >> b >> c;
cout << min(a + 2, min(b + 1, c)) * 3 - 3;
}
Tutorial is loading...
Code
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
int main() {
int N; cin >> N;
vector<pii> O(N), T(N);
for (int i = 0; i < N; i++) cin >> O[i].x >> O[i].y;
for (int i = 0; i < N; i++) cin >> T[i].x >> T[i].y;
sort(O.begin(),O.end());
sort(T.begin(),T.end());
reverse(T.begin(),T.end());
vector<pii> Ans(N);
for (int i = 0; i < N; i++) Ans[i] = {O[i].x+T[i].x, O[i].y+T[i].y};
sort(Ans.begin(),Ans.end());
cout << Ans[0].x << ' ' << Ans[0].y << endl;
}
Tutorial is loading...
Code
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
int main() {
ll N; cin >> N;
vector<ll> ans;
for (ll i = 1; i*i <= N; ++i) {
if (N%i==0) {
ans.push_back(N*(i-1)/2 + i);
if (i*i!=N) {
ans.push_back(N*(N/i-1)/2 + N/i);
}
}
}
sort(ans.begin(),ans.end());
for (int i = 0; i < ans.size(); ++i) {
cout << ans[i] << " \n"[i==ans.size()-1];
}
}
Tutorial is loading...
Code
#include <iostream>
#include <vector>
using namespace std;
template <unsigned int N> class Field {
typedef unsigned int ui;
typedef unsigned long long ull;
inline ui pow(ui a, ui p){ui r=1,e=a;while(p){if(p&1){r=((ull)r*e)%N;}e=((ull)e*e)%N;p>>=1;}return r;}
inline ui inv(ui a){return pow(a,N-2);}
public:
inline Field(int x = 0) : v(x) {}
inline Field<N> pow(int p){return (*this)^p; }
inline Field<N> operator^(int p){return {(int)pow(v,(ui)p)};}
inline Field<N>&operator+=(const Field<N>&o) {if (v+o.v >= N) v += o.v - N; else v += o.v; return *this; }
inline Field<N>&operator-=(const Field<N>&o) {if (v<o.v) v -= o.v-N; else v-=o.v; return *this; }
inline Field<N>&operator*=(const Field<N>&o) {v=(ull)v*o.v % N; return *this; }
inline Field<N>&operator/=(const Field<N>&o) { return *this*=inv(o.v); }
inline Field<N> operator+(const Field<N>&o) const {Field<N>r{*this};return r+=o;}
inline Field<N> operator-(const Field<N>&o) const {Field<N>r{*this};return r-=o;}
inline Field<N> operator*(const Field<N>&o) const {Field<N>r{*this};return r*=o;}
inline Field<N> operator/(const Field<N>&o) const {Field<N>r{*this};return r/=o;}
inline Field<N> operator-() {if(v) return {(int)(N-v)}; else return {0};};
inline Field<N>& operator++() { ++v; if (v==N) v=0; return *this; }
inline Field<N> operator++(int) { Field<N>r{*this}; ++*this; return r; }
inline Field<N>& operator--() { --v; if (v==-1) v=N-1; return *this; }
inline Field<N> operator--(int) { Field<N>r{*this}; --*this; return r; }
inline bool operator==(const Field<N>&o) const { return o.v==v; }
inline bool operator!=(const Field<N>&o) const { return o.v!=v; }
inline explicit operator ui() const { return v; }
inline static vector<Field<N>>fact(int t){vector<Field<N>>F(t+1,1);for(int i=2;i<=t;++i){F[i]=F[i-1]*i;}return F;}
inline static vector<Field<N>>invfact(int t){vector<Field<N>>F(t+1,1);Field<N> X{1};for(int i=2;i<=t;++i){X=X*i;}F[t]=1/X;for(int i=t-1;i>=2;--i){F[i]=F[i+1]*(i+1);}return F;}
private: ui v;
};
template<unsigned int N>istream &operator>>(std::istream&is,Field<N>&f){unsigned int v;is>>v;f=v;return is;}
template<unsigned int N>ostream &operator<<(std::ostream&os,const Field<N>&f){return os<<(unsigned int)f;}
template<unsigned int N>Field<N> operator+(int i,const Field<N>&f){return Field<N>(i)+f;}
template<unsigned int N>Field<N> operator-(int i,const Field<N>&f){return Field<N>(i)-f;}
template<unsigned int N>Field<N> operator*(int i,const Field<N>&f){return Field<N>(i)*f;}
template<unsigned int N>Field<N> operator/(int i,const Field<N>&f){return Field<N>(i)/f;}
typedef Field<998244353> FF;
int main(int argc, char* argv[]) {
int n; cin >> n;
auto F = FF::fact(n);
auto I = FF::invfact(n);
FF ans = n * F[n];
for (int i = 1; i < n; ++i) ans -= F[n]*I[i];
cout << ans << endl;
}
Tutorial is loading...
Code
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
#define MAXN 500000
int N;
int A[MAXN];
long long sum;
#define TOO_SMALL -1
#define OK 0
#define TOO_BIG 1
int is_score(int value) {
vector<int> C(N+1,0);
for (int i = 0; i < N; ++i) ++C[A[i]];
++C[value];
int less = 0;
long long left = 0, right = 0;
for (int k = 0, i = 0; k <= N; k++) {
int val = (i == k && (i == N || A[i] < value)) ? value : A[i++];
left += val;
--C[val];
right -= min(val, k);
less += C[k];
right += N-k-less;
if (left > right + (long long)(k+1)*k) {
return (i == k) ? TOO_BIG : TOO_SMALL;
}
}
return OK;
}
int main(int,char**) {
ios_base::sync_with_stdio(false);
scanf("%d", &N);
sum = 0;
for (int i = 0; i < N; i++) {
scanf("%d", A + i);
sum += A[i];
}
sort(A,A+N,greater<int>());
int parity = sum & 1;
int lo = 0, hi = (N - parity) / 2, lores = -1;
while (lo <= hi) {
int mid = (lo + hi) / 2;
if (is_score(2*mid + parity) == TOO_SMALL) {
lo = mid + 1;
} else {
lores = mid;
hi = mid - 1;
}
}
lo = lores;
hi = (N - parity) / 2;
int hires = -1;
while (lo <= hi) {
int mid = (lo + hi) / 2;
if (is_score(2*mid + parity) == TOO_BIG) {
hi = mid - 1;
} else {
hires = mid;
lo = mid + 1;
}
}
if (lores == -1 || hires == -1) printf("-1\n");
else {
for (int i = lores; i <= hires; ++i) printf("%d ", 2*i+parity);
printf("\n");
}
}
Tutorial is loading...
Code
#include <iostream>
#include <vector>
#include <string>
typedef long long ll;
using namespace std;
int main() {
int N; cin >> N;
vector<ll> L(N);
for (ll &l: L) cin >> l;
string T; cin >> T;
bool hadWater = false;
ll time = 0, stamina = 0, twiceGrass = 0;
for (int i = 0; i < N; ++i) {
if (T[i] == 'L') {
time += L[i];
stamina -= L[i];
if (stamina < 0) {
/* not enough stamina, walk or swim "in place" to gain it */
time -= stamina * (hadWater ? 3 : 5);
stamina = 0;
}
} else if (T[i] == 'W') {
hadWater = true;
stamina += L[i];
time += 3 * L[i];
} else {
stamina += L[i];
time += 5 * L[i];
twiceGrass += 2*L[i];
}
/* no more than stamina/2 of walking can be converted to flying to save time,
* otherwise there would not be enough stamina at this point */
twiceGrass = min(twiceGrass, stamina);
}
if (stamina > 0) {
// convert walking to flying
time -= (5-1) * twiceGrass/2;
// convert swimming to flying
time -= (3-1) * (stamina - twiceGrass)/2;
}
cout << time << endl;
}
Tutorial is loading...
Code (by winger)
import random
def isPrime(n):
"""
Miller-Rabin primality test.
A return value of False means n is certainly not prime. A return value of
True means n is very likely a prime.
"""
if n!=int(n):
return False
n=int(n)
#Miller-Rabin test for prime
if n==0 or n==1 or n==4 or n==6 or n==8 or n==9:
return False
if n==2 or n==3 or n==5 or n==7:
return True
s = 0
d = n-1
while d%2==0:
d>>=1
s+=1
assert(2**s * d == n-1)
def trial_composite(a):
if pow(a, d, n) == 1:
return False
for i in range(s):
if pow(a, 2**i * d, n) == n-1:
return False
return True
for i in range(20):#number of trials
a = random.randrange(2, n)
if trial_composite(a):
return False
return True
def gcd(x, y):
return x if y == 0 else gcd(y, x % y)
n = int(input())
divs = [n]
def split(parts):
global divs
divs = [gcd(d, p) for d in divs for p in parts if gcd(d, p) != 1]
while not all([isPrime(x) for x in divs]):
x = random.randint(0, n - 1)
g = gcd(n, x)
if gcd(n, x) != 1:
split([g, n // g])
continue
y = int(input('sqrt {}\n'.format(x * x % n)))
if x == y:
continue
a, b = abs(x - y), x + y
g = gcd(x, y)
split([a // g, b // g, g])
print('!', len(divs), ' '.join(str(d) for d in sorted(divs)))
Tutorial is loading...
Code
#include <vector>
#include <stack>
#include <iostream>
#include <algorithm>
#include <bitset>
using namespace std;
typedef unsigned int ui;
typedef long long ll;
struct Sieve : public std::vector<bool> {
// ~10ns * n
explicit Sieve(ui n) : vector<bool>(n+1, true), n(n) {
at(0) = false;
if (n!=0) at(1) = false;
for (ui i = 2; i*i <= n; ++i) {
if (at(i)) for (int j = i*i; j <= n; j+=i) (*this)[j] = false;
}
}
vector<int> primes() const {
vector<int> ans;
for (int i=2; i<=n; ++i) if (at(i)) ans.push_back(i);
return ans;
}
private:
int n;
};
constexpr int M = 2e5;
auto P = Sieve{M}.primes();
int main() {
ios_base::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
vector<int> G(M, 0);
int Q = P.size();
for (int i = 0; i < Q; ++i) {
for (int j = i; j < Q; ++j) {
if (ll(P[i])*P[j] >= M) break;
P.push_back(P[i]*P[j]);
}
}
bitset<M> PB;
for (int p : P) PB[p] = true;
int N, F; cin >> N >> F;
PB[F] = false;
vector<bitset<M>> W(100);
W[0] = PB;
for (int i = 1; i < M; ++i) {
while (W[G[i]][i]) G[i]++;
W[G[i]] |= PB << i;
}
cerr << *max_element(G.begin(),G.end()) << endl;
int g = 0;
for (int i = 0; i < N; i++) {
int r,w,b;
cin >> r >> w >> b;
g ^= G[w-r-1];
g ^= G[b-w-1];
}
if (g == 0) {
cout << "Bob\nAlice\n";
} else {
cout << "Alice\nBob\n";
}
}











1091A Tutorial is not available
not
Dude it's 9 days ago, how could you not notice that?
It was fast :D
I haven't seen such fast editorial! Cool contest, I enjoyed it!
Happy New Year!
Problem D: How do you prove that, there are no pair of indices (i, j) such that sum of [i, j] is n(n + 1) / 2 and [i, j] is not a permutation of 1, 2, ..., N ?
Hi, when N = 5 there is a subsequence 1, 5, [4, 3, 2, 2, 1, 3], 4, 5 and there is subsequence of length 6 and sum 15, isn't it?
The length of that subsequence should be equal to N
Thanks, I completely overlooked that.
If (i,j) is just one of n! permutations it is obvious permutation. Lets call (i,j) substring. It has k characters as suffix of some permutation and n-k characters as prefix of NEXT permutation. This k first characters of our substring: a) If they are not in decreasing order we then the next permutation will only differ on last (or less)k characters which implies the fact that n-k first characters of next permutation are same as in this permutation before. So, indeed if this k characters are not in decreasing order we obtain substring (i,j) which is permutation of numbers 1,2,3..n. b) Second option is that first k characters of our substring are the suffix of before permutation and they are all in decreasing order. Then, we cannot actually obtain substring starting with this k characters. Why? This is about the thing that last k characters will differ in before and next permutation by exactly one letter, which implies that their prefixes of length n-k will differ exactly by one letter too. I know how to prove it when k is the longest decreasing suffix. Then it is pretty clear. In other case(k is decreasing suffix but not longest) i think that something similar is true. The proof when k is the longest decreasing suffix comes from algorithm for generating all permutations in lexicographical order. Im sorry for my poor english. Let me know if something is unclear or if im wrong somewhere.
I think the following is pretty unreasonable to come up with in contest...
We will show inductively that for any consecutive permutations σ, σ + 1, if the sum of the first k elements are the same, the first k elements must be permutations of each other. Let σ = (a1, ..., an), σ + 1 = (b1, ..., bn).
Let k be the length of the longest common prefix of σ, σ + 1, and let m < n be maximal such that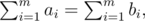 and for now assume k > 0. The key idea is that (ak + 1, ..., an), (bk + 1, ..., b2n) are consecutive permutations. Thus if k < m, we have ak + 1 + ... + am = bk + 1 + ... + bm which by the inductive hypothesis implies that ak + 1, ..., am are a permutation of bk + 1, ..., bm, contradicting the maximality of k.
and for now assume k > 0. The key idea is that (ak + 1, ..., an), (bk + 1, ..., b2n) are consecutive permutations. Thus if k < m, we have ak + 1 + ... + am = bk + 1 + ... + bm which by the inductive hypothesis implies that ak + 1, ..., am are a permutation of bk + 1, ..., bm, contradicting the maximality of k.
We now take care of k = 0. Clearly σ = (a1, a2 > a3 > ... > an) and σ + 1 = (a1 + 1, b2 < b3 < ... < bn). Then it is clear that the prefix sums of length > 2 are greater for σ than σ + 1. For length 2, equality only holds if the biggest number in (1, ..., n) is one more than the smallest, i.e. n = 2 which is checked by hand.
With his lemma, we can show that if a contiguous interval of length n has sum n(n + 1) / 2, it must be a permutation of 1, ..., n. Indeed, let this contiguous interval be lodged between two consecutive permutations (c1, ..., cn), (cn + 1, ..., c2n). Then which by the lemma implies that (cn + 1, cn + 2, ..., cn + k) is a permutation of (c1, ..., ck). Thus
which by the lemma implies that (cn + 1, cn + 2, ..., cn + k) is a permutation of (c1, ..., ck). Thus  as permutations, as desired.
as permutations, as desired.
There is few flaws in this proof.
This induction implies that in inductive hypothesis, (a1 , ... , an) and (b1, ... , bn) don't need to form a permutation of consecutive numbers.
Then in this statement, σ + 1 might not begin with a1 + 1. It can be some other numbers in (a2, a3 , ... , an) which is greater than a1.
Besides, I don't think it is clear that the prefix sums of length > 2 are greater for σ than σ + 1. Maybe it needs some further proof. Sorry for my poor intelligence.
I'm not sure that I understand what you mean by the first point. What I'm using is that if two consecutive permutations have a common prefix of positive length, the remaining parts of the permutations are consecutive permutations of each other. For example 21354 -> 21435.
I didn't explain the k = 0 case in much detail. The fact that σ + 1 must start with a1 + 1 comes from the fact that σ, σ + 1 are consecutive permutations and we need the first element in the permutation to swap out.
For your last point, just see that the relative ordering of the ai and bi ensures the inequality... the details are a bit messy so I'll spare you, but I think it's clear (try 35421 vs 41235, for example to see what happens).
Brilliant ideas!!
One question here, why you say contradicting the maximality of k? By the hypothesis of the induction, they are permutations of each other, however, this does not imply that ak + 1 = bk + 1 and so doesn't contradict.
Additionally, I think m doesn't have to be the maximal, it can be any value greater than longest common prefix.
Can someone explain how to check if the answer is on the left or the right?
UPD: I'm explaining the solution of Problem E...
In fact, the Theorem we used can be changed to:
For each
. So we only need to consider these two situations: point n+1 is in the set or not.
When you didn't realize the link in E was useful, so you had to come up with your own graph realization algorithm :(
Problem E is really not so friendly...
OMG! SO FAST!
Wish every coder : Happy New Year!
that was so fast , thank you for a great contest
Bitset works much better than FFT. https://codeforces.com/contest/1091/submission/47761694
That was fast insert Pikachu(o_o) meme
Here's a tutorial for similar optimizations as in problem H.
Alternate solution for B: Generate all points (xi + aj, yi + bj). Print the one that occurs n times.
Can you please elaborate it ??? I find it difficult to understand
since it proves that T always exists, so the equality (xi + aj, yi + bj) = T is always able to be satisfied?
so we compute all possible (xi + aj, yi + bj), since (xi + aj, yi + bj) = T is always able to be satisfied, and 1 ≤ i ≤ n,so this equality can be satisfied by (at least) n pairs of (i, j),so this solution is correct?
nah tbh i'm not sure as well :/
Thank You ! :)
But the time complexity is O(N^2log(N^2)), wouldn't that be a little too slow?
Not if n is 1000
T will be one of them (x_i + a_0 , y_i + b_0) (1<=i<=n)
so , iterate over them and check for n points code
Did the same but don't know why is it WA can you help please? 47738111
Wikipedia is useful for E but I didn't found it:(
I never saw this coming so fast :p
One can find complement of D (n·n! - an) in OEIS: A038156
god OEIS :/
I checked the sequence itself and also some intermediate results, but unfortunately not the complement.
If you had found the complement sequence, would you have put a different problem D?
Probably yes. And this problem would still be useful for a contest without Internet access, e.g. local ACM contest.
Damn i tried finding a$_n$ directly and couldn't find it. had to come up with a recurrence myself by just seeing patterns.
Me too... looks like I need to work on OEIS skills :/
Maybe you should work on your problem solving skills?
Haha, that goes without saying.
Why do we subtract from n.n! ?
How didn't my Recursive Backtracking get TLE on problem B? due to its elapsed time?
due to its elapsed time?
link here: http://codeforces.com/contest/1091/submission/47737516
I can't prove its time complexity but it seems to be like
Well seems it works much slower than
but it took only 0.5s ,how?
The Verdict is Accepted, isn't it?
so i'm confused :/
i thought it should get a TLE but it didn't
this makes me puzzled
Your solution's time complexity is about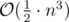 . In test 47 and 49, it equals 5 × 108.
. In test 47 and 49, it equals 5 × 108.
Thanks to Codeforces' amazing servers, it can pass the system test.
Wait, where did it say that sqrt in problem G returns a sqrt randomly?
You are choosing x randomly so in the n = pq case, the system doesn't know which of the four possible values of x yield a square of x2. The square root returned is random in the sense that it only depends on and not x.
and not x.
I can't understand C. Can Anyone explain?
it's easy to understand that, m = DivisorCountOf(n);
Now, how to get f_1, f_2 , f_3, ......f_m ?
What will be the series for some k , n (for all k , n%k == 0)
series len = n/k
so , series sum : len*(a_1 + a_len)/2
Here is the Code
how do you come to the point that for all the values of k such that n%k! =0, the resulted series will be a repeated form of some k for which n&k==0?
Why all k's are divisors of n
why k can't be 5 in above case
5 isn't a divisor of 6 (-_-)
Can anyone explain Problem C solution with example ?
Statement of problem B was very long and hard to understand hope to fix problems like that next time :)
Both My Solutions for B and C failed on main tests, but I can't seem to find my error.
Edit: I realized my Mistake with B
Problem B: https://codeforces.com/contest/1091/submission/47751047 Problem C: https://codeforces.com/contest/1091/submission/47762703
I think it is because your condition in selecting minimum and maximum point
if(a.x > max.x) { max = new Point(a.x, a.y); }
maybe the a.x = max.x but a.y > max.y you don't handle this condition in your code
the same thing in the min condition Java
Thanks, I forgot to consider that. Do you know what could possibly be wrong with my solution for C?
Can anyone explain the recurrence in D?
as far as i understood :
Well i thought about this while i was trying to solve as well it is true each part have same contribution , because when we switch the first digit ( 1 3 4 2 --> 2 1 3 4 ) the last digit of our last permutation is the same as the first digit of our next permutation during the switch , so concatenation of (1 3 4 2 + 2 1 3 4) , gives no sub string that has all 1 2 3 4. That's why they have equal contributions as the last digit will come twice always
I am not sure how they counted for a single part i had a different approach which is giving some answer right and some wrong..
but the recurrence is there as all the n! length string have same contribution , all starting with 1 , contribute the same as all starting with 2 , 3 and so on
d(n) = (d(n - 1) + (n - 1)! - 1) × n
Can anyone please explain D?
walnutwaldo20 told me that on D, if you split the sequence evenly into n consecutive parts (each part has length n!) then:
But we don't know why this is true. Does anyone know the proof?
edit: nvm ignore this
Well i thought about this while i was trying to solve as well it is true each part have same contribution , because when we switch the first digit ( 1 3 4 2 --> 2 1 3 4 ) the last digit of our last permutation is the same as the first digit of our next permutation during the switch , so concatenation of (1 3 4 2 + 2 1 3 4) , gives no sub string that has all 1 2 3 4. That's why they have equal contributions as the last digit will come twice always
Just explaining in case someone else also didn't understand this
I have used a similar approach and got ac. The sequences having first i(0<=i<=n-2) digits same will have equal contribution.here's my solution http://codeforces.com/contest/1091/submission/47756044 In my solution I have added n! initially and looped from 1 to n-2 which is same as looping from 0 to n-2.
thanks
The constraints on problem E seem incredibly tight.
Many
O(N * log^2(N))didn't pass (which is unsurprising, given 500K elements and 2 seconds). I thought the limit was so tight especially so that such solutions wouldn't pass (since there is a linearithmic solution), but the editorial does mention aO(N * log^2(N))solution, so it seems like it was intended to pass after all?.3 10 10 50 WGL
In problem F how is the ans 220 for this ? I think it should be 240? Am i missing something? pls help
Swimming for 120 minutes, gaining 40 stamina, then 50 minutes for grass getting another 10 stamina and 50 minutes for lava. 120 + 50 + 50 = 220min
Example of my pattern
I need help with why my solution is wrong for D So basicly my approach is dividing it into 2 parts , 1 is the obvious n! arrangements of 1 to n , then concatenations of 1 to 2nd and 2nd to 3rd and so on So what i found out was , when we check from 1st to 2nd we get exactly n-2 , from 2nd to 3rd we get n-3 this alternates all the way till the first digit is changed i.e ( 1 4 3 2 — > 2 1 3 4) so as each different digit startings ( 1 2 3 4 .... , 2 1 3 4 ... ) contribute the same amount so i found out the result for 1 2 3 4 and multiplied it by n for patterns starting with 1 , i did ((n-1)!)/2 * (n-2) + (((n-1)!/2) -1)* (n-3) , the -1 in 2nd case because last transition for digit change would have no substring that has all 1 to n Can anyone help me out
http://codeforces.com/contest/1091/submission/47759220
its giving correct answer for some cases and for some it is giving a wrong answer
Can I get a better explanation of D?
Here's how I did it
Two ways to have the required subarrays:
Now,
front * back ∀ i + n! will be the answer143534711I have solved 'D' by finding patterns.
Divided into some points:
(Ex-1: n=3, 1234 & 1243; 2nd place from right or 3rd from left. Ex-2 : n=3, 1243 & 1324; 3rd place from right or 2nd from left.)
Here comes my pattern finding. For 2nd place(from right) ELSA is n-2, for 3rd place(from right) ELSA is n-3, for 4th place(from right) ELSA is n-4, goes on unless ELSA is 1 at the (n-1)-th place.
Now I have to find how many adjacent pairs of permutation have X-th digit(from right) variant.
Finding amount of each X-th digit variant: (By example, for n = 4): 1. 1-th variant or, number of permutation : 4 * 3 * 2 * 1 = 24 2. 2-th variant : 4 * 3 * (2-1) * 1 = 4 * 3 * 1 * 1 = 12 (ELSA = 2) 3. 3-th variant : 4 * (3-1) * 1 * 1 = 4 * 2 * 1 * 1 = 8 (ELSA = 1) 4. 4-th variant or n-variant never need because it's corresponding ELSA = 0. Now, 24 + (12*2) + (8*1) = 56.
Thank you so much ! :)
Can you please further explain how to find the X-th digit(from right) variant? And one more thing i want to clarify, ELSA's of 1-th variant (from right) = no. of permutations i.e. n! Thanks in advance:)
Finding amount of each X-th digit variant: (By example, for n = 4):
Now, 24 + (12*2) + (8*1) = 56.
I just decrement X-th place number(from right) for each X-variant. I did this to find how many pairs of permutation are there, where they create X-th variant. If you think in a permutational way, you will find that this is a correct way to calculate those pairs.
Check My Implementation: https://codeforces.com/contest/1091/submission/47767219
Your method is perfect! Thank you very much :)
Problem E can also be solved without using the property that the answer lies in a contiguous interval (yeah, guess who didn't realize this during the competition).
Following the Erdos-Gallai theorem, assume we want to check whether d could be the answer. Let p be the position d would be in the degree array. For every position i ≤ p, d would appear on the left hand side of the inequality, thus posing a lower bound on d; for every position i > p, d would appear on the right hand side, thus posing an upper bound.
The bounds at each position can be preprocessed using prefix sums (for right hand side we could do a binary search instead of value counts), and we can also perform another scan to obtain the "prefix lower bounds" and "suffix upper bounds" (i.e. intersection of prefix/suffix bounds). To check whether d could be the answer, just check the prefix and suffix bounds, and also whether the inequality satisfies at position p itself. Checking one value takes time (just have to do a binary search), so the whole algorithm is
time (just have to do a binary search), so the whole algorithm is  .
.
One caveat that can be ignored: we still need to take the min function on the right hand side into account: if i < d then we should ignore the bound. This means that when checking the answer, instead of using the "prefix" bound, we should use the bound of an interval, which is the maximum value in the interval. This is an static RMQ problem and can be solved in O(1) using sparse tables. However, it seems that the lower bounds are non-decreasing (bounds at higher indices are always tighter (larger)), so this is unnecessary.
In the contest I solved it only realizing it had to be a contiguous interval between [ai, ai + 1] where the ai's are the integers in the input in sorted order.
Well, I just want to mention that this solution can be hard to implement. During the contest I also came up with a similar idea, but it took me more than 1 hour to code.
Yes, you're right. I had a bunch of off-by-one errors before I could get it to work.
Indeed, it's quite a bother to implement. The version I got in the contest is actually O(n) after sorting: 47753124. The prec0 and prec1 arrays correspond to the "sum of mins" part in the formula which can be precomputed by two pointers, and the lower/upper bounds are accumulated once and for all in opposite directions.
How do you mean its O(logN) per value? For every value, you need to check all preffixes, not only one, isnt it O(n) per value? Looks like you are checking only prefix till new value but that does not make sense, becase that is not only prefix that can make inequality wrong.
To check whether degree d could be an answer, we need to first find the position p of d in the sorted array of degrees. Then, we need to check whether all n inequalities hold. These can be categorized by their positions i into three types: i < p, i > p, and i = p. As I mentioned in the previous post, each type could be checked within time with a bit of preprocessing. It's a bit hard to explain so I won't go into details here, feel free to check out my submission: 47769662.
time with a bit of preprocessing. It's a bit hard to explain so I won't go into details here, feel free to check out my submission: 47769662.
I am still a Beginner ^ _ ^ need help in A please
iterate from 100 to 1 for finding valid number of flower code:: scanf("%d %d %d",&a,&b,&c); for(int i=105;i>=0;i--) { if(i<=a+1&&i<=b&&i+1<=c){ cout<<3*i;break; } }
Let me share my approach on D!
We can observe (I have yet to figure out how!) that valid subarrays are the ones that contain all the n distinct numbers (from 1 to n). So, for example, for n = 5: [4, 2, 3, 5, 1] is a valid one, but [4, 2, 2, 3, 1] is not!
So, now let's write down the concatenation of the permutation for n = 4 (hoping to find a useful pattern):
1 2 3 4 (p1)
1 2 4 3 (p2)
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
.... (pn!)
Obviously, for each p, all the subarrays that start at the beginning are valid (n! so far). (S0 = n!)
What about the the ones that are beginning at the middle of p? (for example, on p1, the [2, 3, 4, 1] subarray?)
As you can see, we need the part of the subarray that belongs to the next p (its prefix) must be equal to the prefix of the current p. So, for instance, on p1 if we take (again) the [2, 3, 4, 1] subarray, we observe that the part which overlaps with p2 (ie. the 1) occurs on p_1, too! So, by applying this reasoning, we can conlude the following:
If the subarray begins from 2nd number of a p (it ends on the 1st number of the next p), it is invalid only when the 1st number is changed (see the last p on the example) (ie when 1st number on permutation become 1 (the first number), 2, 3, 4, ..., n). The valid subarrays for this case are S1 = n! (total permutations) — n
If the subarray ends on the 2nd number of the next p, it is invalid only when the 2nd number changes (ie. when the prefix becomes _ -> [1, 1], [1, 1] -> [1, 2], ..., [1, 4], [2, 1]) and this happens n * (n — 1) times, so S2 = n! — n * (n — 1)
...
By continuing like this, we get Sk = n! - n·(n - 1)·...·(n - k + 1)
Hence, we need to calculate the following expression:
ans = S0 + S1 + ... + Sn = n! + (n! - n) + (n! - n·(n - 1)) + ... + (n! - n!) = n·n! - (n + n·(n - 1) + ...)
How can we calculate the second part?
We can use DP, where:
DP[n] = n
DP[n - 1] = DP[n]·(n - 1)
...
DP[k] = DP[k + 1]·k (until k = 2 is enough)
And we sum them! :)
I hope that this helps!
you don't need to calculate the second part using dp. just sum it is ok.
Oh really! How?
http://codeforces.com/contest/1091/submission/47776405
After reading so many solutions, only yours I understand, you deserve more likes, here I give you a belated like :)
CAN you explain what do you mean by this ---->
If the subarray begins from 2nd number of a p (it ends on the 1st number of the next p), it is invalid only when the 1st number is changed (see the last p on the example) (ie when 1st number on permutation become 1 (the first number), 2, 3, 4, ..., n). The valid subarrays for this case are S1 = n! (total permutations) — n
For problem E: I found the Erdős–Gallai theorem after googling with something like "valid degree sequence". After some investigation into the theorem, I figured out that a solution could be devised using it. However, there are so many details (at least for me) involved in the adaption of the theorem to this problem that I couldn't make it within the last one and a half hour during the contest :(. For those who may be interested in this approach, see my submission 47772075 for detail. The complexity is .
.
How does one show that the given solution for F is optimal?
I just thought the link was to explain the statement during the contest...
Cannot imagine there exist some solutions...
In the problem E,how to make Havel–Hakimi algorithm faster?
calculate the prefix sum of di at first so you can calculate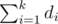 in O(1)
in O(1)
enumerate k from n to 1,define cnti as the amount of dj(k ≤ j ≤ n) which equals to i,then you can calculate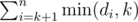 in O(1)
in O(1)
(every time k is decreased,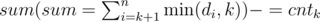 ,and for dk,add it to sum and cntdk if dk ≤ k)
,and for dk,add it to sum and cntdk if dk ≤ k)
then you can do it in O(n)
Thank you.But what your said is Erdős–Gallai theorem.In the soluton above,majk mentioned that "Alternatively, we can perform a similar binary search using Havel-Hakimi algorithm, using a segment tree or a multiset and tracking whether the an + 1 was already processed or not to find out whether the answer is too small or too big. This yields O(nlog2n) algorithm." .But I don't know the detail about it.
emmm... I don't know how to use a segment tree or a mulitset to make it faster,but I know how to use splay to do it.
In Havel–Hakimi algorithm,you need to find the maximum ,delete it and decrease the biggest k numbers.
take di as the key value,the first and second operation will be simple.
for the third operator,splay the (k+1)th number to root(if the kth and (k+1)th are equal and on the same node,split the node),mark on the root's left son,delete the root and insert it back(after decreasing the biggest k numbers,the root might be less than its left son(assume we put the bigger node on the left),so we reinsert it to make it in the right place).
note that the third operation is very complex.
That's right ! Thanks a lot ! Happy new year!
Problem E is terrible for someone who didn't care about the link.
It's really surprising that part of the solution is offered in the description.
I passed H without bitset.
Maintain a list of vectors, vector[i] contains all j's which grundy[j] = i. When calculating grundy[x], find y from vector[0], vector[1], ... orderly. While finding in vector[i], if x-y is available, break, and if no break happens in vector[j], then grundy[x] = i and finish.
I can't prove the time complexity, but it performs well.
Alternatively, we can perform a similar binary search using Havel-Hakimi algorithm, using a segment tree or a multiset and tracking whether the an+1 was already processed or not to find out whether the answer is too small or too big. This yields O(nlog^2 n) algorithm. So,can a solution Accepted this problem with O(n log^2 n)?n=500000 and n log ^2n=1.8e8.Also multiset is very slow.... P.S. 5e5 is enough to make python programmer TLE in input.
It's said that the time limits are based on Java...
In Java,5e5 is enough for TLE,I think
Shouldn't the sum in the explanation of D should be instead of
instead of 
Fixed, thanks.
I cannot figure out how to make the Havel-Hakimi algorithm faster. How can I sort the degree sequences after each update operation if I use segment tree?
If we do not work out the factor list first, but use the following code
if n mod k = 0 then continue, can it pass the tests in problem C?Can someone explain why maximum Grundy number on H is 100? I was hoping the editorial would explain it but it didn't.
I made some videos with more detailed explanations for some of the problems. I think my solution to F is a bit simpler than the editorial; the idea is to start with flying over everything and proceed greedily from there.
A: https://www.youtube.com/watch?v=Ue7gAIwhSoo
B: https://www.youtube.com/watch?v=sY1WOkz8K28
C: https://www.youtube.com/watch?v=CFP_lctIss4
F: https://www.youtube.com/watch?v=oj6bcK405lc
How to do binary search over a boolean array as said in editorial for E? Array is something like [ N, N, N, Y, Y, Y, N, N]. Plz suggest a general approach.
I know how to binary search range in sorted sequence but this sequence does not appear to be sorted.
Once you determine that the answer is no, you can figure out if you are too high or too low based on where you fail. For example, for the degree sequence [4 3 2 1 ?], if we try setting ? as 3, and then do erdos gallai, the first 2 inequalities work (4<=0+4) & (4+3<=2 +(2+2+1)), but the third does not (4+3+3>6+(2+1)). Now, looking at just this inequality, the edge with length 3 increases the left side, but not the right. So increasing 3 will not work, and we know the answer is hence less than 3.
If we try to make the answer 1, then the second inequality won't be satisfied, as 7>2+(2+1+1). If we decrease the answer further, the inequality still won't be satisfied, since it will be decreasing the right side of the inequality only (instead we will have 7>2+(2+1+0)). So the answer is greater than 1. Hence we only have to check 2 and that works.
Auto comment: topic has been updated by majk (previous revision, new revision, compare).
For those don't know Lexicographically Next Permutation algorithm.
Algorithm link
Problem D: I read the tutorial and i interpret that we are trying to find the answer by subtracting all the false subarrays.
For each permutation seperately , n! should be added to answer
And for second part in the tutorial They are taking number of total subarrays as n.n! . I can't understand this Can anybody please further explain this? Thanks in advance:)
In question E , i think testcases are not so strong. Because in following testcase , solution of ecnerwala fails. That testcase is :
9
4 3 2 2 2 2 1 0 0
Actual answer should be [0,2,4,6] , but according to his solution , output is [0,2,4,6,8] . Link to his solution is https://codeforces.com/contest/1091/submission/47743506 .
Oops, looks like you're right, I had an off-by-one that wasn't caught. It's fixed here 47800829 if anyone cares.
How to prove the greedy solution for F? In editorial there is an algorithm and reasons for it, but I still dont understand how to prove such solutions, when one changes previous steps of the strategy.
First, you need to fly to pass lava. Then we greedily choose to gain as much stamina as we can. So we walk on grass and swim in water. There are two situations. 1. If we still run out of stamina at some place. Then we need to do some extra work to gain stamina. So we need to go backward and forward at some place before. 2. If through this method we can spare some stamina in the end, then in fact we can spend them before. The solution discuss this situation detailedly.
In problem C : Can someone explain What is the intuition or proof behind using only divisors as K values which give unique sums?
for each k , series : 1 , 1+k , 1+2k , 1+3k , ...... , 1 + x*k ;
where , (1 + x*k)%n == 1
so , (x*k)%n == 0
convince yourself , that (x*k) == n , not 2n,3n,4n.....
that means k is a divisor of n
why did you rejected 2n,3n,4n... ??
Think the circle as 0,1,2,...n-1. You wanna back to 0 not 1.
Now series : k,2k,3k,....,x*k
you stop tour after finding first x such that (x*k)%n == 0 ;
Now, you tell me how a number forms with it divisors? say 12 ::
3 , 2*3 , 3*3 , 4*3 (which is 12 itself)
The fun value only depends on gcd(k,n), so you only need to iterate over possible gcds, and all gcds divide n (that's part of the definition of gcd!)
In D, Why do we subtract from n*n!?
There are n! permutations , from each of them we can get at most n segments (1 from it , n-1 from its_suffix + next's_prefix) with sum of segment == n*(n+1)/2
For our last permutation we don't have
( suffix_i + prefix_(i+1) == n*(n+1)/2 )
so why we counting n from the last one?
Look , last one has bad suffixes of length 1,2,3...n-1 ; All of which are includes in subtraction process ...-
Hey , I'm a newbie and just beginning CP. In Problem C , why the formula ,N*(i-1)/2 + i and N*(N/i-1)/2 + N/i , Can someone please explain this formula ? And it's significance in the problem ? What is the need for this formula , why not basic AP sum where d=i ? How do people crack such formula's within 2:30 hrs ?
The numbers that are hit are 1 d+1 2d+1 ... n+1 (=1). If you sum the arithmetic sequence you get the formula mentioned. Wolfram Alpha can do these kinds of sums for you: https://www.wolframalpha.com/input/?i=sum+1%2Bd*k+for+k%3D0+to+n%2Fd-1 (not sure if this is the exact right one).
I made a video explaining the solution in more detail that may help: https://www.youtube.com/watch?v=CFP_lctIss4
Can't understand why i need to consider only k that divides n. Can anyone explain that moment in other words than in editorial pls?
The fun value only depends on gcd(k,n), so you only need to iterate over possible gcds, and all gcds divide n (that's part of the definition of gcd!)
Problem E:How can you prove that "on the integers of same parity, the answer always forms a continuous interval"
I do not have a simple mathematical proof, but you can definitely see this fact from the statement of Erdos-Gallai.
We assume that x is the smallest possible answer for an + 1, assuming that there is an edge u - v in the graph, then we can change this edge to u - k, k - v without changing the degree of other points, obviously we have found that the degree of k has increased by 2, and this can be done for all other edges, so the possible answer for x is continuous and has the same parity.
You also have assumed that neither of u-k and v-k was already formed
In problem G:
Shouldn't it be ?
?
I think so. This is a typo.
毒瘤啊
define TOO_HUGE lyz
Problem H:How can you proof that the Grundy number is less than 100?
"Coming back to our problem, if the suffix of length k is in decreasing order, than the prefix of length n−k of the next permutation has different sum from the prefix of the same length of the current permutation, hence the subarray has incorrect sum."
This statement requires a proof: a slick inequality statement which proves this. :D
In editorial of problem D, why we subtract from n*n! ? Is the given formula in simplified form? I can think of the number of subarray of length n is n*n!-n+1
Because when we are doing the sum, the last permutation is in the formula $$$\sum_{k=1}^{n-1}$$$(n!/k!). In other words, you can solve it by the formula (n*n!-n+1 — $$$\sum_{k=1}^{n-1}$$$(n!/k!-1)). Subtracting 1 from n!/k! means that we are not going to take the last permutation into account.
can you please explain from where this formula came
n!/k!and i am not getting if we choose the firstn-kelements freely as given in the tutorial we may be calculating the suffices repeating(means more than once) how are we so sure...please once more elaborate for meAs the editorial said we are permuting the first
N - Kelements freely. This means for the first N-K indices we havenP(n-k)which is nothing butN! / (N - (N - K)!->N! / K!I wonder if there is a convincible proof for the Grundy number of problem H is less than 100 or the problem setter just used programs to find it out