Given a grid of size 3 x n (n <= 10^5), consists of empty cells (marked with dot '.'), occupied cells (marked with sharp '#'), asterisks (marked with '*'), and many character 'S' and 'T'. A path connecting S and T is good if the following conditions hold:
It doesn't pass through any other S and T.
It doesn't pass through occupied cell ('#')
It passes through at most 1 asterisk.
Moreover, paths are not allowed to intersect each other. From a cell you can only go to a cell sharing an edge to current cell. Calculate the maximum number of path in the grid.
I haven't got any idea for this problem. Thank you and appreciate for any help.










Maximum flow solution:
Imagine that you want the path to not pass the asterisks at all. The actual probelm can be solved by the same construction but on two layers.
Create 2 vertices for each cell of the table and add a direct connection from the first ("in" vertex) to the second ("out" vertex) with capacity 1. The general idea is to add the adjacent connections by creating direct edges from the "out" parts to the "in" parts. These connections will have capacity 1 too. Finally we link the source to all S vertices and all T vertices to the sink. These connections should have capacity 1 again. If we apply Dinic, the complexity will be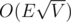 , as we have a unit capacity graph.
, as we have a unit capacity graph.
To solve the original problem, we will have two layers — the connections are the same and the only difference is that when we have an adjacent asterisk cell, we change the layer and go to the second one. The second layer has no connections to adjacent asterisk cells. Also we should be careful to add connections to S vertices only on the first layer.
Another note is that when we add the direct connections we shouldn't add such connections that they go to a S cell.
Thank you, I was stuck in how to handle one asterisk condition in flow network
How would you handle not going through the same cell twice (in the different layers)?
So if you find an augmenting path going through first layer to the second, how do you make sure that no other path can use the cells used in the first layer again in the second layer — and vice versa?
You are right. I don't see an easy way to fix the solution, but we can do a solution in O(N * 23 * 23) with the following DP: dp[column][mask of rows that have a S path started][mask of rows that have a T row started]. Probably you can figure out the transitions (you should merge the S and T paths).