Hello, Codeforces! The reason why I am writing this blog is that my ACM/ICPC teammate calabash_boy is learning this technique recently(he is a master in string algorithms,btw), and he wanted me to provide some useful resources on this topic. I found that although many claim that they do know this topic well, problems concerning inclusion-exclusion principle are sometimes quite tricky and not that easy to deal with. Also, after some few investigations, the so-called "Inclusion-Exclusion principle" some people claim that they know wasn't the generalized one, and has little use when solving problems. So, what I am going to pose here, is somewhat the "Generalized Inclusion-Exclusion Principle". Most of the describing text are from the graduate text book Graduate Text in Mathematics 238, A Course in Enumeration, and the problems are those that I encountered in real problem set, so if possible, I'll add a link to the real problem so that you can solve it by yourself. I'll start with the basic formula, one can choose to skip some of the text depending on your grasp with the topic.
Consider a finite set 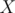 and three subsets
and three subsets 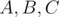 , To obtain
, To obtain 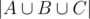 , we take the sum
, we take the sum 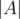 +
+ 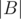 +
+ 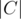 . Unless
. Unless 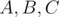 are pairwise disjoint, we have an overcount, since the elements of
are pairwise disjoint, we have an overcount, since the elements of  has been counted twice. So we subtract
has been counted twice. So we subtract  . Now the count is correct except for the elements in
. Now the count is correct except for the elements in 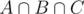 which have been added three times, but also subtracted three times. The answer is therefore
which have been added three times, but also subtracted three times. The answer is therefore
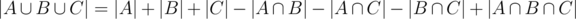
, or equivalently,
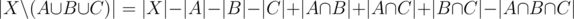
The following formula addresses the case applied to more sets.
The Restricted Inclusion-Exclusion Principle. Let 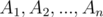 be subsets of
be subsets of 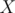 . Then
. Then
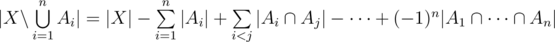
This is a formula which looks familiar to many people, I'll call it The Restricted Inclusion-Exclusion Principle, it can convert the problem of calculating the size of the union of some sets into calculating the size of the intersection of some sets. It's not hard to prove the correctness of this formula, we can just check how often an element 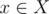 is counted in both sides. If
is counted in both sides. If 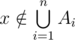 , then it's counted once on either side. Suppose
, then it's counted once on either side. Suppose  , and more precisely, that
, and more precisely, that  is in exactly
is in exactly 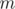 of the sets
of the sets 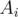 . The count on the left-hand side is
. The count on the left-hand side is  , and on the right hand side, we have
, and on the right hand side, we have
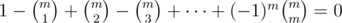
for 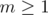 , thus the equality holds.
, thus the equality holds.
Example 1. Let's see an example problem Co-prime where this principle could be applied: Given 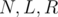 , you need to compute the number of integers
, you need to compute the number of integers  in the interval
in the interval 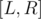 such that
such that  is coprime with
is coprime with 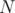 , that is,
, that is, 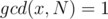 . There are
. There are  testcases. Constraints:
testcases. Constraints: 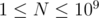 ,
,  .
.
The standard interpretation leads to the principle of inclusion-exclusion. Suppose we are given a set 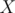 , called the universe, and a set
, called the universe, and a set 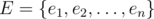 of properties that the elements of
of properties that the elements of 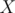 may or may not process. Here we can define the properties as we like, such as
may or may not process. Here we can define the properties as we like, such as 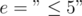 ,
, 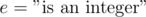 , or even
, or even 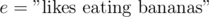 . Let
. Let 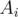 be the subset of elements that enjoy property
be the subset of elements that enjoy property 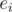 (and possibly others). Then
(and possibly others). Then 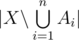 is the number of elements that process none of the properties. Clearly,
is the number of elements that process none of the properties. Clearly, 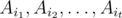 is the set of elements that possess the properties
is the set of elements that possess the properties  (and maybe others). Using the notation
(and maybe others). Using the notation
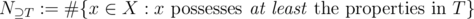

we arrive at the inclusion-exclusion principle.
Inclusion-Exclusion Principle. Let 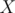 be a set, and
be a set, and 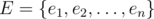 a set of properties. Then
a set of properties. Then
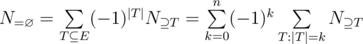
The formula becomes even simpler when 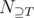 depends only on the size
depends only on the size 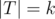 . We can then write
. We can then write 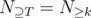 for
for 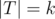 , and call
, and call 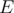 a homogeneous set of properties, and in this case
a homogeneous set of properties, and in this case  also depends only on the cardinality of
also depends only on the cardinality of 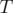 . Hence for homogeneous properties, we have
. Hence for homogeneous properties, we have
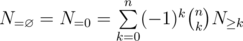
This is the very essence of Inclusion-Exclusion Principle . Please make sure you understand every notation before you proceed. One can figure out, by letting  , we arrive at the restricted inclusion-exclusion principle.
, we arrive at the restricted inclusion-exclusion principle.
Example 2. This problem Character Encoding requires you to compute the number of solutions to the equation  , satisfying that
, satisfying that 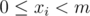 , modulo
, modulo 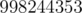 . Constraints:
. Constraints: 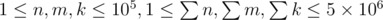 . Hint: the number of non-negative integer solutions to
. Hint: the number of non-negative integer solutions to  is given by
is given by  .
.
Example 3. Well, this one is a well-known problem. K-Inversion Permutations. The statement is neat and simple. Given N, K, you need to output the number of permutations of length N with K inversions, taken modulo  . Constraint:
. Constraint:  .
.
Example 4. This problem comes from XVIII Open Cup named after E.V. Pankratiev. Grand Prix of Gomel.Problem K,(Yes, created by tourist:) ) which gives a integer 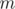 , and requires one to find out the number of non-empty sets of positive integers, such that their greatest common divisor is
, and requires one to find out the number of non-empty sets of positive integers, such that their greatest common divisor is  , and their least common multiple is
, and their least common multiple is 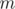 , taken modulo
, taken modulo 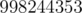 .Constraint:
.Constraint: 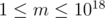 .
.
I guess that's the end of this tutorial. IMO, understanding all the solutions to the example problems above is fairly enough to solve most of the problems that require the inclusion-exclusion principle(but only for the IEP part XD). This is my first time of writing an tutorial. Please feel free to ask any questions in the comments below or point out any mistakes in the blog.



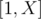 such that
such that 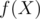 , then the answer is
, then the answer is 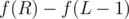 . How we're gonna compute
. How we're gonna compute 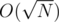 and then find all prime factors
and then find all prime factors 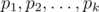 of
of 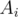 be the set of numbers that are divisible by
be the set of numbers that are divisible by 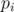 , then the answer is the
, then the answer is the  , which may be hard to compute directly. However, using the restricted inclusion-exclusion principle, we can convert the problem into computing the size of the intersection of sets, which is trivial. Time complexity is
, which may be hard to compute directly. However, using the restricted inclusion-exclusion principle, we can convert the problem into computing the size of the intersection of sets, which is trivial. Time complexity is 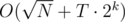 , with
, with 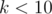 equals to the number of distinct prime factors of
equals to the number of distinct prime factors of  . To do that, we apply the inclusion-exclusion principle. Let
. To do that, we apply the inclusion-exclusion principle. Let 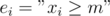 , then
, then 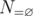 is our desired answer. Clearly, this set of properties is homogeneous. Take
is our desired answer. Clearly, this set of properties is homogeneous. Take  , then
, then 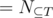 is the number of solutions with
is the number of solutions with 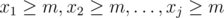 . Setting
. Setting 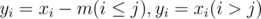 , and it's the same as the number of solutions of the system
, and it's the same as the number of solutions of the system 
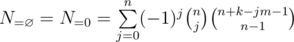
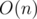 , due to precomputing factorials and the modular inverses of factorials.
, due to precomputing factorials and the modular inverses of factorials.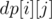 as the number of permutations of length
as the number of permutations of length  with
with  inversions. The recurrence is also trivial:
inversions. The recurrence is also trivial:  . This is
. This is 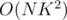 , and can be optimized to
, and can be optimized to 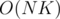 using prefix sums, which is still not enough due to the given constraints.
using prefix sums, which is still not enough due to the given constraints. to the number of inversions, so the answer is equal to the number of solutions to
to the number of inversions, so the answer is equal to the number of solutions to  .
.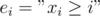 , then
, then  , then the number of solutions to the equation is
, then the number of solutions to the equation is 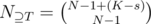 . Therefore, we can group those sets together. By inclusion-exclusion principle,
. Therefore, we can group those sets together. By inclusion-exclusion principle, 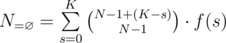
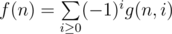
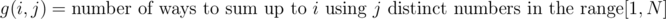 .
.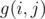 . We can use the technique as we can computing partition numbers. Partition
. We can use the technique as we can computing partition numbers. Partition 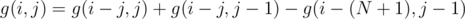 . Another important observation is that there are at most
. Another important observation is that there are at most 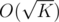 valid values for
valid values for  .
. , and then what remains, is a prime
, and then what remains, is a prime 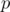 , a square of a prime
, a square of a prime 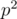 , or a product of two distinct primes
, or a product of two distinct primes 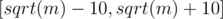 to check if it's the second case, and otherwise the last case.
to check if it's the second case, and otherwise the last case.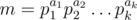 . We need to avoid counting the cases with
. We need to avoid counting the cases with 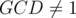 and
and 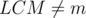 , thus we should apply inclusion-exclusion principle. Let
, thus we should apply inclusion-exclusion principle. Let 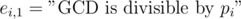 and
and 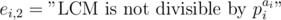 . Then the answer is
. Then the answer is 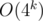 ,which is too much for
,which is too much for 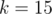 in te worst case. However, noticing that two of the options of for each prime divisor lead to same computations, the complexity can be reduced to
in te worst case. However, noticing that two of the options of for each prime divisor lead to same computations, the complexity can be reduced to 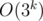 .
.






Auto comment: topic has been updated by Roundgod (previous revision, new revision, compare).
I think in the formula of example 3, it should be f(s) instead of f(i). Furthermore, can you explain how did you calculate f(n)?
Fixed, thank you! Since each possible combination of j distinct numbers in the range [1, N] that sum to n contributes to f(n) according to the inclusion-exclusion princple, and the inclusion-exclusion coefficient(that is, the ( - 1)i term) is determined by the parity of j. So if we can find out the number of ways to choose j distinct numbers in the range [1, N] that sum to n, which is g(n, j), efficiently, then we can then calculate f(n).
Thanks, got it.
Can Someone Please tell me how to solve this Problem. I think it can also be done using inclusion exclusion but dont know how.
UPD: Image of the problem: link
I don't think it can be solved using inclusion-exclusion. You can use digit dp to solve it. Here's my solution.
Add this problem also https://atcoder.jp/contests/abc152/tasks/abc152_f
This is really a nice tutorial, liked it. Hope to get more nice tutorials like this in future.
In the formula for f(n), the condition should be i>=0, so that f(0) = 1.
Also, the formula for g(i,j) is incomplete. For i = 12, j = 3, N = 5, it gives answer 3, whereas correct answer is 1 i.e, {{3, 4, 5}}.
Oops. I wrote it wrong. It should be $$$g(i,j)=g(i-j,j)+g(i-1,j-1)$$$. Now fixed, thank you!
Sorry, but the formula still gives wrong answer for the example I mentioned.
According to the updated formula for N = 5, $$$ g(12, 3) = g(9, 3) + g(11, 2)$$$.
Now, $$$g(9, 3) = 2 $$$ i.e, {{1,3,5},{2,3,4}} and $$$g(11, 2) = 0$$$ i.e, {}, which implies $$$ g(12, 3) = 2 + 0 = 2$$$.
This is wrong as the only way to do this is {3,4,5}, so $$$g(12,3)=1$$$.
Also, would you please explain how are you getting the formula?
Oh, I forgot the constraint of $$$N$$$. So basically what I wanted to represent is to split the cases into two: whether there is a one in the set of numbers, that is, $$$g(i,j)=g(i-j,j)+g(i-1,j-1)$$$, but we may have an $$$N$$$ present in the set of $$$g(i-j,j)$$$, which is forbidden. Thus the final formula should be $$$g(i,j)=g(i-j,j)+g(i-1,j-1)-g(i-j-N,j-1)$$$. Thanks for pointing out!
UPD: for getting the formula, we check if there is an one in the set, if there is, we erase it, otherwise we let all numbers in the set minus one, which is basically the recurrence one may reach when calculating some partition numbers.
Thanks for clearing things up. Waiting for part 2.
Can't it now happen that $$$1$$$ is already part of $$$g(i-1,j-1)$$$?
I.e. shouldn't the formula instead be more like $$$g(i,j) = g(i-j,j) - g(i-j-N,j-1) + g(i-j,j-1) - g(i-j-N,j-2)$$$? But aren't we then in turn running the risk of subtracting sets with $$$N$$$ too many times as $$$g(i-j-N,j-1)$$$ already may contain $$$N$$$?
(Thumbs up on a great blog post btw.)
Ahh...My bad. Another(hope also is the last) edit: for this problem, we may use another way of constructing sets, we check if there is an one in the set, if there isn't, we let all numbers in the set minus one, otherwise we erase the one, and then let all remaining numbers in the set minus one. Also we need to subtract the case where the biggest number was $$$n$$$ in the reduced set.
Let's restate the formula: $$$g(i,j)=g(i-j,j)+g(i-j,j-1)-g(i-(n+1),j-1)$$$
i dont understand the difference between this formula for $$$g(i,j)=g(i−j,j)+g(i−j,j−1)−g(i−j−N,j−1)$$$ and the formula given in updated editorial , why is this not right, i feel this is right.
Recall that $$$g(i,j)$$$ is the number of ways to sum up to $$$i$$$ using $$$j$$$ distinct numbers in the range $$$[1,N]$$$, when subtracting $$$1$$$ from all elements, we actually changed the range to $$$[1,N-1]$$$, and that's the part we've overcounted, we've additionally counted sets with maximum $$$N$$$ in the part where we've subtracted $$$1$$$ from all numbers, which corresponds to sets with maximum $$$N+1$$$ in the original part, so we need to subtract the number of sets with maximum $$$N+1$$$ in the original part, which is $$$g(i-(N+1),j-1)$$$. Therefore we have the formula in the tutorial. Note that this overcounting happens for both cases when we discuss if there is a one in the set, and the formula you give only takes care of one of the cases.
Thank you, Roundgod, for such a wonderful explanation.
Auto comment: topic has been updated by Roundgod (previous revision, new revision, compare).
Sorry for asking these silly questions but what knowledge or definitions I need to learn in order to understand what is $$$N_{\supseteq T}$$$, $$$N_{= T}$$$, $$$N_{= \emptyset}$$$, ... and what really $$$N$$$ and $$$T$$$ represents for in this definition: (Because it just pops up from nowhere and I could not understand).
Thanks for reading and helping me!!.
i have query related to generalisation of example 3. x1+x2+x3.....xn=k and xi< rand(1,n) . can it be solved using inclusion exclusion.
I am interested in example 3, can I optimize furthur, about ($$$O(m \times polylog(m))$$$ time complexity) ?
I don't understand the part from "The formula becomes even simpler when ...", specifically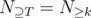 and what does homogeneous mean ?
and what does homogeneous mean ?
There is a straightforward $$$O((N+K)logK)$$$ solution (but with bad constant factor) to the 3rd problem K-inversion Permutations using generating functions and Fast Fourier Transform.
Required answer is the coefficient of $$$x^K$$$ in the polynomial $$$P(x) = (1) * (1 + x) * (1 + x + x^2) * ... * (1 + x + ... + x^{(N-1)})$$$
It can be rewritten as $$$P(x) = \prod _{i=1}^N \dfrac{1 - x ^ i}{1 - x}$$$
It is tough to calculate this polynomial, but easy to calculate the log of this, which will be:
$$$Q(x) = logP(x) = (\sum _{i=1}^N log(1 - x ^ i)) - N \cdot log(1 - x)$$$
We know that: $$$log(1-x^i) = -\sum _{j = 1} ^\infty \dfrac{x^{i \cdot j}}{j}$$$. We only need to calculate this uptill $$$x^K$$$. It can be done naively in $$$O((N+K)logK)$$$
Now all we need is the coefficient of $$$x^K$$$ in $$$e^{Q(x)}$$$. This can be done using FFT in $$$O(KlogK)$$$. It is a bit complicated but it is described here — https://cp-algorithms.com/algebra/polynomial.html
Wow, amazing! How did you think of that generating function? If I am not wrong, you are choosing, for every index i, how many elements to the left of ith index are bigger than the element at the ith index. And these things, together will determine the permutation, somehow... Wow!
The product of (1 — x^i) has a simple formula using the pentagonal number theorem.
Oh i didn't know that there's a direct formula for that.
Btw, after that, we also need to divide by (1-x)^N, all i can think right now is binary exponentiation and inverse series, but that will be log^2. Is there a faster approach for this, that i'm missing?
We can compute the binomial expansion of $$$(1 - x)^{-N}$$$ in linear time and convolve.
oh yes, my bad, thanks.
Sorry if this is a dumb question, but how would we use this result in this task? For $$$K > N$$$, we can't just take the first $$$(K + 1)$$$ terms of the pentagonal expansion to compute $$$\prod_{i=1}^N (1 - x^i)$$$ up to $$$x^K$$$ — is there a way to get rid of the contribution of factors that are present in the infinite product but not in the finite one?
You're right. I didn't notice that K could be greater than N.
I understood this finally; maybe I understood the relation better with examples.
Lets take example : calculate $$$g(20 , 3)$$$ N = 9 ,range = [1,9]
- Our possibilities:
- 3 + 8 + 9
- 4 + 7 + 9
- 5 + 6 + 9
- 5 + 7 + 8
According to relation $$$g(i,j) = g(i-j,j)+g(i-j,j-1)-g(i-(N+1),j-1)$$$
$$$g(i-j,j)$$$ : number 1 is not included in the set. Subtract one from all numbers.
Here $$$g(i-j , j)$$$ corresponds to $$$g(17 , 3)$$$
$$$g(i-j,j-1)$$$ : number 1 is included in the set. Subtract one from all numbers.
Here $$$g(i-j , j-1)$$$ corresponds to $$$g(17 , 2)$$$
$$$g( i - (N+1) , j-1) = g(10,2) = 4$$$
So we have safely subtracted all the unnecessary cases where $$$N+1$$$ is a part of the partition. I hope this clears up confusion on this topic.
Thank you, Roundgod, for such a wonderful editorial.
Each and every line of this blog is very informative. Thank you so much.