1107A - Разбиение последовательности цифр
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int q;
cin >> q;
for (int i = 0; i < q; ++i) {
int n;
string s;
cin >> n >> s;
if (n == 2 && s[0] >= s[1]) {
cout << "NO" << endl;
} else {
cout << "YES" << endl << 2 << endl << s[0] << " " << s.substr(1) << endl;
}
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (Ne0n25)
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
long long k, x;
cin >> k >> x;
cout << (k - 1) * 9 + x << endl;
}
}
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
cin >> n >> k;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
string s;
cin >> s;
long long ans = 0;
for (int i = 0; i < n; ++i) {
int j = i;
vector<int> vals;
while (j < n && s[i] == s[j]) {
vals.push_back(a[j]);
++j;
}
sort(vals.rbegin(), vals.rend());
ans += accumulate(vals.begin(), vals.begin() + min(k, int(vals.size())), 0ll);
i = j - 1;
}
cout << ans << endl;
return 0;
}
Tutorial
Tutorial is loading...
Solution (Vovuh)
#include <bits/stdc++.h>
using namespace std;
const int N = 5200;
int n;
bool a[N][N];
void parse_char(int x, int y, char c) {
int num = -1;
if (isdigit(c)) {
num = c - '0';
} else {
num = c - 'A' + 10;
}
for (int i = 0; i < 4; ++i) {
a[x][y + 3 - i] = num & 1;
num >>= 1;
}
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
scanf("%d", &n);
char buf[N];
for (int i = 0; i < n; ++i) {
scanf("%s", buf);
for (int j = 0; j < n / 4; ++j) {
parse_char(i, j * 4, buf[j]);
}
}
int g = n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
int k = j;
while (k < n && a[i][k] == a[i][j]) ++k;
g = __gcd(g, k - j);
j = k - 1;
}
}
for (int j = 0; j < n; ++j) {
for (int i = 0; i < n; ++i) {
int k = i;
while (k < n && a[k][j] == a[i][j]) ++k;
g = __gcd(g, k - i);
i = k - 1;
}
}
cout << g << endl;
return 0;
}
1107E - Вася и двоичная строка
Tutorial
Tutorial is loading...
Solution (Roms)
#include <bits/stdc++.h>
using namespace std;
const int N = 102;
const long long INF = 1e12;
int n;
string s;
int a[N];
long long ans[N][N];
long long dp[2][N][N][N];
long long calcDp(int c, int l, int r, int cnt);
long long calcAns(int l, int r){
if(l >= r) return 0;
long long &res = ans[l][r];
if(res != -1) return res;
res = 0;
for(int cnt = 1; cnt <= r - l; ++cnt){
res = max(res, calcDp(0, l, r, cnt) + a[cnt - 1]);
res = max(res, calcDp(1, l, r, cnt) + a[cnt - 1]);
}
return res;
}
long long calcDp(int c, int l, int r, int cnt){
if(cnt == 0) return calcAns(l, r);
long long &res = dp[c][l][r][cnt];
if(res != -1) return res;
res = -INF;
for(int i = l; i < r; ++i){
if(c == s[i] - '0')
res = max(res, calcAns(l, i) + calcDp(c, i + 1, r, cnt - 1));
}
return res;
}
int main(){
cin >> n >> s;
for(int i = 0; i < n; ++i)
cin >> a[i];
memset(dp, -1, sizeof dp);
memset(ans, -1, sizeof ans);
cout << calcAns(0, n) << endl;
return 0;
}
1107F - Вася и бесконечные кредиты
Tutorial
Tutorial is loading...
Solution (Roms)
#include <bits/stdc++.h>
using namespace std;
const int N = 505;
const long long INF = 1e18;
int n;
long long a[N][N];
int up[N], down[N], k[N];
long long u[N], v[N];
int p[N], way[N];
int main(){
cin >> n;
for(int i = 0; i < n; ++i)
cin >> up[i] >> down[i] >> k[i];
for(int i = 0; i < n; ++i)
for(int j = 0; j < n; ++j)
a[i + 1][j + 1] = -(up[j] - min(i, k[j]) * 1LL * down[j]);
long long res = 0;
for(int i = 1; i <= n; ++i){
p[0] = i;
int j0 = 0;
vector<long long> minv (n + 1, INF);
vector<char> used (n + 1, false);
do{
used[j0] = true;
int i0 = p[j0], j1;
long long delta = INF;
for (int j = 1; j <= n; ++j)
if (!used[j]){
long long cur = a[i0][j] - u[i0] - v[j];
if (cur < minv[j])
minv[j] = cur, way[j] = j0;
if (minv[j] < delta)
delta = minv[j], j1 = j;
}
for (int j = 0; j <= n; ++j)
if (used[j])
u[p[j]] += delta, v[j] -= delta;
else
minv[j] -= delta;
j0 = j1;
}while (p[j0] != 0);
do {
int j1 = way[j0];
p[j0] = p[j1];
j0 = j1;
} while (j0);
res = max(res, v[0]);
}
cout << res << endl;
return 0;
}
1107G - Вася и максимальный заработок
Tutorial
Tutorial is loading...
Solution (Roms)
#include<bits/stdc++.h>
using namespace std;
const int N = int(3e5) + 99;
struct node{
long long sum, ans, pref, suf;
node () {}
node(int x){
sum = x;
x = max(x, 0);
pref = suf = ans = x;
}
};
node merge(const node &a, const node &b){
node res;
res.sum = a.sum + b.sum;
res.pref = max(a.pref, a.sum + b.pref);
res.suf = max(b.suf, b.sum + a.suf);
res.ans = max(max(a.ans, b.ans), a.suf + b.pref);
return res;
}
int n, x;
pair<int, int> p[N];
node t[N * 4];
void upd(int v, int l, int r, int pos, int x){
if(r - l == 1){
assert(pos == l);
t[v] = node(x);
return;
}
int mid = (l + r) / 2;
if(pos < mid) upd(v * 2 + 1, l, mid, pos, x);
else upd(v * 2 + 2, mid, r, pos, x);
t[v] = merge(t[v * 2 + 1], t[v * 2 + 2]);
}
node get(int v, int l, int r, int L, int R){
if(L >= R) return node(0);
if(l == L && r == R)
return t[v];
int mid = (l + r)/ 2;
return merge(get(v * 2 + 1, l, mid, L, min(mid, R)),
get(v * 2 + 2, mid, r, max(L, mid), R));
}
int main() {
scanf("%d %d", &n, &x);
for(int i = 0; i < n; ++i){
scanf("%d %d", &p[i].first, &p[i].second);
p[i].second = x - p[i].second;
}
sort(p, p + n);
for(int i = 0; i < n; ++i) upd(0, 0, n, i, p[i].second);
vector <pair<int, int> > v;
for(int i = 1; i < n; ++i)
v.emplace_back(p[i].first - p[i - 1].first, i);
sort(v.begin(), v.end());
long long res = 0;
set <pair<int, int> > s;
for(int i = 0; i < n; ++i){
s.insert(make_pair(i, i + 1));
res = max(res, 1LL * p[i].second);
}
int l = 0;
while(l < v.size()){
int r = l + 1;
while(r < v.size() && v[l].first == v[r].first) ++r;
long long d = v[l].first * 1LL * v[l].first;
for(int i = l; i < r; ++i){
int id = v[i].second;
auto it = s.upper_bound(make_pair(id, -1));
assert(it->first == id);
assert(it != s.begin());
auto R = *it;
--it;
auto L = *it;
s.erase(L), s.erase(R);
L.second = R.second;
auto nd = get(0, 0, n, L.first, L.second);
res = max(res, nd.ans - d);
s.insert(L);
}
l = r;
}
cout << res << endl;
return 0;
}










Someone help with the solution for problem-B. I can't "easily" get it :( How did it go from the formula to (k−1)⋅9+x
Any number's one digit sum equivalence is equal to number modulo 9
Helpful Link:- https://math.stackexchange.com/questions/1789533/why-is-n-1-mod-91-equal-to-summing-all-digits-till-one-digit-is-left
Assume you understand the given formula.
Then, you will easily find that S(x) repeats every 9 integers.
So, you can write it as my + n, y should be related to k, n should be related to x, m should be a constant.
The numbers 1 to 9 are the first cycle. Its digital roots are itself.
The numbers 10 to 18 are the second cycle.
Randomly pick two integers from the first and the second cycle, throw it into the my + n, you should then get the formula.
Just write a small function to print all results from 1 to 100, you can easily see the cycle pattern exist there. hope this can help.
Problem G:
For every diff[i], I calculated the range in which it is maximum and took maximum suffix from left side and maximum prefix from the right side to calculate the answer.
Before constructing the segment tree,just to verify the logic I submitted the code with O(n) function to calculate max prefix and suffix expecting a TLE, but surprisingly it got ACed. Submission: 49068594
Are the test cases weak or is the time complexity of this solution lesser than O(n^2)
EDIT: neal answered it here
For problem D, the brute force solution apparently runs fast enough.
Yes,my brute force solution runs for 800+ ms.So I don't think this problem is very good and I don't know why this problem's difficulty is 1800. The time complexity just O(n²*c) ,c is the number of divisors of n
c can be treated as a constant.
I think c can't be treated as a constant...c changes when n changes...but certainly , c is always less than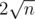 ......
......
On the one hand, if some segment of kind [1+lx , 1 + (l+1)x], where l is the value from the range [0;n/x−1], contains different digits then we cannot compress the given matrix.Can someone explain me this with an example ??
Please.. Someone explain me this with an example too.
for example:- let us assume that the size of given matrix A is 8 and we are using x = 2, then values of Ceil(8/2) = 4,Ceil(7/2) = 4 which means B[4][4] is equal to A[8][8], A[7][8], A[8][7],A[7][7]. which will not be possible if these values are different.
Problem G: Solved it using segment trees(max segment tree) and lazy updates. Start iterating i from 1 to n. For a fixed i, a node j(<=i) will contain the answer for the segment j to i. So at each iteration, make a query from 1 to i. For the update part, when going from i to i+1, add (a — c[i+1]) to the range (1 to i) and maintain a stack to store the gap values for the range. For the stack update, if the new value i.e. (d[i+1] — d[i])^2 is smaller than the top value of stack, just add the negative value of it to the stack with it's range and also update it's value in the segment tree. If the new value if larger than the top value of stack, keep popping the top value(these values also need to be updated in the segment tree) until the new value is smaller than the stack's top value. Submission: 49103066
Why additional time is not given for Java programmers? Even the solution given in editorial for problem D is giving TLE in Java.
In task F we don't have to pick every credit, so shouldn't the formula be min(0, rest of formula)? Every Hungarian algorithm (that I found) assign all of n elements. Or just b[i]*k[i]<=a[i], but the statement doesn't include it?
Regarding the tutorial for problem E.
I think it should be l ≤ mid ≤ r instead of 1 ≤ mid ≤ r here.
also mid<=r only if cnt=1
what is the difference between these two?
i mean is there something wrong with the second one?
Someone please explain the solution for problem-E, I didn't understand it from the tutorial.
Made a solution just doing recursion on strings to show the idea (solution). I think this is a bit easier to follow.
Nice Approach, I tried this and got AC, but before that I had tried to recursively remove each block of consecutive digits(same 1s or Os). Algorithm is right but I got TLE, I don't understand why it is. Can you explain what happen? HERE IS MY CODE: https://codeforces.com/contest/1107/submission/49218582
The difficult part of this problem is not really to calculate the answer but to do it quickly. The reason why my code doesn't get TLE is that I practically only modify the beginning of the string, and if you think about it all the strings that is created will basically be a substring of the original string (except for the beginning part). So the number of strings I create are very limited.
In your code you are not doing it nearly as neatly because you are deleting parts of the string everywhere (not just in the beginning). So you will create a ton of different strings, probably exponentially many, and because of that get TLE.
Yeah I understand your code, that is your state either is substring of original string or combination of two substrings of original string. The number of different substring is nC2 ~ N^2 and the number of combination of 2 substrings is (N^2)C2 ~ N^4, so your complexity is O(N^4).
And my code may be up to N! So it gets TLE.
Thanks for your help!
To be technical, its not either a substring of the original or a combination of two substrings. It is always a string on the form '0...0' + S[a:b] or '1...1' + S[a:b] so there are n3 possible different strings.
Yep, sorry. So it runs in N^3 right?
The algorithm will ever only visit n3 strings but for each string it will do at most n2 work. This is because for each string it might need to lookup n strings in a hashtable. So it runs in n5 with a very good constant, this could be lowered to n4 by playing around with indices instead of strings.
I will give a proof in this comment on why the formula for 1107B - Цифровой корень works.
To see that the formula is true you can prove that and
and 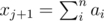 gives the same value or it is invariant under the formula. In the case of xj substracting 1 means that the trailing 0s become 9s so the disappear modulo 9 and if k is the first non-zero digit of xj then its value will decrease by 1. Then we can do something like this:
gives the same value or it is invariant under the formula. In the case of xj substracting 1 means that the trailing 0s become 9s so the disappear modulo 9 and if k is the first non-zero digit of xj then its value will decrease by 1. Then we can do something like this:
It's not hard to see that given a b-ary number system where b is a positive integer if we define a similar process then the number x will end up in Sb(x) which can be characterized like:
The proof is the same as the above just replace 10 with b and 9 with b - 1.
good
Can someone please explain the editorial of E in more detailed way ?
Can someone explain why DP calculation in E is correct i.e. why there exist 'mid', why optimal solution for DP doesn't contain more than one segment which will lead to 'cnt' number of 'dig' instead of just a segment [mid, r]?
Upd: Got it.
vovuh In D why can't we use binary search across the divisors of n to find x?
Because the function isn't monotonic. For $$$n=12$$$ if the answer for $$$2$$$ and $$$4$$$ is true then it is not necessary that for $$$3$$$ the answer also will be true.
Example (uncompressed):
Thanks
A different approach for problem D here
Using gcd
interesting approach.
Whosoever solves problem E.
Please let me know how the complexity of the solution is O(n^4).
For Problem G: I used Kadane's algorithm but it gives wrong answer on test 7 and test 36 only. Could anyone point out the issue with this approach. Code with some comments.
Simple bruteforce is enough for 1107D — Compression. https://codeforces.com/contest/1107/submission/160440328