Hi!
XIX Open Cup Grand Prix of Belarus takes place on Sunday, February 17, 2019 at 11:00 MSK.
The contest writers are Mediocrity, gepardo, greencis, kimden, and kefaa.
Links to the contest: division 1, division 2. Please do not solve the contest if you solved it in Petrozavodsk.
Let's discuss problems after the contest. Good luck!
UPD. Editorial











On the contest page it says: "The virtual contest is in progress. You are not allowed to participate".
Is the contest not loading for anyone else as well?
1) Was the intended solution for J just to precalculate somehow count of all primes and primes of form 4k + 3 up to 1011? If yes, how to do it fast enough?
2) How to solve B? Is there any way to do it without calculation of polynom (x - c1)... (x - cn), where ci = di - dmin?
B: the cumulative distribution function of the answer is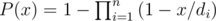 when
when 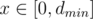 , you need to calculate it multiplying polynomials with divide&conquer. Then you find
, you need to calculate it multiplying polynomials with divide&conquer. Then you find 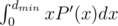 in linear time.
in linear time.
Whoops, yeah, I'm definitely lacking calculus skills. Don't look into the first revision, please)
There were two intended approaches for problem J. One of them is to precalculate count of jimp numbers on blocks of length ≈ 107 and count the rest using the segmented sieve of Eratosthenes. The second approach is quite complicated. It involves dynamic programming which does sort of "sieve of Eratosthenes" to calculate how many numbers are either prime or not multiple of any of the first k primes. More details may appear later; we would also appreciate if the teams shared ideas of their accepted solutions without precalc.
Basically, you just need to run the segmented (or block) sieve of Eratosthenes. You can read more about it, for example, here. It works about 20 minutes for the authors to do all precalculations. Note that it's not necessary to calculate primes of form 4k + 1 and 4k + 3 separately, but just all jimp numbers together.
What's the expected complexity of C? My O(NlogNlogMAXVAL) gets TLE at test 55. Is there an O(NlogN) solution?
Did you write binary search + segment tree with arithmetic progression update for TLE solution?
No.I used static convex hull and binary search.
what is static convex hull , from where u study these things . i have never heard of it
You are too noob to know this. Play more MOBA or BR, then you will eventually know.
Well, is it possible to write a segment tree that supports:
Initializing values (i.e. build function)
Range update with arithmetic progression (a[l] += d, a[l+1] += 2d, ...)
Range min/max query
My code could do the second and third type of queries but I don't know why my code didn't work. The idea was keeping the first element of AP, the difference of AP, and min/max of range.
Can you please explain (or provide some links) how to do both 2nd and 3rd type of queries? I tried to find anything about that but failed. The main question is how to recalculate min/max of range after adding new progression?
After updating with AP, I updated the min/max element with the first and last element of range but that is totally wrong. However, in the task, I only needed to update range [1, n] in which the aforementioned method works because adding new AP to some AP derives new AP. Though initializing elements ruined everything since they are not AP every time.
So, the question remains open, I also couldn't find any information from the internet.
lazy Propagation. I couldn't find it on internet, but it works.
Can you explain how?
Sorry, I didn't notice the arithmetic part. However, I'll keep thinking about it.
Some implementation issues, I presume? The authors' solutions have complexity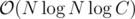 , too, and we do not know faster solutions. If someone does, please tell us here.
, too, and we do not know faster solutions. If someone does, please tell us here.
Can you please tell the author's approach?
Our solution with dynamic CHT + parallel binary search also failed the time limit. After about 6 unsuccessful attempts of changing the number of iterations on the binary search, we decided to implement stack-like CHT + parallel binary search, which fit into time limit (even though it's the same complexity, binary searching on array vs set is faster).
Is it really necessary to put such tight TL constraints, so that one O(Nlog(N)log(1 / eps)) solution fails and another O(Nlog(N)log(1 / eps)) solution passes? (especially as the intended complexity of the solution was this)
My solution with 60 iteration runs in 2.4s, so TL is not very lenient. But I don't see any reason for setter to test and pass a solution which is much more slower (and harder) than reasonable implementation? I believe Dynamic CHT would fail even if TL = 10s.
Btw, what I actually didn't liked was the ai ≤ 109, which makes n × n × ai to overflow int64. I was forced to use doubles because of it.
I didn't use dynamic CHT, rather building my convex hull was done in O(n). My complexity came to be O(NlogNlogC) due to a binary search and a seperate ternary search in CHT for the query.
How to solve E?
E: The sum of distances is minimized on the centroid of the tree. So if an edge splits the tree into components of size k and n - k it adds min(k, n - k) to the cost. There are ways to split the vertices in 2 sets of size k and n - k, and kk - 2(n - k)n - k - 2k(n - k) trees with an edge connecting those 2 sets. For each such tree we add min(k, n - k) to the answer. The solution works in
ways to split the vertices in 2 sets of size k and n - k, and kk - 2(n - k)n - k - 2k(n - k) trees with an edge connecting those 2 sets. For each such tree we add min(k, n - k) to the answer. The solution works in 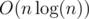 . It seems that the only reason for n ≤ 5000 is so I spend half the contest optimizing
. It seems that the only reason for n ≤ 5000 is so I spend half the contest optimizing 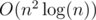 solution.
solution.
too many errors in samples :(
Could you please tell which particular problems had errors in their samples? We are only aware of typos in Notes section in problem C, where 3 values in sample explanation are wrong. But it seems that it didn't cause any troubles for many teams in passing problem C. (UPD: Div2 problems had some typos, too.)
Anyway, sorry for the inconvenience, we'll be more careful next time.
(Div2) For example O, P, i catch strange "Check failed" in G. It's not problem a big problem for a lot of people, that's just affected me enough, bcs my incorrect program gave the same result for incorrect sample :)
How to solve A?
First, ask about all the vertices. Then for each i ask about all the vertices except the i-th one. If the area decreases, then i-th vertex is the vertex of convex hull. Notice that vertices of convex hull are in the same order as the vertices of the polygon. Now we know that convex hull is p1, p2, ..., pk. To find the area of the polygon we need to subtract from area of convex hull areas of polygons of the form pi, pi + 1, ..., pi + 1 - 1, pi + 1. We can find those areas recursively with the same idea.
Also, if the area of convex hull is 0, we should set the area of polygon to 0 and stop, otherwise we can ask about this polygon infinitely.
How do you show that this asks no more than (n(n - 1)) / 2 queries? We could show O(n2) by arguing about how many times a vertex can be a "hole" (ie. the vertex in the except clause) -- but couldn't get the constant.
Also, did anyone else get Presentation Error? We checked number / validity of queries with asserts, and can't figure out why it's happening.
In each recursion call we ask one question about all vertices and one question about each vertex which is not on convex hull. So, for each vertex the number of questions about it is the depth of recursion when it becomes on convex hull. On the first recursion call we find at least 3 vertices on convex hull. Then on each depth of the recursion we find at least 1 vertex on convex hull. Also there are no more than n - 2 recursion calls, because on each recursion call we find at least one vertex on convex hull, but on the first one we find 3. So overall the number of questions is no more than 3 + 2 + 3 + 4 + ... + (n - 2) + (n - 2) = n(n - 1) / 2 + 1. Actually the number of queries is a bit less because when there are only 3 remaining vertices, we know that all of them are the convex hull.
What is the solution to D?
Auto comment: topic has been updated by kimden (previous revision, new revision, compare).
Will the problems be added to GYM?