Let’s look at all restraunts, where Rabbits can have their lunch. Let’s calculate the answer for all restraunts and choose the maximulm value among of them. We need to use formula descrbed in problem statement to calculate the answer for some particular restraunt. Time complexity of this solution is O(N).
Let’s calculate the number of letters with odd number of occurrences in s. Let this value be equal to k.
If k = 0, then first player can win immediately: he can easily build palindrome, placing equal letters in different sides of resulting string (he always can do it, because total number of all letters is even).
If k = 1 then first player can win immediately again; at first he builds palindrome from letters with even number of occurrences in s; after that he inserts the rest of the letters in the middle of built in previous step string.
Let’s proof very useful statement. If k > 1 our problem has the following solution: if k is even, than second player is winner; otherwise, first player is winner.
Let k = 2. At the beginning of the game first player can make move of two types.
Using move of first type first player can decrease k to 1 by erasing one appearance of letter with odd number of occurrences. But this move leads him to defeat, because after this move second player can build palindrome.
Using move of second type first player can increase k to 3 by erasing one appearance of letter with even number of occurrences. In this case second player can make similar move — he will erase the same letter. Since the number of moves of this type is finite, sooner or later first player will have to make a move of first type. After this move he loses immediately.
So, if k = 2, than second player is a winner.
Let k = 3. First player can decrease k to 2 by erasing the letter with odd number of occurrences. If second player will try to increase k to 3 again by erasing the similar letter, first player can decrease k to 2 again (he erases the same letter again). It’s easy to see that the last move in this sequence of moves will be the move of first player. So, first player always can change the game in such a way that k = 2. This position is losing position for second player and winning position for first player.
Now we can easily proof our statement for any k using mathematical induction.
So, we have quite easy solution with time complexity О(|S|).
C. Little Girl and Maximum Sum
Lets calculate for each cell of the initial array the number of queries that cover this cell. It’s claimed, that we should associate the cell with bigger value to the cell with bigger value in initial array. More formally: suppose b is an array, in i - th cell of which is written the number of queries that cover i - th cell. Suppose а is an initial array. Let’s sort those arrays. It’s claimed, that the answer in this case can be calculated with following formula: 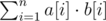
Let’s proof this statements. We will take a look at some indexes i < j, and at elements, corresponding to shis indexes a[i], a[j] , b[i], b[j] (a[i] ≤ a[j], b[i] ≤ b[j]). Those elements add to the answer the following value: a[i]·b[i] + a[j]·b[j]. Let’s swap a[i] and a[j]. Now those elements elements add to the answer the following value a[i]·b[j] + a[j]·b[i]. Let’s take a look at the following difference:
a[i]·b[j] + a[j]·b[i] - a[i]·b[i] - a[j]·b[j] = b[j]·(a[i] - a[j]) + b[i]·(a[j] - a[i]) = (b[j] - b[i])·(a[i] - a[j]) ≤ 0.
So, swapping of two elements leads us to nonincreasing of the total result. This means, that our arrangement is optimal.
Now we need to calculate array b fast enough.
For this purpose one can use different data structures, which support segment modifications (segment tree, Cartesian tree and so on). But there exists much easier method.
Let’s create some array d. When we have query li, ri, we should increase value d[li] by 1 and decrease value d[ri + 1] by 1. In such a tricky way we increase all elements in segment [li;ri] by 1 After processing all of the queries we need to make a loop, which visit every element of array d. In this loop we can easily calculate all elements of array b.
Now we are ready to get the final answer. The complexity of author’s solution is O(NlogN + Q)
D. Little Girl and Maximum XOR
To be honest, I am surprised that problem D had so many accepted solution during the contest. The author’s solution uses dynamic programming. In this editorial I’ll explain this solution.
First of all we should convert L and R to the binary numeral system. Now we can solve our problem with dynamic programming, using the following state d[p][fl1][fr1][fl2][fr2], where p is current position in binary representation of our numbers a and b (this parameter is in range from 0 to number of bits in R), fl (0 or 1) is a variable, which shows if current value of а is strictly greater than L, fr1 (от 0 до 1) is a variable, which shows if current value of а is strictly less then R, fl2, fr2 are variables, which show the similar things for b.
Let’s use recursion with memorization for our solution.
Let’s define the base of recursion. If we have looked through all the bits, we should return 0.
Let’s define a recursive transition. We need to know, which bits we can place into binary representation of number а in p-th position. We can place 0 if the following condition is true: p-th bit of L is equal to 0, or p-th bit of L is equal to 1 and variable fl1 shows that current value of a is strictly greater then L. Similarly, we can place 1 if the following condition is true: p-th bit of R is equal to 1, or p-th bit of R is equal to 0 and variable fr1 shows that current value of a is strictly less then R. Similarly, we can obtain, which bits we can place into binary representation of number b in p-th position.
Let’s iterate through all possible bits’ values and check the result of xor operation. If it is equal to 1, we should add to the answer corresponding power of 2. We also need carefully recalculate values of variables fl1, fr1, fl2, fr2. We should choose maximum answer from all valid options.
Initial state for our recursion is (P,0,0,0,0), where P is number of bits in R.
I hope, my code will clarify all the obscure points.
I also want to say, that this approach is in some sense universal and can be applied to many similar problems, like this one
The complexity of algorithm is O(logR)
In Russian thread I saw another really nice solution, so I decided to include this solution to the editorial.
First of all, if L = R, than the answer is 0.
Now let’s consider case with L ≠ R. Let Ri be the i-th bit of R, Li be the i-th bit of L. Let’s define p as largest number such as Rp ≠ Lp (we use 0-based indexation). Let’s take a look at all numbers in range [L;R]. It’s easy to see, that bits, that are higher than bit with index p are equal for all this numbers. Thus, those bits can not affect our answer, because their xor will always equal to 0.
Let’s build numbers a and b in the following way:
1) a: bits which are higher than bit with index p are equal to the corresponding bits of L, p-th bit is equal to 0, the rest of bits are equal to 1.
1) b: bits which are higher than bit with index p are equal to the corresponding bits of L, p-th bit is equal to 1, the rest of bits are equal to 0.
It’s easy to see, that a and b both lie in range [L;R]. It’s also easy to see, that xor of this numbers sets all bits, that are not higher than bit with index p to 1. So, our answer is maximum possible and is equal to 2p + 1 - 1
The complexity of algorithm is O(logR)
Java solution from AlexanderBolshakov
We can iterate through value of p using binary search. We can achieve time complexity O(log(logR)) in this way, but it wasn’t required during the contest.
E. Little Girl and Problem on Trees
One can see, that our tree is a set of chains, each of which starts in the root.
First of all we need to decompose our tree in chains using, for example, depth first search. For each vertex we should find out it’s depth and number of chain, which contain this vertex. For each chain we’ll use some data structure, which can fast enough change it’s elements and fast enough answer to the range sum query. For example, we canuse Binary Indexed Tree (BIT). We also need to create one BIT for root. This BIT is global: it’s information is actual for all the chains
Let’s remember problem С. In that problem we used array d for processing all the queries. We need to know values of elements of array b in that problem after processing all the queries. In this problem queries are online. That’s why we need to use BIT; it allows to change element and answer range sum query in O(logN) time.
Let’s learn, how to process queries, which require modification and queries, which require finding the element, using BIT.
BIT can make two types of operations:
add(x, y) — add value y to element with index x
find(x) – finds sum in range from 1 to x
Let’s consider, that we need to add value val to all elements in range from l to r . Than we should just make operations add(l, val) and add(r + 1, - val).
Let’s consider, that we have query which require printing the value of element with index v. Then we should just make operation find(v).
Now let’s go back to the initial problem.
During the processing query of type 0 we should check, if it affects the root. If query affects the root, we should carefully process this query in our chain and make necessary changes in root’s BIT. Otherwise we just process query in our chain.
During the processing query of type 1 we should just find corresponding sums in root’s BIT and in BIT for our chain. We should print the sum of this values.
Time complexity of this solution is O(N + QlogN)
That’s all. I’ll be very glad to answer to your question in comments.











can somebody post the tutorial in English !! thanks much appreciated :)
I'll translate the editorial as soon as possible. I'll try to do it today.
In maximum XOR question: In the bit representation of l and r if the leftmost difference in their bit patterns occurs at the nth position isn't the answer simply 2^n-1?
It's true (if n is 1-indexed, of course). I described this solution in editorial.
Nice editorial and clear explanation!! One thing that I want to know that what the following code segment do? And how can I have my own "whatever it is called :p"? Thanks :)
It's a preprocessor definition. You can read about it here: http://msdn.microsoft.com/en-us/library/hhzbb5c8(v=vs.80).aspx or google it elsewhere.
This block redirects stdin to file and starts measuring execution time of my program. Because of preprocessor definitions, this code does not execute on a judging system, but I can use it locally.
wah, thanks for this editorial, the explanation is very clear :)
Love the alternate solution to D !
Guess it could be applied to a harder question where L and R were represented in binary form with a string of length <= 10^6.
I wrote a detailed post about Problem D here. Let me know if you have any doubts or want to discuss further :)
nice explanation bro thanks
In the code for E, can you please explain what the variable t is doing ? Not able to understand.
The variable t holds all of the binary index trees (one for each chain and one for the root)
Wow, it's nice to see that someone is actually working on the problems from that contest even after all these years :)
Thank you for your reply. I even wrote a blog post about your D :)
I'm trying to do it with segment trees as I'm not that comfortable with BITs. I'm struggling with dynamically allocating memory to each tree :\
Segment trees are also perfectly suitable for this task. You can easily allocate memory in a very similar manner — just store segment trees in vectors and resize them appropriately (usual stuff — suppose you have n elements in your tree, then find the smallest k such as 2k ≥ n and allocate memory for 2k + 1 elements)
Thank you for your assistance.
Please check my blog about your problem :)
Use some mathematics for Div2 D and you will be able to find the solution in just few lines of code. My Solution:- 72932119 For a detail explanation reply to this comment.
why is my code getting wrong answer for c question test 7 .. i have done similar to what is mentioned in editorial https://codeforces.com/contest/276/submission/94873267
Can Div2 C be solved using segment tree ? I tried but getting TLE on testcase 7
Yes, I solved it based on segment tree. At first, we use segment tree to find out the number of queries for each element. Then, we could adopt a greedy algorithm to compute the final answer.
same problem i m facing
Nice explanation for problem E.
hello i'd like to share my solution for problem C