Hello, Codeforces!
Recently I was solving max-flow problems, here is one of the problems I can't solve.
You're given a network with min and max constraints on the edges. For simplicity suppose all the edges have capacity=1. For example, you have the following network:
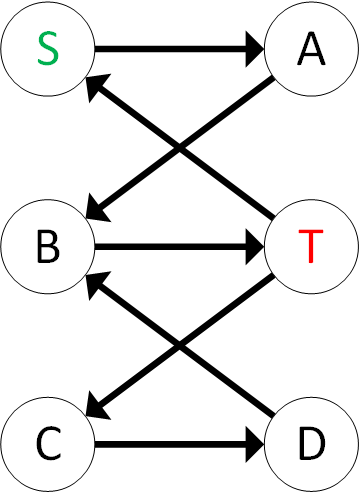
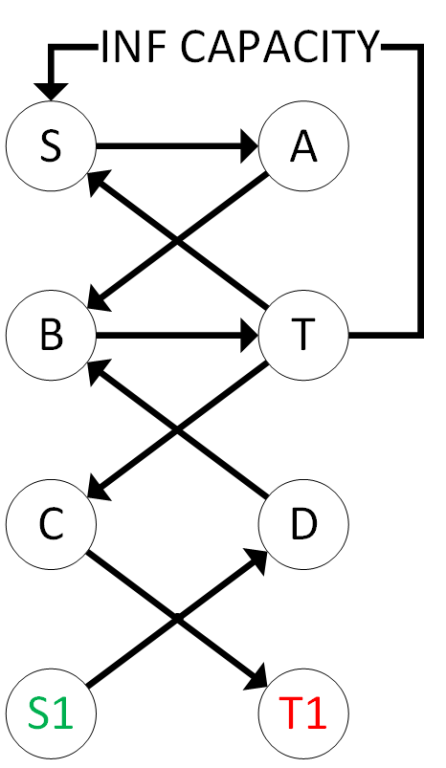
We want to put a lower constraint on the edge C->D so that it's min=1 and check whether there exists a flow from S to T which uses the edge C->D. Note that it's unable in the given example. To find max flow on this network, we should change it slightly to remove lower constraints from the edges (algorithm is here (on russian): https://e-maxx.ru/algo/flow_with_limits). After these changes we will get the following network (I removed edge C->D with capacity 0 from the image):
Now run any max-flow algorithm and it will find the next flow (yellow edges are used edges):
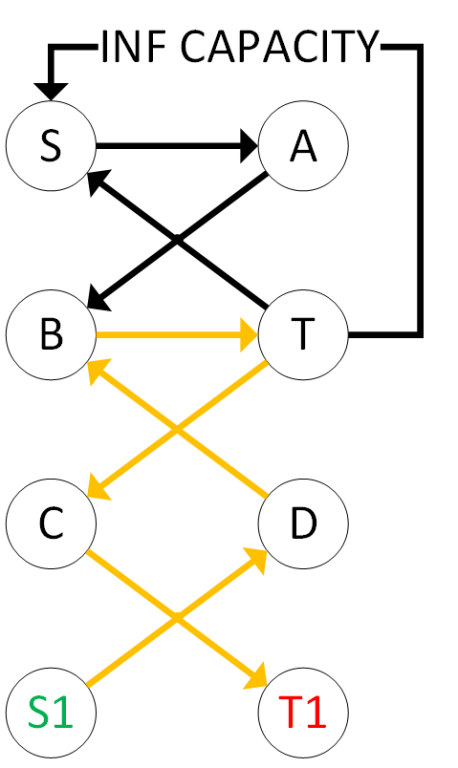
As you can see, the flow is found and it means that we can use these edges in the original network and we will get the flow from S to T with edge C->D. Restore the original network now:
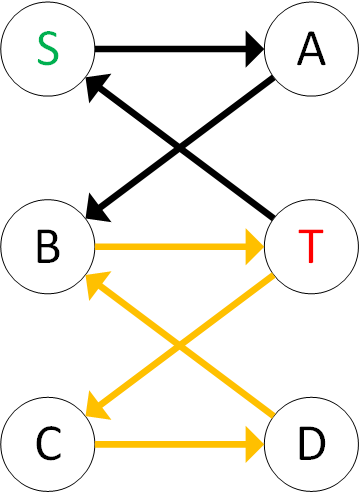
But, as you can see, this is not the flow from S to T.
So, my question is: How to check lower contraints in networks with cycles?











This is a valid flow from $$$S$$$ to $$$T$$$ of size 0. It satisfies the capacity constraint and the conservation of flows.
In general, any flow can be decomposed into paths and cycles. This flow contains a single cycle.
Ok, now I see that the found flow is valid. Anyway, is there a method to check if we can satisfy the lower constraints with the flow which starts in
S, ends inTand uses at leastmin capacityof every edge?I mean, the value of outcoming flow fromSis equal to sum of min capacities, and same for incoming flow inT.EDIT: Of course, not the sum of min capacities. I meant that what if we don't want to include any cycles (circulations) which are independent of flow from
S.This one looks NP-hard. There's a reduction from Hamiltonian Path problem:
Take any undirected graph $$$G$$$ with $$$n$$$ vertices. Create a directed graph $$$H$$$ in the following way: for each $$$i$$$ from $$$1$$$ to $$$n$$$, create two vertices $$$a_i$$$, $$$b_i$$$ and create a directed edge $$$a_i \to b_i$$$ with mincap=maxcap=1. For each edge $$$uv$$$ in the original graph $$$G$$$, add two directed edges to $$$H$$$: $$$b_v \to a_u$$$ and $$$b_u \to a_v$$$. Finally, set $$$S=a_1$$$ and $$$T=b_n$$$.
Now, we can see that there exists a flow with your property if and only if there is a Hamiltonian Path between $$$1$$$ and $$$n$$$ in $$$G$$$.
(I hope this is correct. XD)
I created this graph in almost the same way you explained) The only difference is that not all the edges $$$a_{i} \to b_{i}$$$ have mincap=1.
And yes, surely now it looks like NP-hard.
Thanks for your reply.