Here is the editorial for Round #174. Thanks for participating. We hope you enjoyed the problems! :)
Div2 A
We didn’t expect this problem to be so hard :(. This problem can be solved by brute forcing. For any x, you can compute 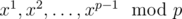 in O(p) time (iteratively multiply cur = (cur * i) % p, not use pow in math library!), so overall brute force will be O(p2) time.
in O(p) time (iteratively multiply cur = (cur * i) % p, not use pow in math library!), so overall brute force will be O(p2) time.
Note: there is actually 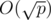 algorithm.
algorithm.
The problem was written by abacadaea.
Div2 B
We first note that players who have folded do not affect our desired answer. Then, we can do casework on the number of players who are currently “IN”. If no cows are “IN”, then all the players who are “ALLIN” can show their hands. If exactly one cow is “IN”, she is the only one who can show, so the answer is 1. If two or more cows are “IN”, no one can show their hands. Then we simply count the number of cows of each type and check for each case. The total runtime is O(n).
The problem was written by scott_wu.
Div1 A / Div2 C Consider the problem with only queries 1 and 2. Then the problem is easy in O(n): keep track of the number of terms and the sum, and you can handle each query in O(1). But with query 3 we need to also be able to find the last term of the sequence at any given time. To do this, we keep track of the sequence di = ai + 1 - ai for i = 1, 2, ..., s - 1, and as, where s is the length of the sequence. Notice that query 2 only modifies one value of di, and queries 1 and 3 are easily processed and able to update this information. This gives us an O(n) algorithm.
One can also use a fenwick or segment tree to compute the last element, but it’s not nearly as nice :).
The problem was written by abacadaea.
Div1 B / Div2 D
First, suppose we only have the sequence a2, a3, …an. We note that the current state is only determined by the location and the direction we are facing, so there are only 2·(n - 1) states total. Then, we can use DFS with memorization to find the distance traveled from each state, or - 1 if a cycle is formed, in O(n) time. Now, when we add a1 into the sequence, we essentially only need to give the distance traveled starting from each state facing left. The only difference is that if we ever land on a1 again, there must be a cycle, as we started on a1. Using this, we can solve the problem in O(n) time total.
The problem was written by scott_wu.
Div1 C / Div2 E
Imagine the problem as a graph where coins are the nodes and Bessie’s statements are directed edges between coins. Because of the problem conditions, the graph must be a set of cycles and directed paths. If there are any cycles in the graph, the answer is clearly 0.
Then, suppose we have a path p1, p2, …pk in the graph, where it is known that we have more coins of type p1 than of type p2, more of type p2 than of type p3, and so on. The key observation in this problem is that this is equivalent to having k independent coins of value {a(p1), a(p1) + a(p2), a(p1) + a(p2) + a(p3), …}. The first coin in our new list represents how many more coins of type p1 than of type p2 we have, the second coin in our new list represents how many more coins of type p2 than of type p3 we have, and so on. However, we must be careful to note that we need at least one of each of the new coins except for the last one, so we can subtract their values from T before doing the DP.
After creating our new set of values, we can run the DP the same way we would run a standard knapsack. This algorithm takes O(nt) time total.
The problem was written by scott_wu.
Div1 D
Let ν2(n) denote the exponent of the largest power of 2 that divides n. For example ν2(5) = 0, ν2(96) = 5. Let f(n) denote the largest odd factor of n.
We can show that for fixed ai, aj(i < j), we can construct a cool sequence ai = bi, bi + 1, ... bj - 1, bj = aj if and only if 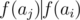 and either ν2(ai) + j - i = ν2(aj) or ν2(aj) ≤ j - i - 1. Proof here
and either ν2(ai) + j - i = ν2(aj) or ν2(aj) ≤ j - i - 1. Proof here
With this observation, we can use dynamic programming where the kth state is the maximum number of ai (i ≤ k) we can keep so that it is possible to make a1, ... ak cool. The transition for this is O(n), and the answer is just n - max (dp[1], dp[2], ..., dp[n]). This algorithm is O(n2).
The problem was written by scott_wu.
Div1 E
This will go over the basic outline for solution.
We can show that the answer is 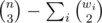 where wi is the number of wins cow i appears to have. Proof here
where wi is the number of wins cow i appears to have. Proof here
Now sort the skill levels of the cows (the order of the si doesn’t actually matter). s1 is lowest skill. Now consider an n × n grid where the ith row and jth column of the grid is a 1 if the match between cow i and cow j is flipped. The grid is initially all zeros and Farmer John’s query simply flips a rectangle of the form [a, b] × [a, b].
We can process these queries and compute the number of wins for each cow using a vertical sweep line on the grid and updating with a seg tree on the interval [1,n]. The seg tree needs to handle queries of the form \begin{enumerate} \item Flip all numbers (0->1, 1->0) in a range [a, b]. \item Query number of 1’s in a range [a, b]. \end{enumerate} Note that given this seg tree we can compute the number of wins for each cow at every point in the sweep line as (Number of 1’s in range [1,i — 1]) + (Number of 0’s in range [i + 1, n]). There are O(m) queries so this solution takes 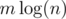 time.
time.
The problem was written by abacadaea.










Wikipedia says that the number of primitive roots is phi(phi(n)) where phi(n) is Euler function.
Added it in. :) See link in the post.
Super fast editorial, thanks!
We didn’t expect this problem to be so hard :(this is not hard, but many contestants faced problem with understanding it.
The fastest Editorial in codeforces I have ever seen. Thanks problem writers :)
Will SQRT decomposition work out in div2_C?
Can someone please help.I was unable to pass the pretests for div 2 problem C . Here is my code. I tried it with segment tree. I'm not experienced with segment tree. I've only used them once or twice.This code got WA in pretest 9.
Didn't use long long and got WA.... :'(
Please tell me, for the problem A, why 1 is primitive root for 2, as test #9 states.
because set {x^1-1 ... x^(p-2) — 1} is empty, so for every element of it it's true that it doesn't divided by 2.
IMO, this set is {1^(2-2)-1} = {0}, and 0 is divided by any natural number.
In that set only elements with power
xthat 1 ≤ x ≤ p - 2. There's no suchxThe problem statement reads: "a primitive root is an integer x (1 ≤ x < p) ... "
... such that none of integers x - 1, x2 - 1, ..., xp - 2 - 1 are divisible by p, but xp - 1 - 1 is.
OK, I see. Thanks!
you're welcome
Div1,C should work (a more general algorithm) even if Bessie's information creates an arbitrary DAG, right?
No, if there are constraints
coins[a] < coins[c]
coins[b] < coins[c]
the generalized algorithm I think you have in mind would never produce solution where coins[c] = 1 (which is legal and may be optimal).
What about such algotithm: build a DAG where a -> b if coins[a] < coins[b], then do topsort and update minimum needed values in topsort order in a manner
if a -> b, coins[b] = max(coins[b], coins[a]+1)
with all coins initialized to 0 at first. Then replace every coin V value with the sum of values of all coins we can reach from V and fill our knapsack using coins in topsort order.
Should it fail in the case of general DAG? Your case is handled correctly: after updating all minimum values coins[a] = coins[b] = 0 and coins[c] = 1.
This algorithm won't produce soluion 2,2,3.
Each "a" coin would be worth a+c, each "b" b+c and "c" would remain unchanged.
Having coins[a] = coins[b] = 2 would be worth >= 2*(a+c) + 2*(b+c) = 2a+2b+4c, meaning 2a+2b+3c is not possible, while it should.
Thank you, I see a mistake now.
Ah, right. Arbitrary forests, then (where a->b if coins[a] < coins[b]).
Div1 A / Div2 C
My submission passes 9 testcases , and then gives an erroneous answer on 10th testcase , with the following verdict :
That's why I think it's unlikely for my solution to be completely wrong. May someone take a look at that submission (it's an unnecessarily complicated segment tree solution) and tell what's wrong with it?
Did you remember to reset the offset array after each element-delete command?
You can see my two similar submissions:
Wrong Answer submission: 3344719
Accepted submission: 3344780
There is a mainly difference on Case 3:
I forgot this sentence so I had to go back to div2.
Can you please explain your algorithm ie update and query ?
It's a typical segment tree with lazy tag.
Maybe there is a bug in your segment tree code.
Your program can't pass the following data:
The output should be:
Below is my solution for the Div 2 A problem. Can someone let me know what is the bug in the solution, it gives an incorrect answer?
#174-Div 2- A
I am trying to follow a brute force algorithm to solve.... This problem is driving me nuts!!...
You made the mistake most people who failed the problem made. "qu *= x;" will overflow for like p >= 15 or something. You need to do qu = (qu * x) % p; :)
qu = (qu * x) % p; Is incorrect with regard to what is mentioned in the question. Since the problem mentions (x^k — 1)is not divisible by p. So why do we need to calculate (x^k) % p.?
So later we can check whether qu = 1. (If qu = x^k % p = 1, that means (x^k — 1) % p = 0 aka (x^k — 1) is divisible by p.)
I can't understand the solution of Div2 D, who can explain it :)
I write a Chinese editorial for div1 ..anyone if need can visit here http://www.cnblogs.com/lzqxh/archive/2013/03/19/2969723.html
For problem Div1 A / Div2 C , can someone list the segment tree solution ? I've a solution that isn't working for certain cases
http://codepad.org/2MiT91wB
I haven't done it with segment tree. I used simple 2 arrays. 1st for the input of the elements(arr) and another for the segments increase case(arr1) So we know that each deletion query is from last only... we just keep updating both arr[curr_length] = 0, and arr1[curr_length-1] += arr1[curr_length]. In this way, we keep the updated amount for the last element always. Check the C++ code : https://codeforces.com/contest/283/submission/78512329.
Wow, nice solution! Thanks a lot.
who can explain the solution of problem div2 D in more details?
check out this solution. Its easy to understand.
Square Root Decomposition is ideal for Div1 A / Div2 C.
Anytime there are operations which change data from indexes 1 to n, applying Square Root Decomposition is a good option.
Basically what we do here is split the n numbers into blocks of sqrt(n). Maintain another "block array" with size sqrt(n). If there is a query of type 1 to add y to first x numbers, then we dont traverse numbers from 1 to x. Instead we only traverse 1 — sqrt(x) elements of the block array, add y only to these and for all the left over numbers ( x % sqrt(x)) traverse numbers one by one and add y to each. Query 2 is straightforward, simply add the number to your array and increase size by 1. For query 3, you need to make all pending changes to the last block (sqrt(n)) numbers as the last number is part of the last block. So traverse all elements in the last block, add any value that exists in the corresponding index of the block array, make this index of the block array 0 and then remove the last value.
For each type of query at worst we will be doing sqrt(n) operations.
Implementation here : https://codeforces.com/contest/283/submission/48110897
Someone please explain Div1A using difference array.
Div2 D/Div1 B. Heavily commented and explained.
Can someone please explain Div 2 D Cow Program in little detail ? I don't understand the editorial for this problem.
Recently I was trying to solve this problem as well, and I think I have got what the tutorials mean.
For any given a[1] (note that the index starts from 1), we should first always implement an operation of addition, and then we will reach some position with a[1] + 1. The key observation is that no matter what value of a[1] is given, we could compute all the value of y as if we 'start' from any position of 2, 3,..., n in previous (here we consider a[1] + 1 as the beginning position).
Notice that we could reach some position by '+' or '-', and thus we use dp[i][0 or 1] to denote the value of y, when we start from position of i, by '+'(1) or '-'(0). For more details, you could check my submission 91858312 with some comments, and if you still have questions about this problem, you are welcome for discussion :D