Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
t = int(input())
for i in range(t):
x, y = map(int, input().split())
if(x - y > 1):
print('YES')
else:
print('NO')
Idea: Neon
Tutorial
Tutorial is loading...
Solution (Ne0n25)
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < int(n); i++)
const int N = 100 * 1000 + 13;
int n, r;
int a[N];
void solve() {
scanf("%d%d", &n, &r);
forn(i, n) scanf("%d", &a[i]);
sort(a, a + n);
n = unique(a, a + n) - a;
int ans = 0;
for (int i = n - 1; i >= 0; i--)
ans += (a[i] - ans * r > 0);
printf("%d\n", ans);
}
int main() {
int q;
scanf("%d", &q);
forn(i, q) solve();
}
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define x first
#define y second
const int INF = int(1e9);
int h, n;
vector<int> p;
inline bool read() {
if(!(cin >> h >> n))
return false;
p.resize(n);
fore(i, 0, n)
cin >> p[i];
return true;
}
inline void solve() {
int ans = 0;
int lf = 0;
fore(i, 0, n) {
if (i > 0 && p[i - 1] > p[i] + 1) {
if (lf > 0)
ans += (i - lf) & 1;
else
ans += 1 - ((i - lf) & 1);
lf = i;
}
}
if (p[n - 1] > 1) {
if (lf != 0)
ans += (n - lf) & 1;
else
ans += 1 - ((n - lf) & 1);
}
cout << ans << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
int tc; cin >> tc;
while(tc--) {
read();
solve();
}
return 0;
}
Idea: Roms
Tutorial
Tutorial is loading...
Solution (Roms)
n = int(input())
s = input()
res = n * (n - 1) // 2
for x in range(2):
cur = 1
for i in range(1, n):
if s[i] == s[i - 1]:
cur += 1
else:
res -= cur - x
cur = 1
s = s[::-1]
print(res)
Idea: Roms
Tutorial
Tutorial is loading...
Solution (Roms)
#include <bits/stdc++.h>
using namespace std;
void upd(int &a, int b){
a = min(a, b);
}
const int N = 20;
const int M = (1 << N) + 55;
const int INF = int(1e9) + 100;
int a, n;
string s;
int cnt[N][N];
int d[M][N];
int dp[M];
int cntBit[M];
int minBit[M];
int main() {
cin >> n >> a >> s;
int B = (1 << a) - 1;
for(int i = 1; i < s.size(); ++i){
++cnt[s[i] - 'a'][s[i - 1] - 'a'];
++cnt[s[i - 1] - 'a'][s[i] - 'a'];
}
for(int i = 0; i < M; ++i)
dp[i] = INF;
dp[0] = 0;
for(int msk = 1; msk < M; ++msk){
cntBit[msk] = 1 + cntBit[msk & (msk - 1)];
for(int i = 0; i < N; ++i) if((msk >> i) & 1){
minBit[msk] = i;
break;
}
}
for(int msk = 1; msk < M; ++msk)
for(int i = 0; i < a; ++i){
int b = minBit[msk];
d[msk][i] = d[msk ^ (1 << b)][i] + cnt[i][b];
}
for(int msk = 0; msk < (1 << a); ++msk){
for(int i = 0; i < a; ++i){
if((msk >> i) & 1) continue;
//i -> x
int pos = cntBit[msk];
int nmsk = msk | (1 << i);
upd(dp[nmsk], dp[msk] + pos * (d[msk][i] - d[B ^ nmsk][i]));
}
}
cout << dp[B] << endl;
return 0;
}
Idea: Roms
Tutorial
Tutorial is loading...
Solution (Roms)
#include <bits/stdc++.h>
using namespace std;
const int N = int(3e5) + 99;
int n;
vector <int> g[N];
int d[N];
int dp[N][2];
void dfs(int v, int p){
vector <int> d1;
dp[v][1] = d[v] - 1;
for(auto to : g[v]){
if(to == p) continue;
dfs(to, v);
dp[v][0] = max(dp[v][0], dp[to][0]);
if(g[to].size() > 1){
d1.push_back(dp[to][1]);
dp[v][1] = max(dp[v][1], d[v] + dp[to][1] - 1);
}
}
sort(d1.rbegin(), d1.rend());
int x = d[v] + 1;
for(int i = 0; i < 2; ++i)
if(i < d1.size())
x += d1[i];
dp[v][0] = max(dp[v][0], x);
}
int main() {
int q;
scanf("%d", &q);
for(int qc = 0; qc < q; ++qc){
scanf("%d", &n);
for(int i = 0; i < n; ++i){
g[i].clear();
d[i] = 0;
dp[i][0] = dp[i][1] = 0;
}
for(int i = 0; i < n - 1; ++i){
int u, v;
scanf("%d %d", &u, &v);
--u, --v;
g[u].push_back(v), g[v].push_back(u);
}
if(n <= 2){
printf("%d\n", n);
continue;
}
for(int v = 0; v < n; ++v){
//d[v] = 1;
//for(auto to : g[v])
// d[v] += g[to].size() == 1;
d[v] = g[v].size();
}
int r = -1;
for(int v = 0; v < n; ++v)
if(g[v].size() != 1)
r = v;
dfs(r, r);
printf("%d\n", dp[r][0]);
}
return 0;
}
1238G - Adilbek and the Watering System
Idea: Neon
Tutorial
Tutorial is loading...
Solution (Ne0n25)
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define mp make_pair
#define forn(i, n) for (int i = 0; i < int(n); ++i)
typedef long long li;
typedef pair<int, int> pt;
const int N = 500 * 1000 + 13;
int n, m, c, c0;
pair<int, pt> a[N];
li solve() {
scanf("%d%d%d%d", &n, &m, &c, &c0);
forn(i, n) scanf("%d%d%d", &a[i].x, &a[i].y.x, &a[i].y.y);
a[n++] = mp(m, mp(0, 0));
sort(a, a + n);
int sum = c0;
map<int, int> q;
q[0] = c0;
li ans = 0;
forn(i, n) {
int x = a[i].x;
int cnt = a[i].y.x;
int cost = a[i].y.y;
int dist = x - (i ? a[i - 1].x : 0);
while (!q.empty() && dist > 0) {
int can = min(q.begin()->y, dist);
ans += q.begin()->x * 1ll * can;
sum -= can;
dist -= can;
q.begin()->y -= can;
if (q.begin()->y == 0) q.erase(q.begin());
}
if (dist > 0)
return -1;
int add = min(c - sum, cnt);
sum += add;
while (add < cnt && !q.empty() && q.rbegin()->x > cost) {
if (cnt - add >= q.rbegin()->y) {
add += q.rbegin()->y;
q.erase(--q.end());
} else {
q.rbegin()->y -= cnt - add;
add = cnt;
}
}
q[cost] += add;
}
return ans;
}
int main() {
int q;
scanf("%d", &q);
forn(i, q) printf("%lld\n", solve());
}










typo in D. (n-1)*n/2
No that's not typo .Total count of possible substrings is n*(n+1)/2 (including substring of length one)
No, god. Please, no. No!!!
See , substrings of length 1 are bad , so they will be automatically counted in cntBad .So n(n+1)/2 is count of all substrings and cntBad = number of bad substrings .Hence n(n+1)/2 — cntBad is number of good substrings .For example consider "AAA" , here n(n+1)/2 = 6 and number of bad substrings i.e cntBad = 3 (Three substrings "A" of length 1 ) , thus total number of good substrings is 6 — 3 = 3 i.e the number we get after removing bad substrings from all possible strings .
We ignore them in the beginning, check the author’s solution.
If we take total substring as n*(n+1)/2 then we have to initialize cntBad = n at first.
And if we take total substring as n*(n-1)/2 then we have to initialize cntBad = 0. Authors solution took cntBad = 0.
So both are right.
Problem A Challenge: Assume, that you can substract a prime from x at most 3 times.
The solution is the same as to the original problem, because of Goldbach's conjecture (https://en.wikipedia.org/wiki/Goldbach%27s_conjecture).
I couldn't understand the explanation of problem C. Can someone describe it?
For explanation I'm using a test case:
9 8 5 4 3 1
Do you know what does this mean? Let me explain. It means that the height of the cliff is 9. So initially at 9, there is a platform where the player is standing. At height 8 there is a platform too. But at height 7 and 6 there is no platform by now. And then at height 5 and 4 and 3 there we have platforms at a stretch. Height 2 have no platform. Height 1 has platform.
At first you are at the highest point means at 9. From here we'll will see three kinds of moves. Let's see those:
Case 1: Do both of the next two height have platforms? If yes, then we can and should move to the second using 0 crystal.
Case 2: Do the next height have a platform? if yes, then it is optimal to move to that next height using 1 crystal.
Case 3: Now it means that there is at least one gap between now and the next platform. It doesn't matter if there is one or multiple gap. You can move to the very last gap using no crystal that means 0 crystal.
Now solve our test case: 9 8 5 4 3 1.
We are now at 9. Here we see case 2 because only the next height 8 has a platform. So we move to 8 using 1 crystal.
So now we are at 8. Here we see case 3 because we have gap at heights 7 and 6. So we move to 6 using 0 crystal.
So now we are at 6. Here we see case 1 because both of the next two heights 5 and 4 contains platform. so we move to height 4 using 0 crystal.
So now we are at 4. Here we see case 2. So we move to height 3 using 1 crystal.
So now we are at 3. Here we see case 3. So we move to height 2 using 0 crystal.
Now notice one thing. At Ground that means at height 0 we can assume that there is always a platform but it doesn't move at all. Because it's ground :D
So now we are at 2. Here we see case 1. So we move to ground using 0 crystal. So in total 2 crystal is used.
We need a crystal only when we meet case 2.
I hope you understand.
Hey MubtasimShahriar! Could you please explain me the output of : 100 1
Move from 100 to 2 using no crystal at all. From 2 you can move to ground that means to level 0 using 0 crystal. No crystal is used at all.
I don't understand that why are you going to 8 from 9 and not on 7, I mean we can use a crystal to change the state at height at 7 and then use a normal operation, I UNDERSTAND THAT YOU WROTE IT LONG TIME AGO, BUT PLEASE TRY TO EXPLAIN
Your's is fine too. In both way you have to spend a crystal to move to 7
In problem D is tagged as DP .Can some one tell the method to solve it using DP ? We can calculate bad strings using 4 different for loops (corresponding to type of bad string) , any other method to do that with less typing ?
For problem D, how can there be only 4 patterns? For example the string $$$ABBAB$$$ is also a bad string but its pattern is not the same as the 4 given patterns.
ABBA...BAB=> string is good
Oh thanks. I didn't read the question carefully, my bad.
Constraints are really deceiving in E. Could somebody explain an O($$$a*2^a$$$) solution?
The $$$a^2$$$ factor inside the dp is for computing the sums of $$$cnt_{x,y}$$$ for $$$x \in mask$$$ and $$$y \not\in mask$$$. You can improve this with sos dp, for each mask you compute how much should be added to.
The standard dp sos i'm thinking about is $$$a2^a$$$ for each character, which makes it $$$a^{2} 2^a$$$ in total. Could you explain further the recurrence of your dp?
I solved in $$$O(2^a * a^2)$$$ in the contest. I just coded the same ideia in $$$O(2^a * a)$$$ with sos dp.
If you calculate the cost in $$$DP$$$ by using the newly added letter's position:
Let $$$co[i][j]$$$ be the number of times letters $$$i$$$ and $$$j$$$ appeared next to each other. You can build an array $$$arr$$$ where $$$arr[i][mask]=\sum_{k\in mask} co[i][k]$$$ in $$$O(m*2^m)$$$, by using this trick: $$$arr[i][mask]=arr[i][mask\oplus 2^j] + co[i][j]$$$ for $$$mask>0$$$, where $$$j$$$ is any set bit's position in $$$mask$$$ (can be the lowest significant bit for example).
Got it. Thanks!
We can solve 1238E - Keyboard Purchase in O(m.2^m), too!
Denote dp[mask] as the minimum cost of arranging x's in mask on the keyboard when all of the y's not in mask are on the first key of the keyboard (all of them!). And denote sum[c][mask] as the number of positions that c and x's in mask are adjacent.
You can easily see that:
sum[c][mask] = sum[c][mask-lowbit(mask)] + sum[lowbit(mask)] (But you have to fill sum[c][2^x] before this by counting adjacent c's and x's in string)
and
dp[mask] = min(dp[mask-2^c])(for all c's in mask) + sum[x][2^m-mask-1](for all x's in mask).
Here is my code: 62207715
Thank you.
You're welcome! :)
But in my code I just used another for in calculating my dp every time I fix the c, so my code order is O(m^2.2^m), too! but you can easily change it.
In Problem D, I'm having trouble counting the number of such substrings. I read a lot of different codes but I don't seem to get it. Can somebody please explain their own method to me? Thanks a lot in advance.
let our string is AABBAAABAA here we have to find answer for AABB and BBAAA and AAAB and BAA. total of there will be answer for our string . And answer for string AAABB will be 3+2-1. We are subtracting 1 because we are adding the conjution (AB) twice . so answer for string AABBAAABAA will be (2+2-1)+(2+3-1)+(3+1-1)+(1+2-1)=12.
Helped a lot, thanks!
A proof for why the greedy algorithm works in $$$C$$$:
First note that for any $$$v>1$$$, you have to stand on at least $$$v$$$ or $$$v-1$$$, because if you didn't stand on both this means that you descended from $$$a>v$$$ to $$$b<v-1$$$, which means you are dead.
You are initially standing at $$$h$$$, assume you will walk without any crystals until you first reach that $$$x>2$$$ where $$$x-1$$$ is moved out and $$$x-2$$$ is hidden. Now you must use at least $$$1$$$ crystal to continue. You can use it either to:
The other scenario you can follow starting from $$$h$$$, is that which would end on $$$x-1$$$ (without going to $$$x$$$), and this scenario will cost at least $$$1$$$ crystal. So we deduce that the best option is option $$$2$$$ in the previous scenario. Starting from $$$x-1$$$, you can continue to use the same followed logic starting from $$$h$$$.
in problem E, when iterating to new character x then how we calculate dp[mask|(1<<x)] ?
I have tried an O(m^2*2^m) solution for problem E but it is giving TLE.
I cannot understand the solution of problem E. Specially, "If letter y is already on current keyboard, then we should add to answer cntx,y(posx−posy), and cntx,y(posy−posx) otherwise" sentence. Why should we consider the letter y which is not included in the keyboard? And on last formula,∑y∈msk(cntx,yposx)−∑y∉msk(cntx,yposx), why there is no posy? Where do they go?
Ah Sorry, I understand.
How do you erase cntx,y*posy? Can you explain? I think it is only possible when the two summations have the same range.
Maru can you please explain?,∑y∈msk(cntx,yposx)−∑y∉msk(cntx,yposx),
Can you explain why there is no posy??
Can any one explain how to solve D if there are 26 character?
Can someone explain how to solve D with 'binary search'?
How to solve D using DP?
Just a side fact: The resultant tree that gets formed in the problem F is also called Caterpillar Tree.
can someone please explain the structure of tree formed in problem F? I didn't get it from editorial completely.
It's a caterpillar: https://en.wikipedia.org/wiki/Caterpillar_tree
Thank you for your reply! But I am asking can you please explain how we land on this structure?
One major point here is that an integer can't be contained in three or more segments, since that would correspond to a cycle in the described graph, but we're given a tree, so that's ruled out. With this knowledge, let's construct some intervals so that we can maximise the number of intervals. We'll try to have two segments containing an integer as long as it is possible, since we're trying to maximise the size of the required subgraph.
So we have a continuous sequence of intersecting intervals, and then for points that are not yet covered by two intervals, we're trying to find as many non-intersecting intervals as possible to cover those points (you may even think of them as degenerate intervals, where l = r, if you want, since we're free to size our intervals as we please). The only thing that limits us is the given tree, where the smaller intervals can only be as many as the count of neighbours except the next interval in the path. I hope you see why this is optimal, and why this would correspond to the caterpillar graph.
Why is there a "Binary Search" Tag on Problem D? How to solve it using Binary Search?
How to understand the meaning of the dp array in E problem?
Problem fixed.
Sorry for inconvenience.
Read the statement carefully.When you will explosion on x=3 you will get 6 7 7 7
Then every monster is either killed by explosion or pushed away.
if you'll fire at c=3 then positions will become 6,7,7,7
awoo, in problem E, could you explain how you arrived at the final formula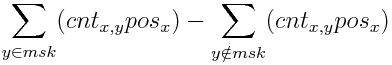
got it now..
can u explain it here plz
thnx . got it now
can you explain it again?
Can you please explain how this formula arrived !!
Can Someone Explain What d[M][N] represents and how we used it to calculate dp[M] in the editorial for problem E?
Can someone please share some way to actually count the number of good substrings(not negating bad substrings), just curious!!
Doubt in problem E.
Hi, i have a question about why my code didn't get TLE.
My idea:
Imagine the graph with letters as nodes and weighted edges (the weight of an edge is how many times the node u came right before node v or node v came right before node u in the string).
I used the fact that |a-b| = max( a,b ) — min( a,b ).
So i started selecting the letter (or node) with the position $$$N$$$, the the letter with position $$$N-1$$$ and so on, obviously taking care not using a node twice. And with this in mind a node $$$u$$$ will add (its postion) times (the sum of the edges from that node to the rest of the nodes that have not been selected yet) — (its position) times (the sum of the edges from that node to the rest of the nodes that have been selected ).
I did this but i think that the complexity is m^3 * 2^m which is somethig like 8*10^9 worst case.
Could someone explain me why this solution passed?
My code: 62655475
In problem D, what is the role of x in res-=cur-x. For the first iteration of the loop we check for strings that end with AAB or BBA. And for the second iteration we check for strings that start with ABB or BBA. Why subtract x=1 from res ? Got it.
can you tell me why?? i am looking for such a comment.
Can someone please explain the intuition behind problem E and can anyone please give some tips to improve bitmasking.
Random solution to problem F gives ACC, is it because test cases are weak? 63616653 I just choose 20 nodes at random plus the center(s) of the tree, and for each of them run the same dfs assuming that answer pass through it. Can someone tell the probability of choosing a vertex and it belongs to an answer? I know it's something like ANSWER / N.
Suppose we have a tree with $$$\sqrt n$$$ branches of length roughly $$$\sqrt n$$$, where two of the branches are a bit longer. Then, the answer contains roughly $$$3\sqrt n$$$ vertices, so the probability of choosing a node that is part of the best subgraph is roughly $$$3 \sqrt n / n \approx 0.005$$$ for $$$n=3\times10^5$$$. If you choose 20 nodes at random, then the probability of failure is roughly $$$0.995^{20} \approx 0.89$$$, so this solution shouldn't pass.
would someone plz answer my question ??
In problem B, tutorial's time complexity is O(n * logn) in every query. so i think total time complexity of the algorithm is O(q * n * logn).
https://codeforces.com/contest/1238/submission/64450447 — this is my code. my time complexity is O(n+log n) ~ O(n) in every query. so i think total time complexity of my algorithm is O(q*n).
my question is why the tutorial's code passed but mine couldn't passed?
Your complexity is O(q*MAX) where MAX=1e5.
Oh, Thank you! i understand that
wait, in problem B if the complexity in each query is O(n log n) then does that mean the whole problem will be O(q*n*logn), how does this still work with q <= 1e5?
Read the constraints. It is clearly written — "It is guaranteed that sum of all n over all queries does not exceed 10^5.". Thus the time complexity is O(q*n*logn) but q*n<=1e5.
Can anyone tell me why am i getting TLE in B ?
Do read the blog first .
Because the reason behind TLE is strange link to the blog is here...
Constraints on E is unecessarily too tight, usage of long long gives TLE
Educational Forces = Diagonal Pattern,chess pattern,snake pattern or some random string pattern