This algorithm can solve some difficult data structure problems. Like this: Give an array a[] of size N, we query Q times. Each time we want to get the mode number(the value that appears most often in a set of data) of subsequence a[l], a[l + 1] .. a[r].
Maybe you want to solve it by segment tree or some other data structures. However, if you know the answer of [l, middle], [middle + 1, r], it's difficult to get the answer of [l, r].
Here is an offline algorithm which can solve this problem in O(N * sqrt(N) * log(N) + Q log Q).
First we need a data structure that can support: insert a number. delete a number. get the mode number. It can be solved easily by binary heap / balanced binary search tree. We call this data structure DS.
Secondly, if we have all the numbers in [l, r] organized in DS, we can transform to [l', r'] in O((|l-l'| + |r-r'|) * log N). We need a good tranform order.
S = the max integer number which is less than sqrt(N);
bool cmp(Query A, Query B)
{
if (A.l / S != B.l / S) return A.l / S < B.l / S;
return A.r > B.r
}
We sort all the queries by this comparator, and it can be proofed easily that the total transform costs is N sqrt(N) log N.










Thanks in advance.
....So why does this post keep getting negative feedback...
EDIT : Now it starts to get positive votes
I think, that it's just nice usage of SQRT-decomposition idea, but not algo that deserves to be named in honor of person.
I'm so sorry but this algorithm is famous as Mo's algorithm in Chinese high school student. Here I just use the ordinary name.
How can this problem be solved with less time complexity?
is there any problems in oj?
I was told the similar solution to this problem 86D - Powerful array
i liked it "86D — Powerful array"
I got a couple of questions: - Which value would S take if there wasn't any element having a value less than sqrt(N)? - Could you please describe the proof of the overall time complexity? EDIT: When you say the max integer which is less than sqrt(N) you mean floor(sqrt(N)), then it makes sense and the proof is easy as you already said, sorry for the misunderstading.
Why A.r > B.r? I can't see it, shouldn't it be < instead?
Both them are right. let l' = l / S For all the queries whose l' is the same, the movement of right pointer is monotonous, so the total costs is O(N). And there can be at most S kinds of queries whose l' is different, here S = sqrt(N), so the total costs of right pointer movement is at most N * sqrt(N)
Yeah i just realized that it doesn't matter on my way back to home. Thanks for the reply.
thanks for good algorithm.
I think it can be solved in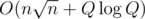 .
.
A.r < B.rin the last line.cnt[]wherecnt[x]is how many times number x was met. Also we will maintain the numbermaxNumwhich was met maximal number of times (cnt[maxNum]is this number of times).A.l == B.l. So there arecnt, then...r = k*S(k = 1, 2, ...) (it's the first element of the next block in sqrt-decomposition) and move it to the right, updatingcntandmaxNum. If some query in this block has the right border equal tor, then...maxNumin the temp variable and move pointerlfrom positionk*Sto the left while it is not equal to current query's left border. It will move to distance no more thancntand variablemaxNumduring this process.lis equal to the query's left border we can answer the query — it ismaxNum. Then move pointerlback to the right, to its initial placek*S, updatingcntwith subtractions, not additions. Finally, variablemaxNum— the most appearing number — is now wrong — we cannot maintain it when we subtract fromcnt. But we stored its actual value (for segment [kS, r]) at the beginning of step 5. Our data structure became consistent and we can continue processing the queries.Какого размера массив cnt ? макс-ое значение среди элементов? Это просто замена map на vector ?
Думаю лучше прочесть решение ниже.
Here is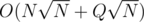 idea.
idea.
First of all, lets sort all queries using your comparator.
Let array S[N] be an array, which consist of N hashsets. S[i] contains all numbers, which appear in our current segment exactly i times. Let A[n] be an array(or hashmap), where A[i] contains the number of appearances of number i in our current segment. Let max be the biggest index of nonempty set in S
Using this structures, we can add or delete number in O(1) time:
1) Add some number v: delete v from S[A[v]], increase A[v] by 1, add v to S[A[v]], if A[v] > max — increase max by 1.
2) Delete some number v: delete v from S[A[v]], decrease A[v] by 1, add v to S[A[v]], if S[max].size() = = 0 — decrease max by 1.
To get answer for the query we just take any number from S[max]
Since S[i] is storing numbers, won't it take O(logN) time for each add/delete operation and that too when we use some container like set. Otherwise delete operation could take O(N) time. Please correct me if I'm wrong.
Although we can solve this question if instead of storing numbers that appear exactly i times, we store the count of such numbers in S[i], I found this technique really useful.Edit: Thought we just need to output the mode number's count. Thanks!The total transformation cost is (N sqrt(N) + Q sqrt(N) )log N instead of N sqrt(N) log N, because for each query in the worst case you will have to go through a whole block of length sqrt(N).
There's one cool adaption of that: Say you have a data structure that supports
inserttrivially but notdelete. There are lots of examples where this is the case.Assume however that we can implement a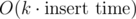 , where k is the number of inserts since the snapshot. Every persistent data structure makes this possible trivially, but that's actually more than we need and often we can find tricks to implement these operations in a much simpler way, possibly even by using
, where k is the number of inserts since the snapshot. Every persistent data structure makes this possible trivially, but that's actually more than we need and often we can find tricks to implement these operations in a much simpler way, possibly even by using
snapshot()androllback()function for our data structure, so that arollback()brings us back to the state of the latest snapshot inmemcpyWe can still use the technique presented here with runtime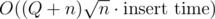 .
. 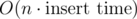 .
.
init()can have complexityIn the following code, we assume zero-based indexing of the queries and inclusive right borders:
Will you please elaborate a bit? Will you do rollback, if you need O(n) or O(nlgn) to do it?
You do that Ω(Q) times, so to stay within the time bound, we have to be able to charge it the inserts that happened since the last snapshot. That's why I said it must be bounded by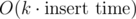
Now that the contest is finally over, would you mind answering why you posted the solution to this problem while the contest was midway?
Someone asked a question about the problem on Stack Overflow (obviously without reference to the source). I came up the idea (or better reinvented it, since it seems to be quite well-known), and because it seems like a generally useful construction I posted it here. When I was notified by a fellow user that it is from a running contest, I removed the references to DSU, which seems to be the core idea, but well you can always see the old revisions. As you might know, there is no option to delete your posts on Codeforces.
Unfortunately it often happens that we get questions about running contests on Stack Overflow. It is not against SO's rules to post them there, so they cannot be deleted and often get good answers as well. I have seen at least 20 questions about the MIKE3 and SSTORY problem, some had good answers, and I have also unknowingly described a solution for STREETTA there towards the beginning of the contest. Even if you realize this later, you cannot delete your answers once they are marked as accepted. After you see the same question 3 times in a row you can usually figure that something is probably up, but then it's often too late. What can I say. Just one more reason to have more fellow competitive programmers on Stack Overflow to spot these types of questions and mark them in the comments.
The same goes for cs.stackexchange.com I suppose, although it is a bit less frequented.
I guess in the end this is all about fun, so whoever used this approach blindly without thinking about it further has missed a good opportunity to come up with the much more elegant approach using Link-cut trees... It will probably haunt you in the future :)
What surprised me initially was that you had submissions to the problems of this contest before you posted this solution. Now I see that all the initial submissions were to the problem ANUGCD, so I assume you only had that one problem read at the time of this post.
Yes indeed, the reason I looked at ANUGCD was yet another Stack Overflow post that made me interested in that particular problem.
Hmm, you can always edit your answer, make it become blank for example!
And you can just look at the old revisions.
"First we need a data structure that can support: insert a number. delete a number. get the mode number. It can be solved easily by binary heap / balanced binary search tree."
Another easy way would be to keep a map of (number, frequency) and a set of pair (frequency,number). Insertion/Deletion are O(log N). Getting mode is O(1).
Thanks for sharing.It's really helpful for me to learn Mo's algorithm. I can hardly find a paper about Mo's algorithm on Internet.
I found this article, seems to be more detailed: https://www.hackerearth.com/notes/mos-algorithm/
Thanks!
here is another one with clean discussion http://blog.anudeep2011.com/mos-algorithm/
It seems that this cmp is faster than your cmp:
2182 MS with above cmp: 15551689
3586 MS with your cmp: 15558775
This is very specific on tests. I'm pretty sure that tests in this specific task are bad enough to be optimized nearly twice this way.Your comparator is completely identical to the one presented in this blog if all queries are in the same bucket of size S.UPD: one can prove that this comparator is better like this
Your cmp is for <= operator. So it can gain RE.
Yes. You're right. Use this function instead:
It is too awesome. My TLE converted to Accepted by just changing Mo comparator But may I know why? What is the reason behind the efficiency of this comparator?
Visualize it.
Oh nice, It was amazing, Please tell me if I am right that while right pointer is returning back towards the block for queries in odd block then changing sorting order in even block (every time direction changes for right pointer) helps to solve the query in next block while going away from even block (towards right). thus reducing significant amount of left to right iterations for right pointer and instead using left to right movement and right to left movement of right pointer effectively.
Yes.
If we had all queries with l in the same segment, except that in sorted order they alternate with one starting at the beginning of the segment, the next starting at the end of the segment. Wouldn't the time complexity for queries be O(Q log Q + Q * sqrt N)?
By segment I mean the sqrt N partition.
what is mos algo + dp my sol is not passing in 2 sec by only mo's algorithm where both n and q is 5e5
I think you are asking for this HackerEarths Happy Segments ? Happy Segments
how to sort like this in python?