Друзья, вот и закончился онлайн-тур ABBYY Cup 3.0!
Спасибо большое всем участникам! Мы приносим свои извинения за проблемы с тестированием. MikeMirzayanov всех уже обрадовал планами о закупке тестирующих машин. Надеемся, что в будущем таких ситуаций не повторится.
А вот и разборы задач:
Это была одна из самых простых задач из предложенных. Решение задачи сводится к рассмотрению нескольких случаев. Изначально ответ равен единице. Заметим, что если в строке встречается "?", то он увеличивает число возможных кодов в 10 раз. За исключением случая, когда "?" стоит в начале строки. Тогда он увеличивает число возможных кодов в 9 раз. Далее нужно рассмотреть случаи, когда среди символов строки встречаются буквы. Тут нужно рассмотреть два случая:
Заметим, что в данной задаче необязательно реализовывать длинную арифметику. Так как все операции за исключением умножения на 10 из-за "?" можно выполнять с помощью стандартной арифметики. А для умножения на 10 можно просто вывести в ответ нужное количество нулей.
Заметим, что понятие порядка мячей соответствует перестановке, а ограничение на число бросков для ученика соответствует ограничению на число транспозиций. Нужно посчитать число “подходящих” перестановок. Заметим, что если перестановку разбить на циклы, и в каждом цикле будет не более двух элементов с максимальным числом инверсий равным 1, то рассматриваемая перестановка является “подходящей”. Таким образом, задачу можно решить с помощью динамического программирования. Нужно вычислять функцию f(a, b), где a – число 1, а b – число 2, которые мы использовали. f(a, b) – число “подходящих” перестановок. Заметим, что данную функцию можно вычислять с помощью следующей формулы: 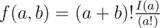 , где I(n) = I(n - 1) + (n - 1) * I(n - 2)) Ее доказательство оставляем читателям в качестве упражнения.
, где I(n) = I(n - 1) + (n - 1) * I(n - 2)) Ее доказательство оставляем читателям в качестве упражнения.
Данная задача имеет множество решений. Рассмотри одно из них. Обозначим исходное изображение за T. Будем применять к T две операции: эрозия и дилатация. Операция эрозии – замена всех пикселей, которые относятся к изображению и граничат с пикселями фона, на пиксели фона. Дилатация – это в некотором смысле обратная операция, мы заменяем пиксели фона, которые граничат с пикселями изображения, на пиксели изображения. Заметим, что для определения соседних пикселей лучше использовать 4-связность. Итак, мы применяем к исходному изображению несколько операций эрозии. После этого лучи исчезнут и останутся только центры солнышек. Далее применяем несколько операций дилатации. Заметим, что число операций дилатации должно быть больше, чем операций эрозии. Обозначим полученное изображение за P. Далее рассматриваем исходное изображение T и выделяем в нем компоненты связности, соответствующие солнышкам. Далее из каждой такой компоненты необходимо выделить части, соответствующие лучикам. Лучикам соответствуют, в свою очередь, Пиксели изображения, которые есть на изображении T, и которых нет на изображении $P.
Первое, что нужно сделать в данной задаче – это выделить цепочки в заданной очереди. Цепочка – это последовательность бобров, которые стоят в очереди непосредственно друг за другом. Таким образом, мы получим все длины цепочек и цепочку с Умным Бобром. И далее требуется просто применить стандартное ДП для вычисления возможных сумм.
Перейдем от исходной матрицы к двухдольному графу. Элементы матрицы (i, j) с четными значениями i + j поместим в одну долю, а с нечетными — в другую. Ребра будут соответствовать квадратам, которые находятся рядом. Далее добавим веса для ребер. Ребра, соединяющие одинаковые элементы матрицы, будут иметь вес 0, соединяющие разные — вес 1. После этого в полученном графе нужно будет найти максимальное паросочетание минимального веса. Его вес будет ответом к задаче. Обоснование вышеизложенного заключается в том, что любой ответ для задачи будет представлять собой некоторое разбиение исходной матрицы на пары. Заметим, что для некоторого разбиения минимальное число элементов матрицы, которые изменятся, будет соответствовать числу пар, в которых числа различаются. Таким образом, оптимальным будет то разбиение на пары, в котором число пар одинаковых элементов будет максимальным. Заметим также, что для построения максимального потока минимальной стоимости требовалось использовать какой-нибудь эффективный алгоритм. Например, можно было использовать алгоритм Дейкстры с кучей вместе с преобразованием весов ребер алгоритма Джонсона.
Для решения данной задачи будем использовать дерево отрезков. Рассмотрим некоторый отрезок [l;r] на этом дереве. Для него введем функцию S(x), где x – целое число. S(x) = F0 + xAl + F1 + xAl + 1 + … + Fr - l + xAr, где Fi – i-е число Фибоначчи, Ai – рассматриваемый массив целых чисел. Заметим, что S(x), для x = 0, 1, 2…, представляет собой некий аналог чисел Фибоначчи. То есть S(x) = S(x - 1) + S(x - 2), для x≥2. Из этого следует, что нам для каждого отрезка [l;r] нужно хранить только S(0) и S(1). А для вычисления S(x) для x≥2можно пользоваться следующей формулой: S(x) = S(0)Fx - 2 + S(1) * Fx - 1. Итого, разрешение запросов 2-го типа сводится к вычислению не более чем 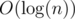 значений S(x) для различных отрезков. Модификации 1-го типа выполняются тривиальным проходом по дереву. Для запросов 3-го типа нужно использовать дополнительную информацию в дереве и частичные суммы чисел Фибоначчи.
значений S(x) для различных отрезков. Модификации 1-го типа выполняются тривиальным проходом по дереву. Для запросов 3-го типа нужно использовать дополнительную информацию в дереве и частичные суммы чисел Фибоначчи.
Для начала нужно научиться быстро сравнивать две любые подстроки, которые можно взять из исходной строки или из одной из строк, соответствующей правилам. Это можно сделать, например, с помощью построения суффиксного массива, содержащего все строки ввода. После построения такого массива и вычисления значений LCP задача сравнения двух подстрок сводится к вычислению числа одинаковых символов и сравнении символов, которые идут после одинаковых блоков. Вычисление числа одинаковых символов эквивалентно задаче вычисления минимума на интервале массива значений LCP. Так как массив LCP не меняется, то эффективное разрешение таких запросов можно делать с помощью RMQ-алгоритмов. Таким образом, мы можем за O(1) сравнивать две любые подстроки. Заметим, что время препроцесса зависит от используемых алгоритмов для построения суффиксного массива и построения RMQ.
Далее нам нужно научиться находить число вхождений некоторой подстроки исходной строки в строку одного из правил. Это можно делать с помощью бинарного поиска по суффиксному массиву строки правила. Заметим, что мы можем сравнивать две подстроки за время O(1). Поэтому сложность поиска числа вхождений подстроки в строку будет 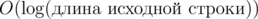 . Теперь рассмотрим некоторый суффикс исходной строки. Мы знаем его LCP с предыдущим суффиксом. Это будет нижняя граница на длину этого суффикса. Заметим, что число вхождений некоторого префикса рассматриваемого суффикса монотонно зависит от длины этого префикса. Поэтому, для каждого правила можно бинарным поиском определить, какой может быть минимальная и максимальная длина префикса, чтобы он подходил под правило. После чего необходимо просто пересечь все полученные интервалы.
. Теперь рассмотрим некоторый суффикс исходной строки. Мы знаем его LCP с предыдущим суффиксом. Это будет нижняя граница на длину этого суффикса. Заметим, что число вхождений некоторого префикса рассматриваемого суффикса монотонно зависит от длины этого префикса. Поэтому, для каждого правила можно бинарным поиском определить, какой может быть минимальная и максимальная длина префикса, чтобы он подходил под правило. После чего необходимо просто пересечь все полученные интервалы.
Возможно, что с использованием других структур данных на строках можно получить более простое решение. Техническая реализация рассматриваемого решения является довольно трудоемкой.











Благодарю! Контест был очень интересным!
Вот я кстати совершенно не понимаю, зачем в С требовать "эффективного" минкоста? Во-первых, у некоторых людей зашел простой минкост(у меня, например), во-вторых, идейная сложность этой задачи именно додуматься до минкоста. Зачем это было сделано?
Поздравляю! А почему ты не соревновал через почти целый год?
Множество различных факторов, которые наложились друг на друга. Постараюсь таких длительных пауз в ближайшее время не делать.
The problems were interesting enough! Thank you!
Можно подробнее про стандартное ДП в ЭКГ?
Рюкзак: длины цепочек -- это веса предметов. Каждый предмет можно использовать только один раз, стоимостей нет. dp[i][j]=true, если и только если можно набрать вес i с помощью первых j предметов
спасибо. Наконец-то решил))
First, consider the case that all people can only throw one time. Let's define the number of this cases of n people is I(n). The nth people have two possible ways to make loop.
(1) He himself is a group. The number of this case equals I(n-1), because he has nothing to do with other people.
(2) He and another one form a group. There are n-1 ways to choose another people, then these two person have nothing to do with others, so the number of this case (n-1) * I(n-2) So, I(n) = I(n-1) + (n-1) * I(n-2)
Now Consider the case that there're some people can throw twice, there's no limitation to these people, so they can insert to any loop's any position. If a loop has n people, then there're n positions can be inserted. So the number of all positions is the number of people. And an addition is he doesn't insert to any loop but to form a new loop.
Assume there're n people can throw only once, m people can throw twice, so the answer is (n + 1) * (n + 1 + 1) ... *(n + m — 1 + 1) * I(n) = I(n) * (n + m)! / n!
What does "loop" mean here?
Assume there're 5 people ,consider the permutation [2, 1, 4, 5, 3].
The first people's ball go to the second people.
The second people's ball go to the first people .
The third people's ball go to the fifth people.
...
We can use a directed graph to describe the case: (please forgive my baoman style)
And there're two loops in this permutation —— [1,2] [5,3,4]
To insert a people to a loop, just break one edge and add two new edges.
The limitation is only that a loop contains at most two people that can throw ball once, so the people who can throw twice can be inserted to any position.
AWESOME EXPLANATION! Thank you.
But How could the insert operation work?
please, upload these images to photohosting and give our the links only.
It's really huge :)
I completely know I(n) through your excellent explanation.But if you can explain the proof of l(n)*(n+m)!/n! in detail,I would be very grateful.
Ее доказательство оставляем читателям в качестве упражнения.я нашёл поистине удивительное доказательство этого предположения, но поля здесь слишком узки для того, чтобы вместить его.
Думаю, что тут должно быть так:
S(x)=F0 + xAl + F1 + xAl + 1 + ... + Fr - l + xAr
нет, имелось в виду
F0 + xAl + F1 + xAl + 1 + ... + Fr - l + xAr. Но догадаться до этого можно только с большим трудом.
А мне набор задач не очень понравился.
A, B, D — замечательные.
F — лично мне такое нравится, но вообще на отборочный тур давать задачу с плохо формализованными входными данными — совсем не комильфо. Вот на нерейтинговый контест, для интереса, — пожалуйста!
C — фейл с выбором органичений, а если забыть про этот фейл, то это просто упражнение на тему «паросочетания/потоки».
E, G — сугубо профессионализм; не люблю такое в олимпиадном программировании. У кого готов преднаписанный код, тот и победил.
Спасибо за работу, впрочем, — в любом случае.
Ну, в Е все-таки скорее догадаться. Дерево интервалов нынче у всех в пальцах уже. В F можно немножко дописать, чтобы ограничения стали формальными. Но они были настолько слабыми, что проходило все что угодно
Не знаю, на 70 баллов проходит вот это и вот это соответственно. ИМХО, профессионализмом тут и не пахнет.
Дерево Фенвика и z-функция? Спасибо, что идеально проиллюстрировали мой же тезис! :)
Их же знают только олимпиадные программисты, и выучили их ровно с одной целью — чтобы олимпиадно программировать на соревнованях по олимпиадному программированию! :-)
«Вот за это нас, олимпиадных программистов, и не любят» :)
Миша, вот от тебя не ожидал такого про z функцию услышать. Ты же знаешь, откуда у нее ноги растут?
То, что есть области, где и то, и то в принципе применяется, я не спорю.
Но то, что сложилось сообщество, где принято соответствующий код знать наизусть, — мне кажется довольно странным.
Ну, сейчас уже, соответственно не наизусть, а на-e-maxx :-)
Всё равно странное наше сообщество, и то, что люди продолжают придумывать задачи «а вот ещё такой подвыподверт с z-функцией» и «хм, а вот по такому ключу дерево отрезков мы ещё не реализовывали», это во многом «вещь в себе».
It seems that S(x) = F0 + xAl + F1 + xAl + 1 + … + Fr - l + xAr must be S(x) = F0 + x × Al + F1 + x × Al + 1 + ... + Fr - l + x × Ar in the solution of "Summer Homework". And there are more typos because it uses Fx + 1 instead of Fx + 1.
any hints on why S(x) = S(0)Fx-2 + S(1)Fx-1?
This formula holds for all fibonacci-formed sequence a0, a1, a2, ..., an. We can prove this by induction.
The inconvenience caused with the testing part was really frustrating. There was a time when I accidentally submitted a C solution while I had selected python, and I got to know after half an hour the mistake. Caused me a lot of rank loss. Anyways, nice problems and fast editorials.
Your graph is smooth...
my submission no. 3872882 was judged correct during the contest but after the contest it was judged as skipped can u check into the matter . i am losing 30 points because of that.
Probably, because of cheating with source code. If you write code on your own — contact administration and ask them to solve this issue.
good job Kenny
Because of that:3871903, 3872882
It's always funny to see how cheaters complain.
I am wondering how you found these two submissions.
He has wrote his submission number, and another i've found here: http://codeforces.com/contest/316/status , using filter.
good job
Может, убрать разбор с главной? А то захочет кто-нибудь сам порешать, заходит на сайт, а ему сразу же разбор.
" И далее требуется просто применить стандартное ДП для вычисления возможных сумм." задача В. Не совсем понял как.
Выше fetetriste рассказал подробно.
После отработки алгоритма в массиве
возможные_суммыбудут стоятьtrueтам, где можно достичь эту сумму. То есть основная идея в том, что индекс массива — это возможная набранная сумма.Ясно. Спасибо.
Suffix Automation is a good way to solve Prblem "Good substrings".It is very easy to implement and the code is short!
Hi,
Somebody could explain for me the "Tidying up" problem? :) I read this editorial and check some of solutions (e.g. 3873637 it is nice clean solution), but I don't see why this flow problem is equivalent with the original problem. Thank you..
Well, let's notice an obvious fact that if we want to put a pair of shoes into two adjacent squares, it's never efficient to remove both old shoes and replace them with two new ones. So, we build a bipartite graph, in which we need to find a perfect matching (an edge taken into matching means that we've put a pair of shoes into this pair of adjacent squares). So, 0-weighted edges mean that we just leave both shoes on their original place, and 1-weighted edges mean that we remove one shoe (and replace it with another).
Thank you for your answer! Why this is obvious fact? What is the mathematical explanation?
Why do you make me think instead of you? :)
Let's consider some facts.
Let's prove statement 4. Let's consider edges from matching as pairs (a[i], a[i + 1]). Since we have exactly two shoes of each type, these pairs can be split into cycles of the following form: (a[1], a[2]), (a[2], a[3]), ..., (a[n — 1], a[n]), (a[n], a[1]). So, you can fix either the first element of each pair, or the second one, and move the remaining element. So, for each edge from matching that connects shoes of different types, we need to move exactly one shoe. Q.E.D.
Well, I want to say (even 4 years have passed), the algorithm of the problem "Tidying up" is not completely correct. Try this data: N=2, M=8, and the tab is: 3 1 3 2 1 2 4 4 5 5 6 6 7 7 8 8 In the case above, the answer should be 2, obviously. But most of the programs that got "Accepted" during the competition printed 3. (Maybe I am wrong because of my poor English reading QwQ) I am not good at English, so maybe the text above is meaningless... I hope you can understand what I mean, Sorry.
А сейчас где-то можно достать тесты из условия к задачам F1-F3? Ссылка внизу условия на sun.zip не работает
Can anybody plz explain why my solution gets RTE when i used long long int but gets AC when i used int data type...? i submitted same solution in different versions of C++ language... it's not the first time i faced this kind of problem... my solution link--> https://codeforces.com/contest/316/my