tl;dr — video tutorial https://www.youtube.com/watch?v=eMXNWcbw75E and codeforces GYM training https://codeforces.com/gym/102644 (register by finding this contest in GYM instead of using the link directly)
video editorial: part 1 (ABCDEF) and part 2 (GHI)
codes to all 9 problems: https://github.com/Errichto/youtube/tree/master/matrix-exponentiation
Prerequisites: binary exponentiation and iterative dp (you don't need to know matrices)
The youtube tutorial (link) focuses on intuition and graph-like visualization . Or, if you prefer, below is a shorter (less detailed) text tutorial instead. You can practice by solving a set of 9 educational problems in GYM https://codeforces.com/gym/102644. ABCD are easy, EF medium, GHI are hard. If you are stuck, see hints below or watch the full solution analysis — part 1 (ABCDEF) and part 2 (GHI).
Hints
Matrix Exponentiation
Consider this problem:
String Mood — Limak can be either happy or sad. His mood changes (or stays same) when he reads an English uppercase letter. Letters S and D always make him sad, H makes him happy, and every vowel (AEIOU) flips his mood. Other letters do nothing.
Limak is happy right now. Among all $$$26^n$$$ possible strings of length $$$n$$$ ($$$n \leq 10^{18}$$$), count such strings that Limak will be happy after reading that string, modulo $$$10^9+7$$$.
If something can be solved with dp in $$$O(1)$$$ space, we can usually speed it up later with matrix exponentiation. This dp is easy — for length from $$$1$$$ to $$$n$$$ compute the number of strings making you happy and making you sad at the end.
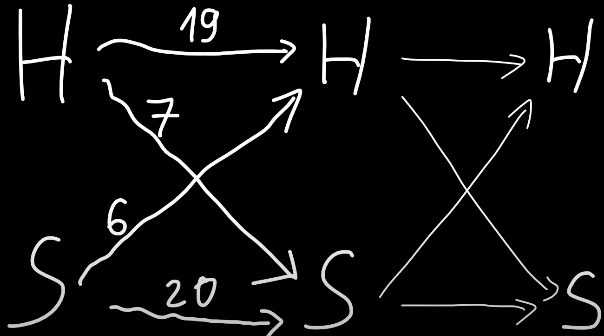
Let's visualize that by drawing vertices representing the two moods, and edges with the number of ways to move from one state to the other.
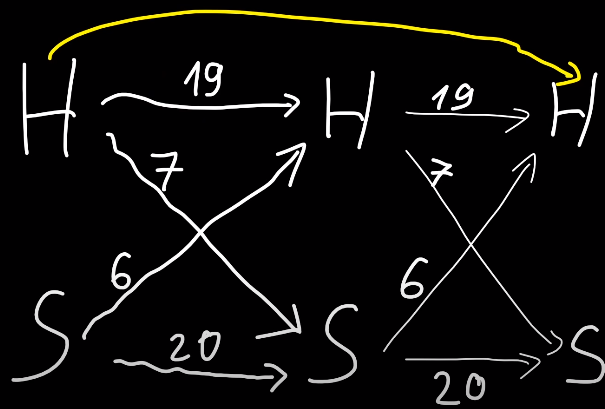
For example, if you are happy, there are 19 ways to make you happy and 7 ways to make you sad (SDAEIOU). Thin edges on the right represent the second letter of a string and the number there should be the same, because they are again 19 ways to make you happy if you were happy, etc. If we were asked about answer for $$$n = 2$$$, we would need to compute the number of ways to get from HAPPY state in first column to HAPPY state in third column, which is they yellow edge below.
That's $$$19 \cdot 19 + 7 \cdot 6 = 403$$$. In a similar way, we can compute all four counts for 2-letter strings: happy to happy (equal to $$$403$$$), happy to sad ($$$19\cdot7+7\cdot20=273$$$), sad to happy ($$$234$$$), sad to sad ($$$442$$$). We'll actually keep these four values $$$ [ [403,273], [234, 442] ] $$$ in a 2-dimensional array, also called a matrix.
Starting from a matrix with four values describing 1-letter strings $$$[ [19,7],[6,20] ]$$$, in $$$O(1)$$$ we got a matrix describing 2-letter strings. We can do the same to get a matrix for 4-letter strings, then 8-letter strings, and so on. We can do binary exponentiation to find a matrix for any huge $$$n$$$. Formally, we compute $$$M^n$$$ where $$$M = [ [19,7],[6,20] ]$$$ and multiplying two matrices is exactly what we did above to compute a new matrix $$$[ [403,273],[234, 442] ]$$$, done with the following code:
for(int i = 0; i < s; i++) { // s is the number of states, s=2 in the String Mood problem
for(int j = 0; j < s; j++) {
for(int k = 0; k < s; k++) {
new_matrix[i][k] += matrix1[i][j] * matrix2[j][k];
}
}
}
The total time complexity is $$$O(s^3 \cdot \log n)$$$ where $$$s$$$ is the matrix size (also called order), which is equal to the number of states (variables) you need in space-efficient dp. We had $$$s=2$$$ in String Mood so the complexity is just $$$O(\log n)$$$.
Now, try to find the $$$n$$$-th Fibonacci number for $$$n \leq 10^{18}$$$ (problem link) by first implementing space-efficient dp with transitions of form new_variable += old_variable * x where $$$x$$$ is some number you will need to put in the initial matrix (like $$$19$$$ or $$$7$$$ in String Mood).
Footnote
Thanks to tnowak for suggesting and creating one problem, and to mnbvmar for a few problem ideas. For the future, I'm looking for somebody to help me with the preparation of such training contests. If you want to help and you are high-rated and perfectly with experience in using polygon, please write to me. I can pay you a little if you want.
I hope you learned something thanks to this tutorial. Feel free to discuss problems from the GYM contest or give links to more matrix exponentiation problems or useful resources. If anybody wants that, I can make tests public. If you are a teacher and want to use some problems in your classes, I will give you access in Polygon.











I assume there is no way to register lately for such contest? Unfortunatly there seems to be no way to submit without registering.
Apart from that, thanks for the work, I can submit after contests ends, too.
Strange, it should be possible. Maybe go to GYM tab and find the contest there?
Yes, from GYM tab registration works, thanks.
I think you should make group or something if you are willing to organise more such contests :)
"I can pay you a little if you want". Respect for this helping attitude of yours.
It's good that you are appreciating his effort but please never say pay you, it kind of sounds disrespectful for the effort he has Put in. These are some of the situations where person did not care about money but rather just want to help others.
Kind of a stupid concern, but why does WA on pretest 1 give a -1? If someone has a WA on pretest 1 and then AC, he gets +1 in standings.
Waiting for the video :>
Can anyone suggest where I am wrong at
I. Count Paths Qeuriesit is still givingTLEYou are still doing matrix-matrix multiplications when answering queries. That will be too slow. You need to do vector-matrix multiplications. I.e. if you want to compute
v*M*N*O*P, do(((v*M)*N)*O)*Pinstead ofv*((((N*M)*O)*P).But first, you need to work out the vector
v.(((v*M)*N)*O)*PI am doing this only , what make you think I am doingv*((((N*M)*O)*P)By the way thank you very much I got AC by vector-matrix multiplication.
v(or yourI) is a $$$n \times n$$$ matrix, and therefore each multiplication is $$$O(n^3)$$$. It needs to be a vector (so $$$1 \times n$$$). That way every multiplication is $$$O(n^2)$$$.Yes , I was able to score AC with your suggestions
The multiply() works in $$$O(n^3)$$$, right?
You call multiply q*log(k) times, which makes it $$$O(n^3 * q * log(k))$$$
Since q==n it is basically $$$O(n^4 * log(k))$$$
Jakube is correct that you should do vector-matrix multiplication. And you should compute the time complexity next time before asking why your code is too slow.
Also, your
multiplyfunction can be improved a lot:a[i][k]is already stored modulo $$$p$$$, there's no need for(a[i][k]%p).a[i][k]andb[k][j], neither $$$i$$$ nor $$$k$$$ should be the third of three for-loops because you jump all over memory this way.Or you can just take implementation from my blog and compare the running time yourself.
Why is at the problem Knight paths the number of moves for k = 2 equal to 15? Shouldn't it be 17? Is the following matrix of paths ending at each tile wrong?
3 0 1 0 1 0 0 0
0 0 2 1 0 0 0 0
1 2 0 0 1 0 0 0
0 1 0 2 0 0 0 0
1 0 1 ...
There is only one way to move from (1,1) to (2,3) in at most two moves, not two ways.
Aha, thanks. What's up with the mod value tho lol, now I have to learn how to use unsigned integers in java.
I don't get it. According to the first sample case, staying at the same square is also considered as a move, so can't the 2 paths from (1,1) to (2,3) be (1,1),(1,1),(2,3) and (1,1),(2,3),(2,3) ? Or are these 2 paths considered the same?
Don't ignore the statement ;p
Staying in one square isn't a move, it's a sequence of 0 moves.
Errichto are the problems still visible after the contest is over?
Yes, you can upsolve after the contest.
Proof that associativity of the matrix "multiplication" still holds if we instead of multiplying values take the minimum? Does associtativity hold for just any such operation that we think of?
Like at problem F it's easy to find a matrix that returns the min paths if multiplied with the min paths of the previous step but I find it really hard to guess why just multipling the auxillary matrixes themselves at first leads to the solution.
If you replace addition by
minand multiplication by addition (I think you meant these replacements), you'll obtain an idempotent semi-ring (see example 1). The associativity of matrix multiplication follows from the properties of this semi-ring.Yeah I meant that. Interesting, thanks. So this is just a special case where associativity holds and thus using other operations wouldn't necessarily keep the associativity?
Yes
As I said somewhere in the video about hard problems (GHI), you shouldn't really try to prove it. Just think if you can combine two matrices into one. If somebody gives you information about best paths of length 4, can you get all the information about paths of length 8? If yes, you're good.
90386255 is giving 0 for all queries . I wrote Same code like yours . What is wrong in this I spend 5 hrs in this question Knight Paths. Errichto
Change
prod.a[i][j]toprod.a[i][k]in matrix multiplication.Next time print some debug information to see what is going on. Or if you want to do it just like some other code, copy-paste some part and see if it works then.
Hey Errichto, is time limit for problem E too strict for java? getting tle on test case 23.
No it's not strict at all. I passed with 265 ms. The trick is to use &((1<<32)-1) rather than %(1<<32). Bit operations are much faster than modulo.
Thank you so much skittles1412.AC with 374ms. I was not expecting my code would be this much fast after using this trick.
This code where I am making a query for the interval [0,n) after every update gives TLE on case 13, whereas this code where I print the value of the node at index 1 of the tree after updating gives WA on case 4. Please help me out, thanks in advance!
Those are long codes, I won't be able to immediately spot a mistake. If your code is too slow, investigate locally which part is a bottleneck. Maybe you need to speed it up twice, maybe the solution is quadratic. And you should analyze the behavior of your program on case 4 yourself, here's a copy-pasted verdict if you don't have access yourself: https://pastebin.com/9KJQBh0D
Errichto In F(Min Path), how to handle the case if there is no path with k edges?
Initialize as infinity.
in your code, if answer > INF/2 then you print IMPOSSIBLE. Could you please explain this in more detail?
You want to check if the path includes any INF. If the path has
kedges, one of them being INF and all others having weight10^9, we'll have total path sumINF - 10^9 * (k - 1). So if the path has at least this path sum, it is "IMPOSSIBLE". INF / 2 is just a lower bound of this value. Hope this helps.Got it... Thanks :)
Errichto Hello, could you tell me why this submission for problem H is timing out? https://codeforces.com/gym/102644/submission/98991255
For sure you have a big constant factor but I'm not sure if that's the reason for TLE. When matrix size is small, vectors work much smaller than arrays. Maybe first run your solution locally (or in CF custom test) and check if you exceed TL by a little bit or if your solution is very slow. If the latter, it likely means your complexity is quadratic so maybe you have a bug in your segment tree.
And use constants instead of copy-pasting value 262144 five times.
Errichto In problem G, by operating (a(i+1)-a(i)) twice i got an equation for a(i) (where i>=(n+2)) has only one constant extra addition of (2*r) and changed coefficients accordingly...here is my submission 105663073 I am getting a wrong answer on test 12.Can you please spot the mistake and rectify my method .Thanks!
Must be an overflow because your output is negative.
Thanks a lot! It got AC :)
seems like there is some problem with the formatting Errichto
Fixed, thanks. Latex didn't like an expression
[[a,b],[c,d]]. Adding spaces fixed it.Do we have to sum (A)+(A)*2+....+(A)*k in problem E ?
Errichto
I need help with problem E. I solved it with the fact that:
So we can use matrix exponentiation for this problem like this:
Each multiplication here $$$M^p*S_0$$$, where $$$0 \le p \le k$$$, represents the number of ways to move with exactly $$$p$$$ steps. So if we need to move with at most $$$k$$$ steps we should consider $$$0 \le p \le k$$$.
We can use the geometric progression formula to get the sum but we need to inverse a matrix so we will deal with doubles which is not a good idea. We can modify the matrix exponentiation somehow to make it accumulate the sum of powers.
I think Errichto is using another approach.
See this