Задача D. "Архитектор Вася"
Эта задача вызвала большие затруднения.В этой задаче достаточно было всего лишь вспомнить физическую статику. Для тех, кто затрудняется припомнить школьную программу, могу порекомендовать Википедию.
Как известно, существует 2 условия равновесия тела (здесь и далее будем считать устойчивое и неустойчивое равновесие неразличимыми, и называть общим словом "равновесие" или "устойчивость", так как в данной задаче нет никакого внешнего воздействия на конструкцию, кроме естесственной силы тяжести и силы взаимодействия кубиков с друг другом), но нам в этой задаче надо будет рассмотреть второй закон равновесия, который мы переформулируем в критерий устойчивости для нашей задачи:
Система кубиков устойчива тогда и только тогда, когда для любой ее точки сумма моментов всех сил, приложенных к этой точке равна нулю. Несложно понять, что это утверждение эквивалентно тому, что система кубиков устойчива тогда и только тогда, когда проекция центра масс этой системы лежит внутри или на границе проекции опоры, на которой расположена эта система кубиков.
Значит, используя этот критерий, будем решать задачу следующим образом: будем в текущую башенку добавлять по одному кубику и проверять, устойчива ли она. Для этого, мы должны проверить, является любой суффикс текущей башенки устойчивым, для этого найдем его центр масс, и проверим критерий. Если он не выполняется, то башенка разрушится, и выведем ее высоту минус один, а если она вся целиком устойчива, то надо вывести число n.
Приведем формулы для координат центра масс некоторых n кубиков:


где:
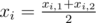 ,
, 
mi = |xi, 1 - xi, 2|3 = |yi, 1 - yi, 2|3










