How to solve this? Tried a lot but didn’t come up an idea.
Problem Link: https://lightoj.com/problem/country-roads
Thanks In Advance
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
How to solve this? Tried a lot but didn’t come up an idea.
Problem Link: https://lightoj.com/problem/country-roads
Thanks In Advance
| Name |
|---|



This is a MST (minimum spanning tree) problem. After knowing the mst the minimum biggest road from a to b is just the biggest road in the mst from a to b
I don't think that's entirely right.
Actually I can prove it.
Let R be the minimum maximum road from a to b. Let's say R is not on the mst. That means that R is bigger or equal to all the nodes that ensure connectivity from a to b. But if a and b are connected by roads that are smaller than R it becomes an absurdity. So R is on the MST by contradiction
Think about this problem in reverse. The shortest path to get from all those cities to city t is the shortest path to get from city t to all the cities, but first, run bfs or dfs from city t and keep a list of the nodes you can visit. Run Dijkstra from node t to all the other cities (Ideal time would be O(E log V) with Fibonacci heap). Then determine if you can visit node i from city t. If you can, output the distance gathered from Djikstra, and if you can't, print Impossible.
The total time complexity of this is T*(E log V) or according to google, 2.86 million, which should pass, depending on the language you're using. If you are having any confusion on how to run a Djikstra, I believe there is an implementation in the CSES book.
Please DM me if you have any concerns about implementation or if my comment did not make sense, and I will try to answer your questions.
Have a nice day!
The thing is, the question is not the minimum distance but the minimum maximum road that you can pass through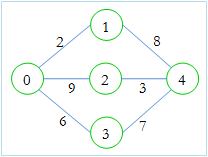 In this image for example the exercise tells that the optimal path is 0-3-4 even though 0-1-4 is the shortest path. There is actually a way to modify the dijikstra to make it work, but it's the same algorithm to find the MST
In this image for example the exercise tells that the optimal path is 0-3-4 even though 0-1-4 is the shortest path. There is actually a way to modify the dijikstra to make it work, but it's the same algorithm to find the MST
You can keep track of all the places that you can reach using DSU from node t. Then if they're not in the same connected components, you can print "Impossible" because there is no way to reach node u from node t. Then you can run Dijkstra's algorithm from node t which finds the shortest path from node t to all other nodes.
Anyone pls help me.