Idea: BledDest
Tutorial
Tutorial is loading...
Solution (adedalic)
fun main() {
repeat(readLine()!!.toInt()) {
readLine()!!.toInt()
println(readLine()!!.split(' ').count { it != "2" })
}
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (awoo)
for t in range(int(input())):
a, b, c = map(int, input().split())
print("1" + "0" * (a - 1), "1" * (b - c + 1) + "0" * (c - 1))
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (Neon)
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, q;
scanf("%d%d", &n, &q);
vector<int> a(n);
for (int& x : a) scanf("%d", &x);
while (q--) {
int x;
scanf("%d", &x);
int p = find(a.begin(), a.end(), x) - a.begin();
printf("%d ", p + 1);
rotate(a.begin(), a.begin() + p, a.begin() + p + 1);
}
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (Neon)
#include <bits/stdc++.h>
using namespace std;
int n, k;
int cur[26];
vector<int> path;
void dfs(int v) {
while (cur[v] < k) {
int u = cur[v]++;
dfs(u);
path.push_back(u);
}
}
int main() {
scanf("%d%d", &n, &k);
dfs(0);
printf("a");
for (int i = 0; i < n - 1; ++i)
printf("%c", path[i % path.size()] + 'a');
}
1511E - Colorings and Dominoes
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 300043;
const int MOD = 998244353;
int add(int x, int y)
{
x += y;
while(x >= MOD)
x -= MOD;
while(x < 0)
x += MOD;
return x;
}
int sub(int x, int y)
{
return add(x, MOD - y);
}
int mul(int x, int y)
{
return (x * 1ll * y) % MOD;
}
int binpow(int x, int y)
{
int z = 1;
while(y > 0)
{
if(y % 2 == 1)
z = mul(z, x);
x = mul(x, x);
y /= 2;
}
return z;
}
int inv(int x)
{
return binpow(x, MOD - 2);
}
int divide(int x, int y)
{
return mul(x, inv(y));
}
string s[N];
int p[N];
int n, m;
char buf[N];
int main()
{
scanf("%d %d", &n, &m);
for(int i = 0; i < n; i++)
{
scanf("%s", buf);
s[i] = buf;
}
p[0] = divide(1, 2);
for(int i = 1; i < N; i++)
if(i % 2 == 1)
p[i] = sub(p[i - 1], divide(1, binpow(2, i)));
else
p[i] = add(p[i - 1], divide(1, binpow(2, i)));
int ans = 0;
int w = 0;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
if(s[i][j] != '*')
w = add(w, 1);
for(int i = 0; i < n; i++)
{
int c = 0;
for(int j = 0; j < m; j++)
{
if(s[i][j] == '*')
c = 0;
else
c++;
if(c > 0)
ans = add(ans, p[c]);
}
}
for(int j = 0; j < m; j++)
{
int c = 0;
for(int i = 0; i < n; i++)
{
if(s[i][j] == '*')
c = 0;
else
c++;
if(c > 0)
ans = add(ans, p[c]);
}
}
ans = mul(ans, binpow(2, w));
cout << ans << endl;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (awoo)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int MOD = 998244353;
const int K = 161;
const int AL = 26;
struct node{
int nxt[AL];
bool term;
node(){
memset(nxt, -1, sizeof(nxt));
term = false;
};
int& operator [](const int x){
return nxt[x];
}
};
vector<node> trie;
int tot;
void add(const string &s){
int cur = 0;
int d = 1;
for (const char &c : s){
++d;
if (trie[cur][c - 'a'] == -1){
trie[cur][c - 'a'] = trie.size();
trie.push_back(node());
tot += d;
}
cur = trie[cur][c - 'a'];
}
trie[cur].term = true;
}
int add(int a, int b){
a += b;
if (a >= MOD)
a -= MOD;
return a;
}
int mul(int a, int b){
return a * 1ll * b % MOD;
}
typedef array<array<int, K>, K> mat;
mat operator *(const mat &a, const mat &b){
mat c;
forn(i, K) forn(j, K) c[i][j] = 0;
forn(i, K) forn(j, K) forn(k, K)
c[i][j] = add(c[i][j], mul(a[i][k], b[k][j]));
return c;
}
mat binpow(mat a, long long b){
mat res;
forn(i, K) forn(j, K) res[i][j] = i == j;
while (b){
if (b & 1)
res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
map<pair<int, int>, int> num;
queue<pair<int, int>> q;
int get(int v, int u){
if (v > u) swap(v, u);
if (!num.count({v, u})){
int k = num.size();
assert(k < K);
num[{v, u}] = k;
q.push({v, u});
}
return num[{v, u}];
}
int main() {
int n;
long long m;
cin >> n >> m;
trie = vector<node>(1, node());
tot = 1;
forn(i, n){
string s;
cin >> s;
add(s);
}
q.push({0, 0});
num[q.front()] = 0;
mat init;
forn(i, K) forn(j, K) init[i][j] = 0;
while (!q.empty()){
int v = q.front().first;
int u = q.front().second;
q.pop();
int x = get(v, u);
forn(c, AL){
int tov = trie[v][c];
int tou = trie[u][c];
if (tov == -1 || tou == -1) continue;
++init[x][get(tov, tou)];
if (trie[tov].term) ++init[x][get(0, tou)];
if (trie[tou].term) ++init[x][get(tov, 0)];
if (trie[tov].term && trie[tou].term) ++init[x][0];
}
}
init = binpow(init, m);
printf("%d\n", init[0][0]);
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include <bits/stdc++.h>
using namespace std;
const int N = 200043;
const int K = 10;
const int Z = 1 << K;
int rem[Z];
int t[N];
int get(int r)
{
int result = 0;
for (; r >= 0; r = (r & (r + 1)) - 1)
result ^= t[r];
return result;
}
void change(int i, int delta)
{
for (; i < N; i = (i | (i + 1)))
t[i] ^= delta;
}
int get(int l, int r)
{
return get(r) - get(l - 1);
}
int ans[N];
int c[N];
int cnt[N];
int n, m;
int ls[N];
int rs[N];
vector<int> qs[N];
vector<int> qs2[N];
int main()
{
scanf("%d %d", &n, &m);
for(int i = 0; i < n; i++)
{
scanf("%d", &c[i]);
cnt[c[i]]++;
}
int q;
scanf("%d", &q);
for(int i = 0; i < q; i++)
{
int l, r;
scanf("%d %d", &l, &r);
ls[i] = l;
rs[i] = r;
qs[l].push_back(i);
qs2[r + 1].push_back(i);
}
for(int i = m; i >= 1; i--)
{
for(int j = 0; j < cnt[i]; j++)
{
rem[i % (1 << K)]++;
int r = i;
while(true)
{
int l = r - Z + 1;
l = max(1, l);
if(l > r)
break;
int diff = i - l;
diff >>= K;
change(l, diff);
change(r + 1, diff);
r -= Z;
}
}
for(auto x : qs[i])
{
int cur = (get(i)) << K;
for(int k = 0; k < Z; k++)
{
int dist = (k - i) % Z;
if(dist < 0)
dist += Z;
if(rem[k] & 1)
cur ^= dist;
}
ans[x] ^= cur;
}
for(auto x : qs2[i])
{
int cur = (get(ls[x])) << K;
for(int k = 0; k < Z; k++)
{
int dist = (k - ls[x]) % Z;
if(dist < 0)
dist += Z;
if(rem[k] & 1)
cur ^= dist;
}
ans[x] ^= cur;
}
}
for(int i = 0; i < q; i++)
if(ans[i] == 0)
printf("B");
else
printf("A");
}










solved 1st 3 ques very fast but got struck on 4th ques,btw nice contest :)
Can someone please explain the solution that's given in tutorial of problem D thanks. I have done a simple solution in that that prints a + ab + ac + .... + az and so on , but I want to understand how the editorial solution works for this
Can you explain your solution? I dont get it
What a solution !
My solution is the same as you and I quickly solve this problem. Amazing.
For 1511B — GCD Length it can be another easy approach
cout<<(ll)pow(10, a-1)<<" "<<(ll)(pow(10, b-1)+pow(10, c-1))<<"\n";
Can u please explain this qn. it took lot of time and i didnt got soln and even not understood the editorial also
First solve the case with $$$c = 1$$$. This is easy, we just need two coprime numbers of a certain length, which we can get in many ways. For example $$$10^{a-1}$$$ and $$$10^{b-1}+1$$$.
Now note that given a solution to the problem $$$a,b,1$$$, we can transform it to a solution of $$$a+c-1, b+c-1, c$$$ by multiplying by $$$10^{c-1}$$$.
thanks , I also got the editorial now
My (faster) solution to G, using binary jumping/lifting/whatever:
It's obvious that for range $$$[L, R]$$$ we want to consider a game of nim where a token at column $$$L\leq i\leq R$$$ corresponds to a pile of size $$$i-L$$$.
Let $$$x[i][j]$$$ denote the xorsum of tokens in the range $$$[i, i+2^j)$$$, where the left border is $$$i$$$ (i.e, a token at $$$i+k$$$ contributes $$$k$$$ to the xorsum).
If we know $$$x[i][j]$$$ for all $$$i, j$$$, the xorsum of $$$[L, R]$$$ can be computed as follows.
(Below, $$$\oplus$$$ denotes xor)
Initialize the xorsum $$$G = 0$$$.
For each $$$k$$$ in descending order, if $$$L+2^k \leq R$$$, do:
1. $$$G = G \oplus x[i][k]$$$
2. If there are an odd number of tokens in the range $$$[L+2^k, R]$$$, further do $$$G = G\oplus 2^k$$$
3. $$$L = L+2^k$$$
At the end of this process, $$$G$$$ is exactly the xorsum we want, so we simply check whether it is $$$0$$$ or not.
So, we want to be able to compute all the $$$x[i][j]$$$ fast — this can be done with a similar process:
1. $$$x[i][0] = 0$$$ for all $$$1\leq i\leq m$$$.
2. $$$x[i][j] = x[i][j-1] \oplus x[i+2^{j-1}][j-1]$$$
3. If there are an odd number of tokens in $$$[i+2^{j-1}, i+2^j)$$$, further do $$$x[i][j] = x[i][j] \oplus 2^{j-1}$$$
Note that we need to be able to check whether some range contains an odd number of tokens, but that's easily done with prefix sums.
Time complexity is $$$\mathcal{O}(mlogm)$$$ for the binary jumping precalculation, and then each query is answered in $$$\mathcal{O}(logm)$$$.
My submission: 112843116
Hi! I didn't really get why you need $$$x[i][j]$$$. It's just a xorsum on a segment. Can't you just use prefix xors too to find it?
My solution is also $$$\mathcal{O}(m \log m)$$$ but uses a different idea and actually needs $$$\mathcal{O}(m \log m)$$$ memory. But it seems like yours needs only prefix sums and xorsums.
It's not quite the xorsum of a segment, more like the shifted xorsum of a segment.
For example, if there are tokens are at columns $$$1, 3, 6, 14, 104$$$, I would have $$$x[2][5] = (3-2)\oplus (6-2)\oplus (14-2) = 9$$$.
I'm not quite sure how you would do the shifting with prefix xors.
Oh, I'm sorry. I misunderstood your explanation.
Nice solution!
Very nice solution!
Fantastic stuff, I did something similar using a segtree with offline queries.
My memory complexity is linear, but total time complexity is $$$O(m \log^2 m)$$$.
The idea is that you can maintain a xor-lazy segment tree, if you want to add/subtract $$$2^k$$$ from all stored elements, you can do that by issuing lazy xor-updates in groups of $$$2^k$$$. You can "visit" all subtractions from $$$1$$$ to $$$m$$$ recursively, starting from low values of $$$k$$$. For example, with $$$m=7$$$, you can have these additions/subtractions in order: $$$[-1, -2, -4, +4, +2, -4, +4, +1, -2, -4, +4, +2, -4, +4]$$$ and you will visit all numbers from $$$1$$$ to $$$7$$$. Notice that $$$2^k$$$ is added/subtracted exactly $$$2^{k+1}$$$ times, so there are $$$O(m \log m)$$$ segment tree updates.
This idea was completely new to me when I first solved this problem.
BledDestForces
I believe that everyone wonders how top 1 risujiroh use O(n^2) brute force to solve G without being hacked. Can someone explain why this solution 112827572 run so fast:)
That is basically because of two things:
1. Using GNU C++17 (64) instead of the 32 bit version.
2. The presence of these two lines at the top:
Remove any of those and you get a TLE :)
Edit: Why so many downvotes? I don't think I said anything wrong. If you don't believe me then try for yourselves.
In this case it seems that you can make it even faster if you submit in C++14 but add the line:
See here (it runs in around 4000ms instead of the 4700ms for the original). I'm not sure how exactly this whole thing with pragmas works, this was just an experimental discovery.
Another thing that seems to contribute to it passing is the usage of
Instead of something like
See here. Again, not at all sure why this makes such a difference, but it does.
Maybe someone can say why these things are the way they are?
Could someone pls tell the combinatorics / dp approach for E ? I saw in the announcements page but is very unclear.
we can do it in the following way,first of all lets calculate what will be the answer if we would have 1 segment with length i that contains only 'o'.its can be done in the following way
cnt_odd[i] = 2^(i-2) * cnt_odd[i - 2];dp[i] = dp[i - 1] *2 + cnt_odd[i -1]where cnt_odd[i] it is mean how much segments [0..i] that has sufix wich contains only '0' and has odd len. than for each consecutive segments of 'o' ans+=dp[len of that segment ] * (count of all possible сoloring of all other matrix).we should do it for horizontal and vertical segments. it's may become more clear if u look at code 112952569. Also i can explain better how we calculate cnt_odd or othere things if needed.
P.S sorry for my pure english)
Yeah. Could you pls explain that (calculating count odd ad etc) ? Also how do you merge after calculating dp arrays horizontally and vertically ?
first of all lets name strings that has sufix which contain only symbol 'o' of odd len good.
cnt_odd[1] = 1. becouse string "o" is good. As well as “**”
cnt_odd[2] = 1. becouse there is string "*o"."oo" has even len so its not good.
let assume that we have string of len i that has last symbol equal to 'o'. Than to be good (i-1)-th symbol of that string should either be '*' than we dont care about others symbol so there can be all possible coloring 2^(i-1).Otherwise (i-1)-th symbol is 'o',so to be good string [0..i -2] should be good as well.so cnt_odd[i] = 2^(i-1) + cnt_odd[i -2].
Now about merging.We have some horizontal consecutive segments of 'o' and some vertical.Let solve them separately.we know that 1 consecutive segment of len i create dp[i] domino. however it will create dp[i] domino for every of possible coloring of the rest of matrix.For example we have segment "ooo" and "o" than answer will be 6 becouse segment "ooo" create 3 domino if second string colored red and 3 if second string colored blue.So 1 segment add to the answer len * 2^(count_of_white -len).
I dont know how to explain why we can do separately for horizontal and vertically but i think that is not hard to undestand if u think a little.
has it become clearer,or should i try to explain one more time? Do u also need an explanation how we calculate dp?
Can you explain how you got the transition function for the dp i.e the relation
dp[i] = dp[i - 1] *cnt_odd[i -1]i have mistakenly write not correct formula in the post(in a code its correct). I am realy sorry for that.
So correct formula is
dp[i] = dp[i -1] * 2 + cnt_odd[i-1].if we know an answer for segment of len (i — 1).Than let us take a look at a segment of len i.We can see that answer for dp[i] is at least 2-times bigger becouse we will add at least dp[i -1] if we would color i-th element in blue and add at least dp[i -1] if we would color i-th element in a red.However for each segment [0..i-1] that has sufix of only 'o' and its len is odd we will add one more domino. Has it become more clear or should i explain anything more? P.S take a look at code it's may become more clear 112952569Sorry , I could not understand the explanation . Can you explain this a bit more ( with a simple diagram , if possible ).
For problem E, can anyone tell the way to find the OEIS sequence (incase anyone else did by finding contributtion method).
In problem D how will we get a Euler cycle of length k*k + 1, do we also have to add self loop for that, because without that you cannot get an Euler cycle of k*k + 1, can someone explain, possible taking example of k = 3.
This Explanation might help you. Video Explanation
How to find eulerian cycle in 1511D - Min Cost String
can someone explain e more properly?using dp etc
I problem F I had slightly different approach. I tried to compute $$$DP[L][i][j][k]$$$ which would mean the number of pairs of chainwords, such that first of them has length $$$(L + i)$$$, second $$$(L + j)$$$ and last part of longer chainword comes from $$$k$$$-th word. We can compute it quite straightforward without using any kind of tree structures. All we have to check is whether some parts of words match. We just see that it is enough to store only $$$((d * (d - 1)) / 2) * n + d$$$ interesting states (though we don't have to use symmetry to pass tests).
Code: https://pastebin.com/04kf681r
Was anyone else confused by the legend of F, thinking it meant count the number chainwords that have resolved ambiguity? This isn't the case tho, right?
Is this rare way to solve B...?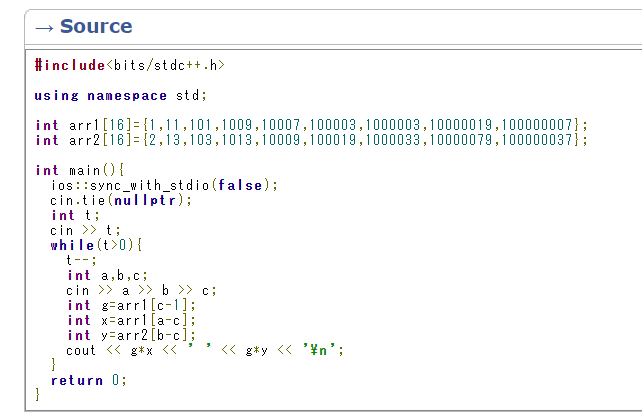
Lol I did the same thing, searching for prime numbers that big was a real hassle though :P
I also had a fun solution while preparing the task.
I did this too, but on my alt account.
" Now, let's suppose there are two strings i and j such that cnti−cntj≥2. Then, if we somehow reduce the number of occurrences of the string i by 1 and increase the number of occurrences of the string j by 1, the cost will decrease " What does that mean ?
"strings" here means pair of two characters like aa, ab, ac, etc.
Actually the solution of many participants is easier & simpler than the editorial
Can someone help me to in problem d (min cost string)? What's the intuition behind the greedy approach. like this
Taken from submission (random)
Can someone explain how to produce your logic for questions similar to problem B during competitions? I solved C and D in the second hour but I couldn't solve B after wasting the first hour in virtual participation...
Let t = gcd(x, y)
=> x = At
y = At
So I choose t = 10^(c — 1), then choose A = 10^(a — 1 — (c — 1)), B = 10^(b — 1 — (c — 1)) + 1
It can be proven that gcd(A, B) = 1, so gcd(x, y) = t
For problem F, I generate the input that requires 141 states.
And I believe this to be an upper bound. If there is no string that become other string prefix, the number of states will be at most 49. If there is a string that become other string prefix, the number of states will be at most 161 — 20 = 141
In the way I modeled the problem this case takes only 99 states, so I must be doing something different.
I imagined the graph as a finite state machine where each accepting path is a way to construct a possible chainword. The states are pairs $$$(u, v)$$$ where $$$u$$$ and $$$v$$$ are proper (and possibly empty) suffixes of a word in the dictionary, and $$$u$$$ is a prefix of $$$v$$$, and they represent a look-ahead of the chainword we are building. The initial and only accepting state is $$$(\varepsilon, \varepsilon)$$$.
Edges from $$$(u, v)$$$ to $$$(u', v')$$$ represent a way to add one character to the chainword, they fall in three cases:
$$$u$$$ and $$$v$$$ are non-empty so $$$u'$$$ and $$$v'$$$ are equal to $$$u$$$ and $$$v$$$ resp. minus the first character in each.
$$$u = \varepsilon$$$, so $$$u'$$$ is a word in the dictionary (again, minus its first character) to continue the chainword from $$$\varepsilon$$$.
$$$u = v = \varepsilon$$$, so $$$u'$$$ and $$$v'$$$ represent two words in the dictionary that are prefixes from one another to start building a chainword.
I believe this approach is very similar to using a trie but there must be a difference somewhere I am not seeing. Is it that I am merging some states into one?
Code
The writer's solution contains unnecessary states. For example, ("abcde", ""), ("abcde", "abc"), etc. The number of unnecessary states is 42, and your answer removes these states.
Can someone please explain me how the logic of D work?
It works on the concept Euler circuit. you make every letter up to k as a vertex in a graph and connect every vertex to every other one because we can pair every letter with every other one.
after that you print the euler cycle of graph which will general all distinct string of size 2 using k letters. and after that you can just repeat this string.
Euler circuit says that you can visit every edge of the graph only once. and every edge contains two letter so you will be visiting every substring of size 2 as the graph is complete graph.
This is the concept of the problem.
now you can implement it by Euler circuit and graph and all. But as I didn't know how to do that I did it using two loops.
Thank you
Your Welcome :D
Please explain your 2 loop solution?
first loop I'm starting with a to less than k and adding that aplhabet to string and in the jth loop I'm starting from i + 1, that is from the next letter which I took in i loop.
for example: if in the ith loop I have added b to the string then the jth loop I will start from c and not from a because ba would already have occured in the previous iteration when i was a.
for a, b and c
first iteration i = 0 string a then in jth loop i'm starting from b and adding ab, ac .. so string will be a + ab + ac => aabac
the i will become 1 I will add b string => aabacb
now j will start from c , because you can see ba has already occured in previous iteration
so string will be aabacb + bc and so on
This Video Explanation might help you.
Problem G can be solved with MO.
Can you explain how to shift the bounds (of MO, i.e. l, r) fast enough?
1511G - Chips on a Board Isn't complexity of solution from editorial should have log N outside of square root?
I want to share my solution of 1511G - Chips on a Board.
All we need to do is to find XOR of $$$c_i - L$$$. For details "why?" look into editorial. I'll describe here how I calculate it. Notice that we can represent each number as two digit number XY in some base $$$2^k$$$. Then $$$c_i$$$ is some xy and L is XY. But this is the same as XOR all (y-Y) and (x-X) but some of them will turn into (x-X-1) when y < Y because of carry. My idea was to view it as points in table, where X digit is on X axis, and Y digit is on Y axis. Notice, that size of table is $$$2^{2k}$$$, so with appropriate k it is O(m) memory. Then we need to XOR all xy-XY. Then, to count how many times there is x among $$$c_i$$$ is just segment in column which can be calculated as prefix sums. And, to count how many times there is y among $$$c_i$$$ is just segment in row which can be calculated as prefix sums. But here is the problem: how can we tell should we subtract 1 for carry or shouldn't? This is most tricky part of whole solution. It turns out that we subtract 1 when y < Y, but it also can be calculated as prefix sum! Because we need to find out how many of x from column we should subtract 1 and how many we shouldn't but within single column x there are exactly numbers xy where v < Y we should subtract 1, and v >= Y we shouldn't, because carry won't happen. So, we can make two tables of prefix sums: for columns and rows. Each table has $$$2^k$$$ in both dimensions, and then for each X, and each Y we calculate prefix sum which is $$$O(2 \cdot 2^k)$$$ for each request. Overall complexity then is $$$O(n+m+q\cdot\sqrt{m})$$$ 113146022
can you explain gcd length question i didnt get it
This Link might help you. Video Explanation
Can someone suggest some more problems which can be solved using probability for counting as mentioned in the editorial. I understood the solution but I want to practice more such problems. Thanks in advance :)
Alternative solution for problem 1511G - Chips on a Board
Consider each bit $$$b$$$ separately and keep a data structure that contains the remainder of the position of the coins in a suffix, modulo $$$2^{b+1}$$$. It should handle these operations:
So you can use a Fenwick tree with Venice trick for each bit.
Total complexity: $$$O(n \log^2(n))$$$.
113692737
Nice solution! Thanks for sharing.
Is there any similar problem on codeforces as problem F but maybe of lower difficulty. I cannot understand the editorial at all.
Can some one explain the complexity in 3rd question
For the first time we find a min colour card, we will have to traverse the entire deck to find it, but in all successive calls we will only have to traverse at max k elements because only one same card per colour is being put to the beginning of the deck. Hence, complexity O(nk + qk)
Can someone explain editorial's solution for problem D min cost string ?
Or can anyone explain the approach by eulerian path?
I'll try to explain the editorial's solution. The cur array is tracking how many unique vertices/characters have visited the current vertex/character. The dfs is essentially creating a path where it visits every edge between every vertex once. So every vertex will be visited by k vertices, including itself. And in main, if the path is too small, then it is simply repeated until there are n characters. But I think this construction is a lot harder to understand. The main idea is that we want to minimize the number of substrings of size 2 that are the same. That means we want to "use" every possible length 2 substring in our path before we repeat any. This can be represented by a Eularian cycle in a graph, where each character is a vertex, and every vertex is connected to every other vertex. A eularian cycle will always visit every edge once and start and end on the same vertex. So how do we find this path? In this case, we don't have to actually create a graph, we can just simulate it. This guy's submission is really elegant. https://codeforces.com/contest/1511/submission/112810190 The reason why you add 'a' + i to the string before the inner for loop, is that we also want to include the strings of length 2 that are just the same character, like "aa", and "bb". However, the way the for loops are set up, we will miss these strings. So we add, the 'a' + i before the inner for loop, so the first 3 characters of that iteration become "aab" for example. We don't want "aaab", because that will lead to repitition of "aa" twice, and that violates the Eularian path. Then we just repeat this constructed cycle until we have length n.
Amazing explanation, thanks!
I had skipped this question after a spending a day since I could not understand the editorial or its solution.
can someone please help me in question D.
i want to solve it without DFS and BFS as i dont know it yet.
can we solve it constructively??