357A - Group of Students
In this problem you need to iterate over all possible values of passing rate from 1 to 100 and for each value calculate the sizes of two groups.
357B - Flag Day
Let's process the dances in the given order and determine the colors of dancers' clothes. If there are no dancer from some previous dance, we can give the dances different colors arbitrarily. And if there is such dancer, we already know the color of his clothes. So, we arbitrarily distribute the other two colors between the remaning two dancers.
356A - Knight Tournament
Let's the current fight (l, r, x) consists of K knights fighting. Then all we have to do is to find all these knights in time O(K) or O(KlogN). There are several ways to do that, let's consider some of them.
The first way is to store the numbers of all alive knights in std::set (C++) or TreeSet (Java). Then in C++ we can use lower_bound method to find the first knight in the fight that is alive, and to iterate over this set, each time moving to the next alive knight. In Java we should use subSet method.
set<int> alive;
for (int i = 0; i < n; i++)
alive.insert(i);
for (int i = 0; i < m; i++) {
int l, r, x;
scanf("%d%d%d", &l, &r, &x);
l--, r--, x--;
set<int>::iterator it = alive.lower_bound(l);
vector<int> toErase;
while(it != alive.end()){
int cur = *it;
if(cur > r)
break;
if(cur != x){
toErase.pb(cur); answer[cur] = x;
}
it++;
}
for (size_t j = 0; j < toErase.size(); j++)
alive.erase(toErase[j]);
}
The second way is to define array next with the following meaning:
- if knight v is alive, then next[v] = v;
- if knight v is out of tournament, next[v] points to some knight u (next[v] = u), such that there are no alive knights between v and u;
To find the first alive knight starting from the knight v we need to follow this links until we find the first knight w with next[w] = w. In order not to pass the same links too many times, we will use the trick known as path compression (it is used in Disjoint Set Union). Note that you should handle the case when the current knight is the last knight and is out of tournament.
int getNext(int v){
if(next[v] == v)
return v;
return next[v] = getNext(next[v]);
}
...
int cur = getNext(l);
while(cur <= r){
if(cur == x){
cur = cur + 1;
}else{
answer[cur] = x;
next[cur] = cur + 1;
}
cur = getNext(cur);
}
356B - Xenia and Hamming
Let's denote the length of the first string as lenX, the length of the second string as lenY. Let L = LCM(lenX, lenY). It's obvious that L is a period of the long strings a and b, so we can find the distance of its' prefixes of length L and multiply the answer by 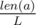 . Let's fix the position i in the string x and think about all characters from the second string it will be compared with. It it easy to conclude that it will be compared with such yj that i ≡ j (mod g), where g = GCD(lenX, lenY). For each possible remainder of division by g and for each character c we can calculate count(r, c) — the number of characters c that appear in y in such positions j that j mod g = r. When calculating the Hamming distance, the character xi will be compared with exactly count(i mod g, xi) characters from y that are equal to it, all other comparisons will add one to the distance.
. Let's fix the position i in the string x and think about all characters from the second string it will be compared with. It it easy to conclude that it will be compared with such yj that i ≡ j (mod g), where g = GCD(lenX, lenY). For each possible remainder of division by g and for each character c we can calculate count(r, c) — the number of characters c that appear in y in such positions j that j mod g = r. When calculating the Hamming distance, the character xi will be compared with exactly count(i mod g, xi) characters from y that are equal to it, all other comparisons will add one to the distance.
private void solve() {
Scanner in = new Scanner(System.in);
long n = in.nextLong(), m = in.nextLong();
String x = in.next(), y = in.next();
int lenX = x.length(), lenY = y.length();
int g = gcd(lenX, lenY);
long L = lenX * (long)lenY / g;
long answer = L;
int[][] count = new int[g][26];
for (int j = 0; j < lenY; j++) {
count[j % g][y.charAt(j) - 'a']++;
}
for (int i = 0; i < lenX; i++) {
answer -= count[i % g][x.charAt(i) - 'a'];
}
System.out.println(answer * (n * lenX / L));
}
356C - Compartments
In the problem you should come up with some right greedy algorithm. One of correct approaches acts as follows:
- Firstly, it joins all "twos" and "ones" (to get "threes"). Several "ones" should be moved.
- Then you should consider two cases depend on amounts of "ones" and "twos". If initially you have more "ones", you should try to join remaining after the first point "ones" into groups of three. If initially you have more "twos", you should try to join remaining after the first point "twos" into groups of three. You can get two "threes" from three "twos".
- After the first point and the second point some "ones" or "twos" can remain. You shouldn't come up with common solution. Else you should just to consider all possible cases.
To solve the problem you should follow your common sense (is it greedy?). Writing naive solution (bfs search) for stress purposes is not so bad for proving correctness of your solution.
356D - Bags and Coins
It's easy to see that bags and their relations "lies directly in" should form directed forest. Each vertex should be given value ci — the number of coins in the corresponding bag. Let's denote the sum of values cj in the subtree of vertex i as fi. The following conditions should be met:
- fi = ai
- then sum of fi of roots equals s.
It's clear that one of the bags with largest ai must be the root of some tree. It's quite easy to see that the solution exists if and only if there exists a subset ai1, ai2, ..., aik such that ai1 + ai2 + ... + aik = s and this subset contains at least one bag with the largest ai. It's obvious that it is necessary condition, the sufficiency is also easy to see: let's suppose we have such subset. Then all bags from the subset, except one of the largest, will be roots of the signle-vertex trees (i.e. ci = ai for them). All bags that are not in the subset we will consequentially put into the largest bag, forming the "russian doll" (this tree will be directed chain).
So, we reduced the task to the well-known subset-sum problem: from the items a1, a2, ... an find the subset with the given sum s. This problem is NP-Complete, and with these constraints is solved in a following way: let T(i, j) = 1 if it is possible to obtain sum j using some of the first i items, and T(i, j) = 0 otherwise. Then 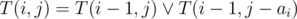 . The i-th row of this table depends only on the previous row, so we don't have to store the whole table in memory. Also we should use the fact that the values of the table are zeroes and ones, and we can use bit compression and store each row in an array of int's of size
. The i-th row of this table depends only on the previous row, so we don't have to store the whole table in memory. Also we should use the fact that the values of the table are zeroes and ones, and we can use bit compression and store each row in an array of int's of size 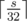 . To get the i-th row, we should calculate the bitwise OR of the previous row and the previous row shifted to the left by ai positions. That is, we can find out whether it possible to obtain the sum s in approximately
. To get the i-th row, we should calculate the bitwise OR of the previous row and the previous row shifted to the left by ai positions. That is, we can find out whether it possible to obtain the sum s in approximately 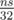 operations. To find the actual way to obtain s, we need to use the following trick: for every possible sum j we will remember the value first(j) — the number of such item that after considering this item it became possible to obtain j. This allows us to restore the solution.
operations. To find the actual way to obtain s, we need to use the following trick: for every possible sum j we will remember the value first(j) — the number of such item that after considering this item it became possible to obtain j. This allows us to restore the solution.
356E - Xenia and String Problem
During the contest most of participants write the solutions that are very similar to the author's one. One of the author's solution uses hashes (but there exist solution without it), you can see short description of the solution below:
For each position i calculate with hashes the maximal value of Li, such that substring s[(i - Li + 1)..(i + Li - 1)] is Gray string. Also, calculate the maximal value Pi, that substring s[(i - Pi + 1)..(i + Pi - 1)] differs from some Gray string in at most one position. You can see that Pi ≥ Li. If Pi > Li, also remember position and letter in the position, that differs Gray string and the substring.
You can see, that if we don't need to change letters, then the answer for the problem is
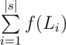 , where f(L) = 12 + 32 + 72 + ... + L2. So, calculate an answer without changes.
, where f(L) = 12 + 32 + 72 + ... + L2. So, calculate an answer without changes.Next, iterate through all positions and letters in it. What is the new answer for the problem? Look at all Gray strings that occurs in our string and touches our fixed position. After we change this position the string will not be Gray string anymore (so we should subtract the squired length of the string from our answer). Look at all Gray strings that differs in exactly fixed position from some substring of the string. If we change the letter in the position to the fixed letter, all such strings will be added to the answer (and we should add their squired lengths).
Summary, with Pi and Li we need to calculate for each position and letter, how the answer differs if we change the letter in the position to the fixed one. For that reason we should use offline update (+=) on the segment. After the values will be calculated we can update our answer with all possible values.











Hi, would you please help me to clarify the problem 356B — Xenia and Hamming " It it easy to conclude that it will be compared with such yj that i ≡ j (mod g), where g = GCD(lenX, lenY)."
How to get that conclude?
Thanks
let's say ith character in the kth repetition of x is matched with jth character in the pth repetition of y
(k * x + i) mod gcd = i mod gcd (p * y + j) mod gcd = j mod gcd
I still can't get it. How do we conclude the gcd part? Would someone explain it in more details, please?
Let us consider the ith character in the xth repetition of the first string. And let us assume that it is matched with the jth character of the yth repetition of the second string. Then - (x*Len1+i) = (y*Len2+j) Should be true. Where Len1 and Len2 are the lengths of the first and second strings respectively.
If g = gcd(Len1,Len2), then we can write the equation as - (x*Len1+i) %g = (y*Len2+j) %g Hence, we get- i%g = j%g
For DivI A, I think it is more convenient to use the
erasemethod inset:I had a different solution for Div 1 C, which I think is easier to prove to yourself and harder to miss a case in.
Let's sort the numbers. Then, intuitively, it seems that there should exist a border in sorted train which splits the carriages into two parts — carriages with no students in it [first part], and carriages with 3 or 4 students in it [second part] (I would be very glad if someone could give me general proof for that [if more people were allowed in carriages and not just four] — maybe this isn't true in general case).
So let's check all possible border locations. Now that we have it fixed, let's denote four values, which can be computed in O(1) using partial sums:
Now, source <= free should hold, otherwise this scenario is impossible.
If source >= target (aka, transferring all students from first part to second will do), then we mark source as a potential answer.
Otherwise, we have to use students from second carriage, so if additional >= (target-source), then we mark target as a potential answer.
These are all the cases we have to worry about and the total complexity is O(N log N) or O(N) if you're bothered with doing count sort.
The proof for the first statement. It is clear that we don't need to empty any carriage with more than 3 students. Also, emptying a carriage with 2 students and filling a carriage with 1 student is not optimal, since it is better to put that 1 student in the carraige with 2 guys. Thus there is such a border, and it is somewhere before the first carriage with more than 2 guys.
UPD: sorry, I misunderstood, it's only a proof for a maximum of 4 people in carriage.
Okay, the proof for the general statement is essentially the same. Suppose we empty a carriage with b people and fill a carriage with a people, a < b. It is clear that we better empty the carriage with a people, hence contradiction.
Would someone point out why I'm getting a wrong answer on test 26 for this submission 4808669 and 4799577 on 356B - Xenia and Hamming
Are you sure you are using 64-bit integers? (like long long)
yes, I used
unsigned long longIn Problem "356D — Bags and Coins" , can we write masks in unsigned long long , so we can solve the problem in n*s/64 operations ?
But you should keep in mind that oprations on long long are slower than operations on int
Yes , I know time will be the same , but those bitmasks was needed on opencup contest , where 64 bits didn't passed (WA) , 32 passed , so I am asking what is wrong with 64 bit integers .
There is a typo for problem E: f(L) = 12 + 33 ...
Am I the only one who thinks that Compartments was an ugly problem? I got the wrong the wrong idea and I had to deal with eleven or thirteen cases and of course I had holes in my solution, but even when got the good idea this wasn't a nice problem. And editorial for this task is the best proof.
I'm not fond of it, but it's not really that bad. There is a solution in which you don't have any cases or choices to make. If you try to fix the number of compartments in the final solution, the number of 3-compartments and 4-compartments is uniquely determined. Looking at the input and the fixed candidate solution in sorted order you may have something like:
Say you fix the number of compartments to 5.
1 2 2 3 4 4
0 3 3 3 3 4
You just add the absolute difference for each position and then divide by 2. You can do that efficiently by using frequencies instead of values in about 3 — 4 lines of code.
It's the kind of problem that teaches you to keep things simple (don't assume anything, jut try everything) which is a welcome reminder from time to time.
Yes, I know that solution (marcin_smu told me that) and I think that this is the nicest one. Indeed, I fell in trap of thinking "this can be done in any way!" and choose the wrong one, but as you can see, even author of this problem wasn't aware of that solution without any case-analysis.
Wrong tutorial? 357 B -FLAG DAY What if this is the test case n=6 m=3 dance1 1 2 3 dance2 1 4 5 dance3 4 2 6
the algorithm could fail on it.
Please, read the statement carefully before asking such questions. This case is not valid because in dance 3 we have two dancers (2 and 4), who had participated in some of the previous dances.
I am sorry, didnt get the problem statement. Now its clear. Thanks
In the second solution for Knight Tournament, if we set "next[cur] = cur + 1;", my understanding is we would always end up traversing each element, though we would process only the ones which are alive. Instead I think we should do
next[cur] = getNext(cur + 1); cur = next[cur];
Is my understanding correct or am I missing something here ?
magic happens in getNext function :)
I'm trying to solve prob.A with dsu, also used path compression. Even though all test cases must use same amount of mem for my code, got MLE for 22nd case although n=100 http://ideone.com/MUWaHY
My solution for div1 A gives TLE, but approach is same as given in editorial. Any idea why? Iam simply deleting elemnts in each match, so the worst case complexity is O(n*log^2(n)), when each match has only 2 knights because code
It's long time! Do you understand now, what was the problem ? I face same problem Here is my code : CODE
How to solve Div1A (Knight Tournament) using Lazy Propagation on Segment Tree. I am unable to build up the concept how to make Segment Tree and how to handle it for queries. Can anybody help me please?
hello , i just finished that problem ,
create a segment tree where you keep in each node the number of killed knight in that interval
and each time you get a query ,divide that interval into 2 intervals ( to ignore the alive knight )
and execute an update on the tree , PS( i didn't use lazy propagation technique )
you can see my code here and ask me any question , submission
I had finished the problem too, actually I was learning the lazy Propagation concept in segment tree. So, I was trying to solve this problem by Lazy Propagation. However, problem can be solved without using Lazy Propagation too.
i think that sometimes your update function works in O(N)
In the seg tree he is not doing point update instead doing range update but as the range of update is decreasing so it works.
Hi, So my method is the same as the one in the editorial,I used std::set but I cant figure out why my solution is getting TLE,please help.. 28733152
Faced the same problem. Have a look to this: http://codeforces.com/blog/entry/19043
Knight Tournament also solvable with ST (each node is true if there's any alive leaf, false otherwise)
Can you explain how to solved Knight Problem Use Segment tree please?,it will really helpful. Thanks in advance
Each knight is a leaf in the segment tree. Also, every leaf has the state 'true' if he's alive ('false' otherwise). A node in the segment tree has state 'true' if there's at least one knight alive in that sub-tree. So, every query kills all the knights in the given range, assigns the id of the killer knight accordingly, and also updates the states of every node. This state-updating thing is to avoid traversing dead ranges with no alive knight. Hopefully, it's clearer now how to use ST here :)
That means here we need two arrays, one to store the states and the other to store the IDs ,right?
Exactly
Thank you so much. This was very helpful.
there is some problem with the judge MikeMirzayanov Nerevar https://codeforces.com/contest/356/submission/80592110 https://codeforces.com/contest/356/submission/80592719 both of these are same but only 1 got AC