probelm : http://www.lightoj.com/volume_showproblem.php?problem=1318 code :http://pastebin.com/HVyHX3hx verdict: wa
I have doubt that my approach to this problem is correct. I am gonna describe my idea in brief , please somebody verify where am I wrong.
The basic task is to count number of valid pairs that satisfies constraints mentioned in the problem. If we have 'K' alphabets,how many pair of strings of length 'L' we can get where the strings of a pair has a mismatch at exactly 'M' positions.
I tried to convert the problem into coloring a 2*L grid. We have to color a 2*L grid with K colors where exactly L-M columns has to be colored with same color and the rest columns must have two different colors in their cells.
we can choose (L-M) fixed columns in C(L,L-M) ways and we can color each column with any of the K colors. Therefore we have K^(L-M) ways for L-M columns.
(Now we have rest M columns where we need to ensure mismatch. For each column we can put any of the K colors in the first row and for the next row we have K-1 choice. Therefore we have K*(K-1) ways to color a column. There are M such columns. Therefore we have (K*(K-1))^M) ways to color these columns. )*#confusion_1
Therefore we have N= C(L,L-M) * K^(L-M) * (K*(K-1))^M) pairs.
(The pairs always repeat each other).*#confusion_2 So, I toke N=N/2 , not directly , mathematically
I am not sure about #confusion_1 and #confusion_2 (enclosed by a first bracket). Someone please verify the bug of my idea.











The result is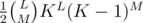 for M > 0 and KL for M = 0.
for M > 0 and KL for M = 0.
We have KL words, and for every one of them (as the 1st word of the pair), we have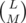 ways to choose the mismatching positions in the 2nd word; we can put any of the remaining K - 1 letters in every mismatching position and just 1 (the same) letter to put in every matching one. If M > 0, the 2 words are different, so each pair is counted twice here and we need to divide by 2; for M = 0, it's counted just once.
ways to choose the mismatching positions in the 2nd word; we can put any of the remaining K - 1 letters in every mismatching position and just 1 (the same) letter to put in every matching one. If M > 0, the 2 words are different, so each pair is counted twice here and we need to divide by 2; for M = 0, it's counted just once.
My guess is that you don't consider the special M = 0 case, or don't do the modular division by 2 properly. (I'm too lazy to read the code.)
Yes, for M=0 we don't have to divide by two. A came up with this case latter by matching the result of my brute force code.Am I right? But why this happening so, I have no idea. Many many thanks for reviewing my idea. It helped me a lot.
thanks Xellos , finally got AC! nCr gave me the pain that took a long for me to get acc.