Hi all!
I invite you to participate in the gym contest LU ICPC Selection Contest 2023 on Nov/08/2023 17:35 (Moscow time)! The onsite contest has been held on October 13th in Riga to select two teams from the University of Latvia to CERC 2023. Here's the headline of the local poster (in Latvian):

The contest has been prepared by me, cfk and Pakalns. Hopefully you'll find the problems interesting!
























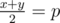 .
.
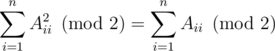
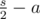 other pairs. Among them, for
other pairs. Among them, for 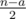 pairs both members belong to
pairs both members belong to 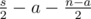 pairs none of the members belong to
pairs none of the members belong to 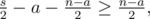
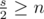 , as given in the statement.
, as given in the statement.
 .
. .
.

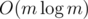 , because of the sorting.
, because of the sorting.
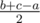 ,
, 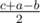 ,
, 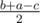 . If the problem asked only the possibility of building such a molecule, we could just check if there exists (possibly degenerate) triangle with sides
. If the problem asked only the possibility of building such a molecule, we could just check if there exists (possibly degenerate) triangle with sides 
 can be obtained with
can be obtained with 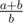 and
and 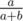 with
with 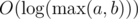 . Problem authors:
. Problem authors: 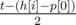 seconds, then
seconds, then 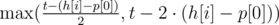 . Then we move the pointer onto the first unread track, and repeat the algorithm for
. Then we move the pointer onto the first unread track, and repeat the algorithm for 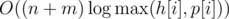 . Problem authors:
. Problem authors: 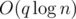 . Problem author:
. Problem author: 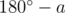 . Their sum is equal to
. Their sum is equal to 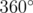 , because the polygon is convex. Then the following equality holds:
, because the polygon is convex. Then the following equality holds: 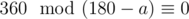 .
.

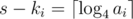
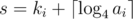
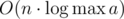 .
.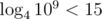 . So it is enough to find the first square that fits from range
. So it is enough to find the first square that fits from range 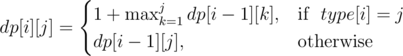
 .
.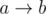 we can immediately update the maximum downwards flow of
we can immediately update the maximum downwards flow of 


 (top-right)
(top-right) 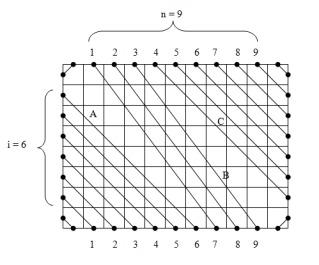
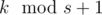 (top-right segments continue as corresponding left-bottom segments). Thus we can describe it as a permutation
(top-right segments continue as corresponding left-bottom segments). Thus we can describe it as a permutation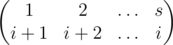
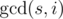 and their length is
and their length is 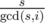 . So all these cycles have the same length. Denote the remaining segment types as some letters (in picture A, B, C). Then not only the length, but the strings describing the cycles are also the same, but can be shifted cyclically (here the direction of the cycles also is important). Besides, we know this string from the correct arrangement cycle. Thus we need to compare all the remaining given arrangement cycle strings to this string, considering cyclic shifts as invariant transformations. For each string this can be done in linear time, for example, using the Knuth-Morris-Pratt algorithm. When we find a cyclical shift for each cycle, we can position its relevant columns and rows according to the end arrangement.
. So all these cycles have the same length. Denote the remaining segment types as some letters (in picture A, B, C). Then not only the length, but the strings describing the cycles are also the same, but can be shifted cyclically (here the direction of the cycles also is important). Besides, we know this string from the correct arrangement cycle. Thus we need to compare all the remaining given arrangement cycle strings to this string, considering cyclic shifts as invariant transformations. For each string this can be done in linear time, for example, using the Knuth-Morris-Pratt algorithm. When we find a cyclical shift for each cycle, we can position its relevant columns and rows according to the end arrangement.
