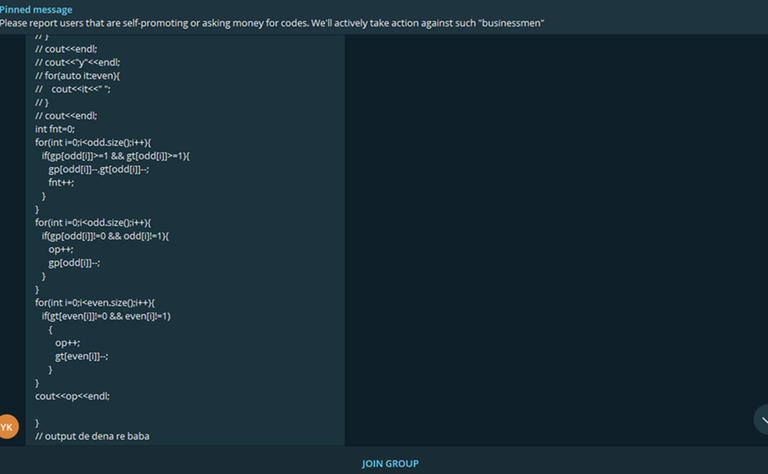
Well, As my friends sent me some screenshots from his messages, I am now sure that he is one of the new big cheaters in codeforces, sailikpandey, I've warned him many times in DM in Cf but he didn't care now I think it's time to share the proofs :
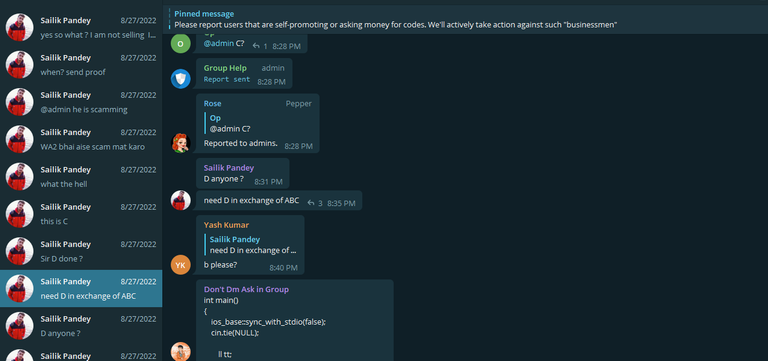
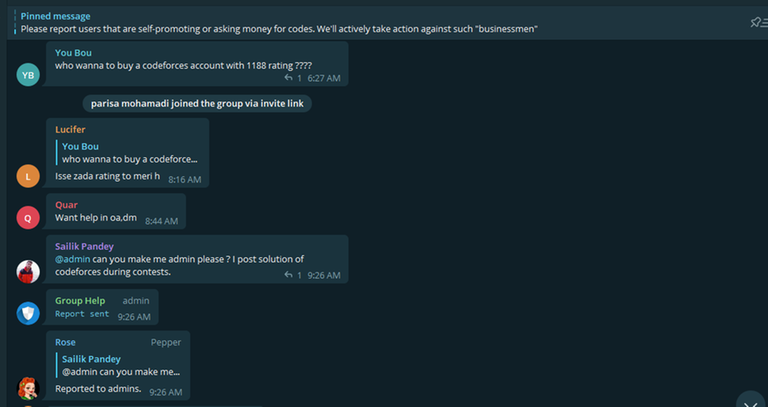
Also immediately after receiving my messages and not accepting that he is a cheater, He changed his username on Telegram as you can see the difference in the last picture and the picture below :
His strategy is writing many comments that makes the code unreadable, And when I asked him why you do this he says it's because to make hackers not able to read my code but as you can see this is the code which has been revealed in the group last night for Edu 135 problem C (Which is a very bad thing) :
And this is his submission : 171412386
If you compare his code with the given in screenshot you see no difference, Also All of his contests submissions contains heavy and many comments which is a violation of codeforces rules, Please Mike or other people if you can do sth to stop such cheaters, Thanks, MikeMirzayanov
P.S : Congrats cheater, You became specialist sailikpandey :)