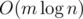We can find all information about i-th car collisions in the i-th row of the matrix A. More specific, if there is at least one 1 or 3 at i-th row, then i-th car isn't good (it was turned over in at least one collision). Otherwise, i-th car is good. We just need to check this condition for each car.
One can see, that if si = ti for some i, then the value of pi isn't important for us. Really, if we make pi equal to si then it also be equal to ti. And if we make pi not equal to si then it also be not equal to ti. So, we have an answer that is closer or further to both of s and t.
So we interested about such position i that si ≠ ti. If we make pi equal to si we make p further from t. If we make pi equal to ti we make p further from s. It means that we need to divide these positions into two equal parts to have equidistant string. For example, we can make first of these positions closer to s, second closer to t and so on. If the number of these positions is even, we find an answer, if it is odd, answer doesn't exist.
Time complexity — O(n).
One can solve this problem using dynamic programming or greedy algorithm. Start with DP solution.
Define stayi, lefti and righti as maximal count of trees that woodcutters can fell, if only trees with number from 1 to i exist, and i-th tree isn't cutted down, i-th tree is cutted down and fallen left, i-th tree is cutted down and fallen right correspondingly. Now we can compute this values for each i from 1 to n by O(n) time because for each next we need only two previous value. Answer is maximum of stayn, leftn, rightn.
Also this problem can be solved by the next greedy algoritm. Let's fell leftmost tree to the left (it always doesn't make an answer worse). After that, try to fell the next tree. If we can fell it to the left, let's do it (because it also always doesn't make an answer worse). If we can't, then try to fell it to the right. If it is possible, let's do it. Last step is correct because felling some tree to the right may only prevent the next tree's fallen. So we may "exchange" one tree to another without worsing an answer.
Time complexity — O(n).
We can solve this problem by greedy algorithm. Let's prove that it is always possible find an answer (queue with the maximal number of not disappointed people), where all not disappointed people are at the begin of queue. Assume the contrary — there are two position i and j such that i < j, persons at position from i to j - 1 are disappointed, but j-th person isn't. Then just swap persons at positions i and j. After that all persons from i to j - 1 will be still disappointed (or become not disappointed) and j-th person will be still not disappointed. So the answer isn't maked worse.
So, we need to find person with minimal ti, that can be served now and will be not disappointed. We can do that by sorting all the people by time ti and try to serve them one by one. If somebody will be disappointed, we may send he to the end of queue, and doesn't add his serve time to the waiting time.
Time complexity — O(n + sort).
It's true, that Dijkstra modification, where in case of equal distances we take one with shorter last edge, find an answer.
For prove that let's do some transformation with graph. At first, find all shortest paths from u to other vertices. Define di as the length of shortest path from u to i. After that, we can delete some edges. Specifically, we can delete an edge with ends in x and y and weight w if |dx - dy| ≠ w, because it isn't contained in any shortest path, so it isn't contained in shortest path tree. After that, we can direct all edges from vertices with less distance to vertices with greater distance (because of all weight are positive). It's easy to prove, that if we take one edge that entering each vertex, we have a shortest path tree. Then we only need to take for each vertex minimal egde, that entering this vertex. Why? Because we have to take at least one edge, that entering each vertex to make a graph connected. We can't take edges with less weights than minimal. And if we take minimal edges, that entering each vertex we will have an shortest path tree. So that is minimal possible total wieght of shortest path tree.
You can see, that Dijkstra with modification do exactly the same things.
Time complexity —