A certain question on Quora and some junior asking about DP on Trees is what inspired this post. Its been a long time since I wrote any tutorial, so, its a welcome break from monotonicity of events.
Pre-requisites:
- Will to read this post thoroughly. :)
- Also, you should know basic dynamic programming, the optimal substructure property and memoisation.
- Trees(basic DFS, subtree definition, children etc.)
Dynamic Programming(DP) is a technique to solve problems by breaking them down into overlapping sub-problems which follow the optimal substructure. We all know of various problems using DP like subset sum, knapsack, coin change etc. We can also use DP on trees to solve some specific problems.
We define functions for nodes of the trees, which we calculate recursively based on children of a nodes. One of the states in our DP usually is a node i, denoting that we are solving for the subtree of node i.
As we do examples, things will get clear for you.
Problem 1
==============
The first problem we solve is as follows: Given a tree T of N nodes, where each node i has Ci coins attached with it. You have to choose a subset of nodes such that no two adjacent nodes(i.e. nodes connected directly by an edge) are chosen and sum of coins attached with nodes in chosen subset is maximum.
This problem is quite similar to 1-D array problem where we are given an array A1, A2, ..., AN; we can't choose adjacent elements and we have to maximise sum of chosen elements. Remember, how we define our state as 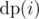 denoting answer for A1, A2, ..., Ai. Now, we define our recurrence as
denoting answer for A1, A2, ..., Ai. Now, we define our recurrence as 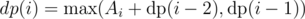 (two cases: choose Ai or not, respectively).
(two cases: choose Ai or not, respectively).
Now, unlike array problem where in our state we are solving for first i elements, in case of trees one of our states usually denotes which subtree we are solving for. For defining subtrees we need to root the tree first. Say, if we root the tree at node 1 and define our DP  as the answer for subtree of node V, then our final answer is
as the answer for subtree of node V, then our final answer is 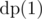 .
.
Now, similar to array problem, we have to make a decision about including node V in our subset or not. If we include node V, we can't include any of its children(say v1, v2, ..., vn), but we can include any grand child of V. If we don't include V, we can include any child of V.
So, we can write a recursion by defining maximum of two cases. .
.
As we see in most DP problems, multiple formulations can give us optimal answer. Here, from an implementation point of view, we can define an easier solution using DP. We define two DPs, 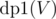 and
and 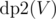 , denoting maximum coins possible by choosing nodes from subtree of node V and if we include node V in our answer or not, respectively. Our final answer is maximum of two case i.e.
, denoting maximum coins possible by choosing nodes from subtree of node V and if we include node V in our answer or not, respectively. Our final answer is maximum of two case i.e. 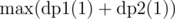 .
.
And defining recursion is even easier in this case.  (since we cannot include any of the children) and
(since we cannot include any of the children) and 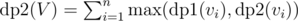 (since we can include children now, but we can also choose not include them in subset, hence max of both cases).
(since we can include children now, but we can also choose not include them in subset, hence max of both cases).
About implementation now. You must notice that answer for a node is dependent on answer of its children. We write a recursive definition of DFS, where we first call recursive function for all children and then calculate answer for current node.
//adjacency list
//adj[i] contains all neighbors of i
vector<int> adj[N];
//functions as defined above
int dp1[N],dp2[N];
//pV is parent of node V
void dfs(int V, int pV){
//for storing sums of dp1 and max(dp1, dp2) for all children of V
int sum1=0, sum2=0;
//traverse over all children
for(auto v: adj[V]){
if(v == pV) continue;
dfs(v, V);
sum1 += dp2[v];
sum2 += max(dp1[v], dp2[v]);
}
dp1[V] = C[V] + sum1;
dp2[V] = sum2;
}
int main(){
int n;
cin >> n;
for(int i=1; i<n; i++){
cin >> u >> v;
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(1, 0);
int ans = max(dp1[1], dp2[1]);
cout << ans << endl;
}
Complexity is O(N).
Problem 2:
==============
Given a tree T of N nodes, calculate longest path between any two nodes(also known as diameter of tree).
First, lets root tree at node 1. Now, we need to observe that there would exist a node x such that:
- Longest path starts from node x and goes into its subtree(denoted by blue lines in the image). Lets define by f(x) this path length.
- Longest path starts in subtree of x, passes through x and ends in subtree of x(denoted by red line in image). Lets define by g(x) this path length.
If for all nodes x, we take maximum of f(x), g(x), then we can get the diameter. But first, we need to see how we can calculate maximum path length in both cases.
Now, lets say a node V has n children v1, v2, ..., vn. We have defined f(i) as length of longest path that starts at node i and ends in subtree of i. We can recursively define f(V) as 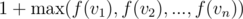 , because we are looking at maximum path length possible from children of V and we take the maximum one. So, optimal substructure is being followed here. Now, note that this is quite similar to DP except that now we are defining functions for nodes and defining recursion based on values of children. This is what DP on trees is.
, because we are looking at maximum path length possible from children of V and we take the maximum one. So, optimal substructure is being followed here. Now, note that this is quite similar to DP except that now we are defining functions for nodes and defining recursion based on values of children. This is what DP on trees is.
Now, for case 2, a path can originate from subtree of node vi, and pass through node V and end in subtree of vj, where i ≠ j. Since, we want this path length to be maximum, we'll choose two children vi and vj such that f(vi) and f(vj) are maximum. We say that  .
.
For implementing this, we note that for calculating f(V), we need f to be calculated for all children of V. So, we do a DFS and we calculate these values on the go. See this implementation for details.
If you can get the two maximum elements in O(n), where n is number of children then total complexity will be O(N), since we do this for all the nodes in tree.
//adjacency list
//adj[i] contains all neighbors of i
vector<int> adj[N];
//functions as defined above
int f[N],g[N],diameter;
//pV is parent of node V
void dfs(int V, int pV){
//this vector will store f for all children of V
vector<int> fValues;
//traverse over all children
for(auto v: adj[V]){
if(v == pV) continue;
dfs(v, V);
fValues.push_back(f[v]);
}
//sort to get top two values
//you can also get top two values without sorting(think about it) in O(n)
//current complexity is n log n
sort(fValues.begin(),fValues.end());
//update f for current node
f[V] = 1;
if(not fValues.empty()) f[V] += fValues.back();
if(fValues.size()>=2)
g[V] = 1 + fValues.back() + fValues[fValues.size()-2];
diameter = max(diameter, max(f[V], g[V]));
}
Now, we know the basics, lets move onto solving a little advanced problems.
Problem 3:
==============
Given a tree T of N nodes and an integer K, find number of different sub trees of size less than or equal to K.
First, what is a sub tree of a tree? Its a subset of nodes of original tree such that this subset is connected. Note a sub tree is different from our definition of subtree.
Always think by rooting the tree. So, say that tree is rooted at node 1. At this moment, I define S(V) as the subtree rooted at node V. This subtree definition is different from the one in problem. In S(V) all nodes in subtree of V are included.
Now, lets try to count total number of sub trees of a tree first. Then, we'll try to use same logic for solving original problem.
Lets define f(V) as number of sub trees of S(V) which include node V i.e. you choose V as root of the sub trees that we are forming. Now, in these subtrees, for each child u of node V, we have two options: whether to include them in sub tree or not. If you are including a node u, then there are f(u) ways, otherwise there is only one way(since we can't choose any nodes from S(u), otherwise the subtree we are forming will get disconnected).
So, if node V has children v1, v2, ..., vn, then we can say that 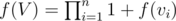 . Now, is our solution complete? f(1) counts number of sub trees of T which are rooted at 1. What about sub trees which are not rooted at 1? We need to define one more function g(V) as number of subtrees of S(V) which are not rooted at V. We derive a recursion for g(V) as
. Now, is our solution complete? f(1) counts number of sub trees of T which are rooted at 1. What about sub trees which are not rooted at 1? We need to define one more function g(V) as number of subtrees of S(V) which are not rooted at V. We derive a recursion for g(V) as 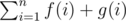 i.e. for each child we add to g(V) number of ways to choose a subtree rooted at that child or not rooted at that child.
i.e. for each child we add to g(V) number of ways to choose a subtree rooted at that child or not rooted at that child.
Our final answer is f(1) + g(1).
Now, onto our original problem. We are trying to count sub trees of T whose size doesn't exceed K. We need to have one more state in our DP at each node. Lets define f(V, k) as number of sub trees with k nodes and V as root. Now, we can define recurrence relation for this. Let's say for node V, there are direct children nodes v1, v2, ..., vn. Now, to form a subtree with k + 1 nodes rooted at V, lets say S(vi) contributes ai nodes. Of course, k must be 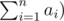 since we are forming a sub tree of size k + 1(one node is contributed by V). We should realise that f(V, k) is sum of the value
since we are forming a sub tree of size k + 1(one node is contributed by V). We should realise that f(V, k) is sum of the value 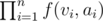 for all possible distinct sequences a1, a2, ..., an.
for all possible distinct sequences a1, a2, ..., an.
Now, to do this computation at node V, we will form one more DP denoted by 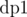 . We say
. We say 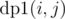 as number of ways to choose a total of j nodes from subtrees defined by v1, v2, ..., vi. The recurrence can be defined as
as number of ways to choose a total of j nodes from subtrees defined by v1, v2, ..., vi. The recurrence can be defined as 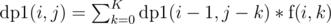 , i.e. we are iterating over k assuming that subtree of vi contributes k nodes.
, i.e. we are iterating over k assuming that subtree of vi contributes k nodes.
So, finally 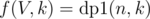 .
.
And our final solution is sum 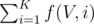 for all nodes V.
for all nodes V.
So, in terms of pseudo code we write:
f[N][K+1]
void rec(int cur_node){
f[cur_node][1]=1
for(all v such that v is children of cur_node)
rec(v)
dp_buffer[K] = {0}
for i=0 to K:
for j=0 to K-i:
dp_buffer[i + j] += f[v][i]*f[v][j]
f[cur_node] = dp_buffer
}
Now, lets analyse complexity. At each node with n children, we are doing a computation of n * K2, so total complexity is O(N * K2).
Another similar problem is : We are given a tree with N nodes and a weight assigned to each node, along with a number K. The aim is to delete enough nodes from the tree so that the tree is left with precisely K leaves. The cost of such a deletion is the sum of the weights of the nodes deleted. What is the minimum cost to reduce to tree to a tree with K leaves? Now, think about the states of our DP. Derive a recurrence. Before actually proceeding to the solution give it atleast a good thinking. Find solution here.
Problem 4:
==============
Given a tree T, where each node i has cost Ci. Steve starts at root node, and navigates to one node that he hasn't visited yet at random. Steve will stop once there are no unvisited nodes. Such a path takes total time equal to sum of costs of all nodes visited. What node should be assigned as root such that expected total time is minimised?
First, lets say tree is rooted at node 1, then we calculate total expected time for the tree formed. We define f(V) as expected total time if we start at node V and visit in subtree of V. If V has children v1, v2, ..., vn, we can say that 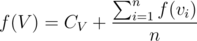 , since with same probability we'll move down each of the children.
, since with same probability we'll move down each of the children.
Now, we have to find a node v such that if we root tree at v, then f(v) is minimised. Now, f(v) is dependent on where we root the tree. If we do a brute force, it'll be O(N2). We need faster than this to pass.
We'll try to iterate over all nodes V and quickly calculate the value of f(V) if tree is rooted at V. We need to see the contribution of 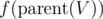 if tree is rooted at V. We already know the contribution of children of V. So, if we define one more quantity g(V) as the expected total time at node
if tree is rooted at V. We already know the contribution of children of V. So, if we define one more quantity g(V) as the expected total time at node 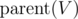 , if we don't consider contribution of subtree of V.
, if we don't consider contribution of subtree of V.
Now, if I want to root my whole tree at V, then total expected time at this node will be 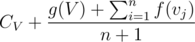 . To realise this is correct, have a look at definition of g(V).
. To realise this is correct, have a look at definition of g(V).
Lets see how we can calculate g(V). Keep referring to image below this paragraph while reading. Consider a node p which has parent p' and children v1, v2, ..., vn. Now, lets try to find g(vi). g(vi) means root tree at node p and don't consider subtree of vi for calculating f(p). We can say that 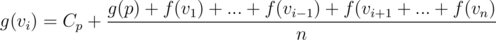 , since g(p) gives us the expected total time at p' without considering subtree of p. We divide by n, because p will have n children i.e. p', v1, ..., vi - 1, vi + 1, ..., vn.
, since g(p) gives us the expected total time at p' without considering subtree of p. We divide by n, because p will have n children i.e. p', v1, ..., vi - 1, vi + 1, ..., vn.
We can calculate both functions f and g recursively in O(N).
Problem 5:
==============
Another very interesting problem goes as: Given two rooted trees T1 and T2, you want to make T1 as structurally similar to T2. For doing that you can insert leaves one by one in any of the trees. You have to tell the minimum number of insertions required to do so.
Lets say both trees are rooted at nodes 1. Now, say T11 has children u1, u2, ..., un and T21 has children v1, v2, ..., vm, then we are going to create a mapping between nodes in set u and v i.e. we are going to make subtree of some node ui exactly same as vj, for some i, j, by adding required nodes. If n ≠ m, then we are going to add the whole subtree required.
Now, how do we decide which node in T1 is mapped to which in T2. Again, we use DP here. We define 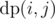 as minimum additions required to make subtree of node i in T1 similar to subtree of node j in T2. We need to come up with a recurrence.
as minimum additions required to make subtree of node i in T1 similar to subtree of node j in T2. We need to come up with a recurrence.
Lets say node i has children u1, u2, ..., un and node j has children v1, v2, ..., vm. Now, if we assign node ui with node vj, then the cost is going to be 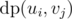 . Now, to all nodes in u, we have to assign nodes from v such that total cost is minimised. This can be solved by solving assignment problem. In assignment problem there is a cost matrix C, where C(i, j) denotes cost if task i is assigned to person j. Our aim is to assign one task to one person such that total cost is minimised. This can be done in O(N3), if there are N tasks. Here in our problem
. Now, to all nodes in u, we have to assign nodes from v such that total cost is minimised. This can be solved by solving assignment problem. In assignment problem there is a cost matrix C, where C(i, j) denotes cost if task i is assigned to person j. Our aim is to assign one task to one person such that total cost is minimised. This can be done in O(N3), if there are N tasks. Here in our problem  and by solving this assignment problem, we can get value of
and by solving this assignment problem, we can get value of 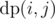 .
.
Total complexity of this solution is O(N3), where N is maximum number of nodes in T1 and T2.
That's the end of it. Now time for some person advice :) The more you practice DP/DP on trees, the more comfortable you are going to be. So, get on your practice shoes and run over the obstacles! There are lot of DP on trees problem which you can try to solve and if you don't get the solution look at the tutorial/editorial, if you still don't get solution ask on various platforms.
Problems for practice:
1 2 3 4 5 6 7 (Solution for 7) 8 9 10 11 12 13






