620A - Professor GukiZ's Robot
Easy to see that the answer is max(|x1 - x2|, |y1 - y2|).
Complexity: O(1).
620B - Grandfather Dovlet’s calculator
Let's simply iterate over all the values from a to b and add to the answer the number of segments of the current value x. To count the number of segments we should iterate over all the digits of the number x and add to the answer the number of segments of the current digit d. These values can be calculated by the image from the problem statement and stored in some array in code.
Complexity: O((b - a)logb).
620C - Pearls in a Row
Let's solve the problem greedily. Let's make the first segment by adding elements until the segment will be good. After that let's make the second segment in the same way and so on. If we couldn't make any good segment then the answer is - 1. Otherwise let's add all uncovered elements at the end to the last segment. Easy to prove that our construction is optimal: consider the first two segments of the optimal answer, obviously we can extend the second segment until the first segment will be equal to the first segment in our construction.
Complexity: O(nlogn).
620D - Professor GukiZ and Two Arrays
We can process the cases of zero or one swap in O(nm) time. Consider the case with two swaps. Note we can assume that two swaps will lead to move two elements from a to b and vice versa (in other case it is similar to the case with one swap). Let's iterate over all the pairs of the values in a and store them in some data structure (in C++ we can user map). Now let's iterate over all the pairs bi, bj and find in out data structure the value v closest to the value x = sa - sb + 2·(bi + bj) and update the answer by the value |x - v|. Required sum we can find using binary search by data structure (*map* in C++ has lower_bound function).
Сложность: O((n2 + m2)log(n + m)).
620E - New Year Tree
Let's run dfs on the tree and write out the vertices in order of their visisiting by dfs (that permutation is called Euler walk). Easy to see that subtree of any vertex is a subsegment of that permutation. Note that the number of different colours is 60, so we can store the set of colours just as mask of binary bits in 64-bit type (*long long* in C++, long in Java). Let's build the segment tree over the permutation which supports two operations: paint subsegment by some colour and find the mask of colours of some segment.
Complexity: O(nlogn).
620F - Xors on Segments
We gave bad constraints to this problem so some participants solved it in O(n2 + m) time.
Note that 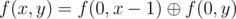 . The values f(0, x) can be simply precomputed. Also you can notice that the value f(0, x) is equal to x, 1, x + 1, 0 depending on the value x modulo 4.
. The values f(0, x) can be simply precomputed. Also you can notice that the value f(0, x) is equal to x, 1, x + 1, 0 depending on the value x modulo 4.
Let's use Mo's algorithm: we should group all the queries to  blocks by the left end and sort all the queries in each block by the right end. Let r be the maximal left end inside the current group then all left ends will be in distance not greater than
blocks by the left end and sort all the queries in each block by the right end. Let r be the maximal left end inside the current group then all left ends will be in distance not greater than  from r and right ends will be in nondecreasing order, so we can move the right end by one (total we will made no more than n movements in each block). During moving of the right end inside some group from the value r + 1 to the value of the current right end we will maintain two tries: the first for the values f(0, x - 1) and the second for the values f(0, x), in the first we will maintain the minimal value of x, in the second — the maximal. After adding some values to the trie we should find the maximal value that can be formed by the current value x. To do that we should go down in the first trie maintaining the invariant that in the current subtree the minimal value is not greater than x. Each time we should go by the bit that is not equal to the corresponding bit in x (if we can do that, otherwise we should go by the other bit). In the second trie we should do the same thing with the difference that we should maintain the invariant that the maximal value in the current subtree is not less than the value x. After moving the right end we should iterate from the left end of the query to r and update the answer (without adding the current value to the tries). Also after that all we should iterate over all the queries and with new empty tries iterate from the left end to r, add the current values to the tries and update the answer.
from r and right ends will be in nondecreasing order, so we can move the right end by one (total we will made no more than n movements in each block). During moving of the right end inside some group from the value r + 1 to the value of the current right end we will maintain two tries: the first for the values f(0, x - 1) and the second for the values f(0, x), in the first we will maintain the minimal value of x, in the second — the maximal. After adding some values to the trie we should find the maximal value that can be formed by the current value x. To do that we should go down in the first trie maintaining the invariant that in the current subtree the minimal value is not greater than x. Each time we should go by the bit that is not equal to the corresponding bit in x (if we can do that, otherwise we should go by the other bit). In the second trie we should do the same thing with the difference that we should maintain the invariant that the maximal value in the current subtree is not less than the value x. After moving the right end we should iterate from the left end of the query to r and update the answer (without adding the current value to the tries). Also after that all we should iterate over all the queries and with new empty tries iterate from the left end to r, add the current values to the tries and update the answer.
С++ solution: in this code the trie number 0 corresponds to the second trie and the trie number 1 corresponds to the first trie.
Complexity: 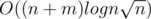 .
.







