798A - Mike and palindrome
Let cnt be the number of 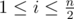 such that si ≠ sn - i + 1.
such that si ≠ sn - i + 1.
If cnt ≥ 2 then the answer is NO since we must change more than 1 character.
If cnt = 1 then the answer is YES.
If cnt = 0 and n is odd answer is YES since we can change the character in the middle, otherwise if n is even the answer is NO because we must change at least one character.
Complexity is O(|s|).
Solution: Link
798B - Mike and strings
First of all, you must notice that the operation of removing the first character and appending it to the left is equivalent to cyclically shifting the string one position to the left.
Let's denote by dpi, j the smallest number of operations for making the first i strings equal to string si moved j times.
Let f(i, j) be the the string si moved j times,then 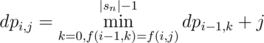 .
.
The answer is min(dpn, 0, dpn, 1, ..., dpn, |sn| - 1).
The complexity is O(|S|3 × n).
Solution: Link
798C - Mike and gcd problem
First of all, the answer is always YES.
If 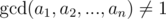 then the answer is 0.
then the answer is 0.
Now suppose that the gcd of the sequence is 1. After we perform one operation on ai and ai + 1, the new gcd d must satisfy d|ai - ai + 1 and d|ai + ai + 1  d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
d|2ai and d|2ai + 1. Similarly, because d is the gcd of the new sequence, it must satisfy d|aj, j ≠ i, i + 1.
Using the above observations we can conclude that  , so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
, so the gcd of the sequence can become at most 2 times bigger after an operation. This means that in order to make the gcd of the sequence bigger than 1 we need to make all numbers even. Now the problem is reduced to the following problem:
Given a sequence v1, v2, ... , vn of zero or one,in one move we can change numbers vi, vi + 1 with 2 numbers equal to 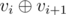 . Find the minimal number of moves to make the whole sequence equal to 0.
. Find the minimal number of moves to make the whole sequence equal to 0.
It can be proved that it is optimal to solve the task for consecutive ones independently so we divide the array into the minimal number of subarrays full of ones, if their lengths are s1, s2, ... , st,the answer is  .
.
Complexity is 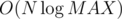 .
.
Solution: Link
798D - Mike and distribution
In the beginning, it's quite easy to notice that the condition " 2·(ap1 + ... + apk) is greater than the sum of all elements in A " is equivalent to " ap1 + ... + apk is greater than the sum of the remaining elements in A ".
Now, let's store an array of indices C with Ci = i and then sort it in decreasing order according to array A, that is we must have ACi ≥ ACi + 1.
Our answer will always have size 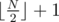 . First suppose that N is odd. Add the first index to our set, that is make p1 = C1. Now, for the remaining elements, we will consider them consecutively in pairs. Suppose we are at the moment inspecting AC2k and AC2k + 1. If BC2k ≥ BC2k + 1 we make pk + 1 = C2k, else we make pk + 1 = C2k + 1.
. First suppose that N is odd. Add the first index to our set, that is make p1 = C1. Now, for the remaining elements, we will consider them consecutively in pairs. Suppose we are at the moment inspecting AC2k and AC2k + 1. If BC2k ≥ BC2k + 1 we make pk + 1 = C2k, else we make pk + 1 = C2k + 1.
Why does this subset work? Well, it satisfies the condition for B because each time for consecutive non-intersecting pairs of elements we select the bigger one, and we also add BC1 to the set, so in the end the sum of the selected elements will be bigger than the sum of the remaining ones.
It also satisfies the condition for A, because Ap1 is equal or greater than the complement element of p2 (that is — the index which we could've selected instead of p2 from the above procedure — if we selected C2k then it would be C2k + 1 and vice-versa). Similarly Ap2 is greater than the complement of p3 and so on. In the end we also add the last element from the last pair and this makes the sum of the chosen subset strictly bigger than the sum of the remaining elements.
The case when N is even can be done exactly the same as when N is odd, we just pick the last remaining index in the end.
The complexity is 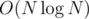 .
.
Solution: Link
798E - Mike and code of a permutation
Let's consider ai = n + 1 instead of ai = - 1. Let's also define the sequence b, where bi = j such that aj = i or bi = n + 1 if there is no such j. Lets make a directed graph with vertices be the indices of the permutation p with edges of type (a, b) representing that pa > pb. If we topologically sort this graph then we can come up with a possible permutation: if S is the topologically sorted graph then we can assign to pSi number i.
In this problem we will use this implementation of topological sort.
But how we can find the edges? First of all there are edges of the form (i, bi) if bi ≠ n + 1 .For a vertex i he visited all the unmarked vertices j (1 ≤ j < ai, j ≠ i) and you know for sure that for all these j, pj < pi. But how we can check if j was already marked? The vertex j will become marked after turn of vertex bj or will never become unmarked if bj = n + 1. So there is a direct edge from i to j if j = bi or 1 ≤ j < ai, j ≠ i and bj > i.
Suppose we already visited a set of vertices and for every visited vertex node we assigned to bnode value 0 (for simplicity just to forget about all visited vertices) and now we want to find quickly for a fixed vertex i an unvisited vertex j with condition that there is edge (i, j) or say it there isn't such j, if we can do that in subquadratic time then the task is solved. As stated above the first condition is j = bi if 1 ≤ bi ≤ n, this condition is easy to check. The second condition is 1 ≤ j < ai and bj > i, now consider vertices with indices from interval 1..ai - 1 and take j with maximal bj. If bj > i we found edge (i, j) otherwise there are no remaining edges. We can find such vertex j using segment tree and updating values while we visit a new vertex. In total we will visit n vertices and query the segment tree at most 2 × (n - 1) times (n - 1 for every new vertex and n - 1 for finding that there aren't remaining edges).
Complexity and memory are 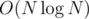 and O(N).
and O(N).
Solution: Link





