Hello, codeforces!
Sorry for the long break, but the last weeks of holidays and the first weeks of academic year took my attention. I hope today's trick will make you forgive me. :P
I invented this trick a few years ago, but for sure I wasn't first, and some of you already know it. Let's consider the following interactive task. There are n (1 ≤ n ≤ 105) hidden integers ai, each of them from range [1, 1018]. You are allowed to ask at most 103000 queries. In one query you can choose two integers x and y (1 ≤ x ≤ n, 1 ≤ y ≤ 1018) and ask a question ''Is ax ≥ y?'' The task is to find the value of the greatest element in the hidden array. The checker isn't adaptive.
Unfortunately, this task is only theoretical, and you cannot solve it anywhere, but it'll turn out, that solution can be handy in many other, much more complicated problems.
Even beginners should be able to quickly come up with a solution which asks n·log(d) queries (where d = 1018). Unfortunately, this is definitely too much. The mentioned solution, of course, does n independent binary searches, to find each ai.
Some techniques come to mind, for example we could do all binary searches at the same time, ask for each element if it's greater than  , or something, then forget about lower values... but no, things like that would aim only at really weak, random test cases. More, it seems that they wouldn't work on a first random max-test.
, or something, then forget about lower values... but no, things like that would aim only at really weak, random test cases. More, it seems that they wouldn't work on a first random max-test.
The limit on the number of queries slightly higher than the limit on n should give us a hint: for many elements of the array, we should ask about them only once (of course we have to ask about each of them at least once). So, maybe let's develop a solution which at least has a chance to do it. Here comes an idea: let's iterate over numbers in the hidden array like in the n·log(d) solution, but before doing the binary search, ask if ai that we are looking at right now is strictly greater than the greatest value that we've already seen. It is isn't, there is no point in doing the binary search here — we are only interested in greatest value.
Of course, this solution can do the binary search even n times, for example when the hidden array is increasing. Here comes a key idea: let's consider numbers in random order! It would definitely decrease the number of binary searches that we would do, but how much? Let's consider the following example (and assume that numbers are already shuffled):
10, 14, 12, 64, 20, 62, 59, 39, 57, 96, 37, 91, 88, 5, 76
A filled circle means that we do the binary search, an empty circle means that we skip this number.
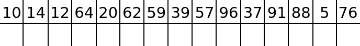
Of course, we should do the binary search when the prefix maximum changes (increases, in particular, it can't decrease). How many times will it happen on average? Let's focus on the global maximum. It's clear that for sure we have to do the binary search to find its exact value and that we won't do binary search anymore to its right. What with elements to its left? The situation turns out to be analogical. Where will be the global maximum in a shuffled array? Somewhere in the middle, won't it? So, we'll do the last binary search in the middle (on average), one before last in the middle of the left (on average again) half and so on. Now, it's easy to see that we'll do the binary search only O(log(n)) times! A total number of queries will be equal to n + O(log(n)·log(d)), which seems to be enough. It also can be proven or checked with DP/Monte Carlo, that probability that the number of binary searches will be high is very low.
OK, nice task, randomized solution, but how could it be useful in other problems? Here's a good example: 442E - Gena and Second Distance. Editorial describes the solution, so I'll mention only the essence. We want to maximize some result, and we have n ''sources'' that we can take the result from. In each of them we do the binary search to find the highest possible result from this source, and then we print the maximum of them. Looks familiar? The most eye-catching difference is that in this task we have to deal with real numbers.
Experience tells me that this trick is in most cases useful in geometry. It also reminds me how I discovered this trick: when I was solving a geometry problem in high school and trying to squeeze it in the time limit. I decided to check if current ''source'' will improve my current result and if not — to skip the binary search. It gave me many more points (it was an IOI-like problem) even without shuffling sources. Why? Test cases were weak. :D
So, did another blog about randomization satisfy your hunger? If you know more problems which could be solved with this trick, share them in the comments. See you next time! :D






