| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
Hello, Codeforces!
Zlobober and I are glad to invite you to compete in Nebius Welcome Round (Div. 1 + Div. 2) that will start on 12.03.2023 17:35 (Московское время). The round will be rated for everyone and will feature 8 problems that you will have 2 hours to solve.
I feel really thrilled and excited about this round as this is the first time I put so much effort in a Codeforces contest since I quit being a round coordinator in December 2016 (wow, that was so long ago)!
We conduct this round to have some fun and we also hope to find some great candidates to join Nebius team. Solving 5+ problems in our round will be a good result and will count as one of the coding interviews. Apart from that top 25 contestants and 25 random contestants placed 26-200 will receive a branded Nebius t-shirt!

Some information about Nebius. I have joined this new start-up in cloud technologies in November as a head of Compute & Network Services. It's an international spin-off of Yandex cloud business with offices in Amsterdam, Belgrade and Tel Aviv. We offer strategic partnerships to leading companies around the world, empowering them to create their own local cloud hyperscaler platforms and become trustworthy providers of cloud services and technologies in their own regions.
We know that competitive programming makes great engineers. It boosts your algorithms and coding skills, teaches you to write a working and efficient code. We aim to hire a lot of backend software engineers for all parts of our cloud technology stack that ranges from hypervisor and network to data warehouse and machine learning.
Here you can check Nebius website and open positions. If you feel interested in joining Nebius as a full-time employee, go on and fill the form.
Special thanks go to:
MikeMirzayanov for his outstanding, glorious, terrific (you can't say enough, really) platforms Codeforces and Polygon
74TrAkToR and KAN for this round coordination (and for rounds coordination in general, good job lads!)
ch_egor for his help with one of the problem that has a peculiar setting which we will discuss a lot in the editorial
UPD Now that the list is complete we can say many thanks to all the testers! dario2994, errorgorn, magga, golikovnik, Hyperbolic, Farhan132, IgorI, vintage_Vlad_Makeev, aymanrs, Vladik, Junco_dh, dshindov, csegura, Eddard, Alexdat2000, kLOLik, wuruzhao, Aleks5d, Ryougi-Shiki, qrort, ak2006, AsGreyWolf, farmerboy, vladukha, usernameson, segment_tea, DzumDzum, Java, samvel, qwexd, Tensei8869, thank you for all your help on improving this round's quality!
Fingers crossed all will be well, you will enjoy the round and we will be back with a new one in several months!
UPD2 The scoring distribution is 500 — 1000 — 1000 — 1500 — 2000 — 2750 — 3500 — 3500.
UPD3 The editorial is here!
UPD4 Congratulations to winners!
1-st place: jiangly
2-nd place: tourist
3-rd place: Um_nik
4-th place: isaf27
5-th place: Ormlis
UPD5 T-shirts winners!
Smart Vending
Problem idea and development: GlebsHP.
First we observe that Arcadiy won't be able to spend more money than he has, i.e. the number of bottles he can buy doesn't exceed  . However, it might happen that Arcadiy won't be able to buy exactly this number because he won't have enough coins to buy next bottle with no change and the machine won't possess enough coins to give change if Arcadiy tries to pay with banknotes only.
. However, it might happen that Arcadiy won't be able to buy exactly this number because he won't have enough coins to buy next bottle with no change and the machine won't possess enough coins to give change if Arcadiy tries to pay with banknotes only.
Note that the total number of coins doesn't change and is always c + d. Moreover, if c + d ≥ 999 999, then either Arcadiy will always have enough coins to buy a bottle with no change, or machine will have enough coins to give a change. In this case the answer is z.
If c + d < 999 999, then it can be the case that Arcadiy has enough coins to buy bottle with no change, it can be the case that machine has enough coins to give change, but it can't be the case that both is possible. That means we can simulate the process but that might work tool long.
Denote as ai the number of coins Arcadiy has after first i moves (a0 = c). Note that if ai = aj, then ai + 1 = aj + 1 (indeed, the way to buy next bottle is uniquely defined by value ai) and the sequence repeats itself. We will simulate the process of buying Kvas-Klass bottle by bottle till we find some value of ai that we already met or it is not possible to make next purchase. In case ai repeats the answer is z, otherwise the answer is the number of step when the next purchase was not possible.
Exercise: solve the task if one banknote is 1012 rubles.
LIS vs. LDS
Problem idea and development: Endagorion.
Let us draw n points pi = (i, ai) in the plane. Let I = (i1, ..., ik) and J = (j1, ..., jl) be a pair of non-intersecting LIS and LDS. From maximality of I, there can be no points strictly inside the following rectangles (described by their opposite corners):
A0 = ((0, 0), pi1);
Ax = (pix, pix + 1) for all 1 ≤ x < k;
Ak = (pik, (n + 1, n + 1)).
Similarly, since J is maximal, there can be no points inside these rectangles:
B0 = ((0, n + 1), pj1);
By = (pjy, pjy + 1) for all 1 ≤ y < l;
Bl = (pjl, (n + 1, 0)).
These two chains of rectangles connect the opposite corners of the square ((0, 0), (n + 1, n + 1)). Assuming that I and J do not intersect, there must be an intersecting pair of rectangles Ax and By. None of Ax and By contains any points, hence there are only two cases how they can intersect:
ix < jy < jy + 1 < ix + 1, ajy + 1 < aix < aix + 1 < ajy (as in the first sample);
jy < ix < ix + 1 < jy + 1, aix < ajy + 1 < ajy < aix + 1 (the mirror image of the previous option).
We will try to look for possible intersections of type 1 (the other one can be found similarly after reversing the whole permutation). Let's say that (i, i') is an {\it LIS-pair} if a and b are consecutive elements of an LIS ({\it LDS-pair} is defined similarly). Suppose that there is an LIS-pair (i, i') and an LDS-pair (j, j') such that i < j < j' < i' and aj' < ai < ai' < aj, that is, there is an intersection of type 1 between certain LIS and LDS. This means that we can find an answer by constructing all LIS- and LDS-pairs and looking for such intersection.
Of course, there are too many possible pairs. However, notice that in the situation above we can replace i' with 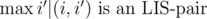 , and j' with
, and j' with 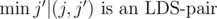 . This means that we will only consider O(n) pairs to intersect. Among these, finding an intersection can be done with a sweep-line approach that uses segment tree.
. This means that we will only consider O(n) pairs to intersect. Among these, finding an intersection can be done with a sweep-line approach that uses segment tree.
Eat And Walk
Problem idea and development: GlebsHP.
To start with we consider the minor change in the problem: let the initial movements be free and the movements after x units of food cost x per 1 move left or right. One can show that the optimal strategy is to reach some position x and then move only in the direction of position 0, visiting some of the restaurants. If we visit restaurant i the weight increases by ai and each move costs ai more. Assuming we only move left after visiting any restaurants we can say that visiting restaurant i costs ai·i units of energy in total.
Now we have a knapsack problem with n items, the i-th of them has weight ai·i and cost ai, the goal is to find a subset of maximum total cost and total weight not exceeding e. Standard solution is to compute dynamic programming d(i, x) — maximum possible total cost if we select among first i items and the total weight is equal to x.
Now we swap parameter and value of dynamic programming and compute d(i, c) — minimum possible total weight that the subset of cost c selected among first i items can have. Then we are going to add items in order of descending i, so value d(i, c) will be composed using elements from i-th to n-th. What are the values of c to consider? Each unit of cost (food in original terms) that comes from restaurants with indices i and greater requires at least i units of energy so we should only consider values of 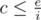 . Using the formulas to estimate harmonic series we can say that we only need to compute
. Using the formulas to estimate harmonic series we can say that we only need to compute 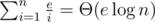 elements of dynamic programming.
elements of dynamic programming.
To finish the solution we should count the initial cost to move to maximum index restaurant we visit (and back). Let this index be k, we should increase answer by 2k. This can be done by using extra cost in dynamic programming when we consider moves from state d(i, 0).
Search Engine
Problem idea: GlebsHP. Development: cdkrot.
Let's notice, that in the end, after prepending and appending of all letters, Alice will have string s exactly.
Suppose, that we were adding new letters and having at least one occurrences inside s, and then added one symbol and all the occurrences disappeared. In that case, the all following additions have zero occurrences count and we should have stopped on that bad step, selected one of occurrences and then growed it to the left and to the right to the bounds of s.
Because of this observation, we can reverse the process: let's say that initially we have string s, and then we are allowed to delete the letters from left or right side, with the same goal to maximize the total number of occurrences.
Let's build a suffix tree on s, which is a trie with all suffixes of s.
Then we can do a dynamic programming on the vertices of the suffix tree. Let's denote dp[v] as the maximum sum which we can achieve if we start with string, which corresponds to the path from root to v and repeatedly deleted letters from left or right, counting the total number of occurrences in the whole string s.
This dynamic programming has only two transitions — we can go to the parent vertex (which corresponds to deletion of the last letter), or go by the suffix link (which corresponds to deletion of the first letter). We can calculate this dynamic programming lazily and the number of occurrences of the string is simply the number of terminal vertices in it's subtree (this can be calculated for all vertices beforehand).
However, this way we have n2 states in our dynamic programming, so we will have to use the compressed suffix tree.
In compressed suftree, transition to the parent may mean deletion of multiple symbols on the suffix. In this case, number of occurrences anywhere between the edge is equal to the number of occurrences of the lower end (so you need to multiply it by the edge length). The same also holds for the suffix links transitions.
The only thing we missed, it that the optimal answer could have transitions up by one symbol and suffix links transitions interleaved, and we can't simulate this with compressed suffix tree. However, one never needs to interleave them. Assume, that in optimal answer we were going up and then decided to go by suffix link and finish the edge ascent after it. In that case we can simply go by the suffix link first and traverse the edge after that — this way the total number of occurrences can only increase.
The complexity is  , also the problem can be solved with the suffix automaton and dynamic programming on it. In that case, the dynamic transitions are suffix links and reverse edges.
, also the problem can be solved with the suffix automaton and dynamic programming on it. In that case, the dynamic transitions are suffix links and reverse edges.
Exercise: solve the problem if the game starts from some substring (defined by li and ri) and you need to process up to 100 000 queries.
Guess Me If You Can
Problem idea and development: GlebsHP.
Note that if we name all elements in some order, at the end we will have position similar to the initial but shifted by 1. This shift doesn't affect neither answer, nor intermediate values returned by interactor.
Consider some triple of elements i, j and k such that pi + 1 = pj = pk - 1. In case we list elements in some order such that j goes before i and k, in the moment pj is increased by 1 the number of distinct element decreases and we can say that position j doesn't contain maximum.
What if we select a random permutation and name all elements in this order. For triple i, j, k we have chance  that j will go before i and k. Thus, if we use 50 random permutations, the probability to fail to find out that j is not a maximum is only
that j will go before i and k. Thus, if we use 50 random permutations, the probability to fail to find out that j is not a maximum is only 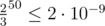 . The events corresponding to separate triples might not be independent so we estimate the probability to make at least one mistake as 2·10 - 9·n ≤ 2·10 - 6.
. The events corresponding to separate triples might not be independent so we estimate the probability to make at least one mistake as 2·10 - 9·n ≤ 2·10 - 6.
Lazy Hash Table
Problem idea: GlebsHP. Development: Arterm.
Note that 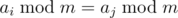 if and only if m|ai - aj. So, we have to find minimal m that doesn't divide any of differences ai - aj.
if and only if m|ai - aj. So, we have to find minimal m that doesn't divide any of differences ai - aj.
First find all possible values of d = ai - aj. Set
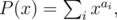
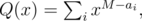
where M = max ai. Find product T(x) = P(x)·Q(x) using Fast Fourier Transform. As

coefficient with xM + d is nonzero if and only if there are i, j with ai - aj = d.
Now for each m in range [1, M] check if there is difference divisible by m. We can check this checking 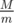 numbers:
numbers:  . So total complexity for this part is
. So total complexity for this part is 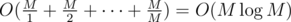 .
.
Overall complexity is  , где M = max ai ≤ 2 000 000.
, где M = max ai ≤ 2 000 000.
In case you want to take part in Yandex.Algorithm 2018 but somehow haven't registered yet, you might want to follow this link.
Qualification round has started at 00:00 Moscow time, February 17th. Round is a virtual competition 100 minutes long. You can start it at any moment of time till 23:59 on Sunday, February 18th (Moscow time).
We recall that in order to be able to participate in elimination stage one needs to accept at least one problem at qualification round. However, everyone who managed to accept at least one problem during warm-up has already qualified to the next stage.
Judges ask all the participant to withdraw from any problem discussion and do not publish any solutions till 01:40, February 19th.
Good luck, we hope that you will enjoy the problems!
A. Time Through the Glass
Consider the movement of "real" and "reflected" hands. If "real" hands rotates for some angle, "reflected" hand passes exactly the same angle in other direction. Thus, the sum of angles of two hands is always equal 360 degrees. For each hand we will find its resulting position independently. For hour hand it is 12 minus the current position, while for minute hand it is 60 minus current position. In both cases we should not forget to replace 12 or 60 with 0.
B. Palindromic Feature
Consider some substring of the given string that is a palindrome. We can remove its first character and its last character and the string will remain a palindrome. Continue this process till the string length becomes two or three (depending on parity).
The number of substrings of length two or three is linear, same as their total length. Thus, we can apply naive algorithm to select optimum palindrome. If there is no palinromic substring of length two or three, print - 1.
C. Divide Them All
To solve this problem we will use a simple geometry fact that a line split a circle in two parts of equal area if and only if this line passes through the circle center. Similarly, a line splits a rectangle in two parts of equal area if and only if it passes through the intersection point of its diagonals. In both cases, sufficiency follows from point symmetry and necessity can be shown by considering a line that passes through the center and is parallel to a given one.
Now we only need to check whether there exists a line that contains all the centers. For the sake of simplicity we will work with doubled coordinates to keep them integer. This allows us to get the center of the rectangle by computing the sum of coordinates of two opposite vertices.
If there are no more than two distinct points among the set of all center, the answer is definitely positive. Otherwise, consider any pair of distinct points and check that each center belongs to the line they define. To check whether three points a, b and c (a ≠ b) belong to one line we can compute the cross product of vectors b - a and c - a. Overall complexity of this solution is O(n).
D. Interview Task
We would like to start with some lemmas.
Lemma 1. Any two neighboring integers are co-prime at any step.
Use math induction. Base case is trivial as 1 and 1 are co-prime. Consider the statement is correct for first n steps. Then, any integer produced during step n + 1 is a sum of two co-prime integers. However, gcd(a + b, b) = gcd(a, b), thus, any two neighbors are still co-prime.
Lemma 2. Each ordered pair of integers (a, b) appears as neighbors exactly once (and at one step only).
Proof by contradiction. Let k be the first step such that some ordered pair appeared for the second time. Denote this pair as (p, q) and i ≤ k is the step of another appearance o this pair. Without loss of generality let p > q, then p was obtained as a sum of p - q and q, thus during the steps i - 1 and k - 1 there was also a repetition of some pair, that produces a contradiction.
Lemma 3. Any ordered pair of co-prime integers will occur at some step.
Let p and q be neighbors at some step. Then, if p > q it was obtained as a sum of p - q and q, so they were neighbors on the previous step. Two steps behind we had either p - 2q and q, or p - q and 2q - p (depending on which is greater, p - q or q) and so one. The process is similar to Euclid algorithm and continues while we don't have 1 and x. Finally, pairs (1, x) and (x, 1) always appear at step x$. Moving along the actions in backward direction we conclude that any of the intermediate pairs should appear during the process, thus, pair (p, q) also appears.
Notice, that we are only interested in the first n steps, as any integer, produced on step x is strictly greater than x. Now, as we know that any pair of co-prime integers occurs exactly once we would like to compute the number of pairs (p, q) such that gcd(p, q) = 1 and p + q = n. if gcd(p, q) = 1, then gcd(p, p + q) = gcd(p, n) = 1. It means we only have to compute Euler function of integer n.
Compute Euler function is a well-studied problem. This know this is a multiplicative function, so n = p1k1·p2k2·...·pnkn, the number of co-prime integers is (p1k1 - p1k1 - 1)·(p2k2 - p2k2 - 1)·... (pnkn - pnkn - 1). Factorization of n can be done in  time.
time.
E. Backup
In this problem we are given a rooted tree. At one step, one node is removed. If the node is being removed and its immediate ancestor is still present, the value in this ancestor is increased by 1 (initially all values are equal to 1). If the value of some node is equal to k, it should be removed at the next step. The goal is to maximize the number of step when root is removed.
Notice, that if the root has only k - 1 descendant we can remove the whole tree before touching the node n. Otherwise, descendants should be split in three sets: totally removed subtrees, subtrees with their root remaining, and one subtree, whose root is removed at the end causing the node n to be removed as well. Run depth-first search to compute the following value of dynamic programming:
a(v) is the number of nodes we can remove in subtree of v if we are allowed to remove v at any point. One can show that a(v) equals the total number of nodes in the subtree.
b(v) is the number of nodes we can remove in subtree of v if we are not allowed to touch node v. If there are less than k - 1 descendants, b(v) is equal to a(v) - 1. Otherwise, we should pick k - 2 descendant to use value a(u), while for other we use b(u). This k - 2 descendants are selected by maximum value of a(u) - b(u).
c(v) equal to the number of nodes we can remove if we are allowed to remove node v but this should be done at the very end. Value of c(n) is the final answer. We have to select some k - 2 descendants to use a(u), one to use c(u) and for others we take b(u). Try every descendant as a candidate for c(u) and for other use greedy algorithm to pick best a(u) - b(u). Precompute the sorted array of all descendants and compute the sum of k - 2 best. If descendant x to be used with c(x) is among these k - 2 use the k - 1 (there should be at least k - 1 descendants, otherwise we destroy the whole subtree).
The overall complexity is  .
.
F. Lying Processors
We are going to use the fact that n ≤ 7 and compute profile dynamic programming. If we already filled first i columns of the table and everything is correct for first i - 1 columns, we only need to know the state of last to columns in order to be able to continue.
Let dp(i, m1, m2), where i varies from 1 to m, m1 and m2 are bitmasks in range from 0 to 2n - 1 mean the minimum number of processors required to fill first i columns in order to make first i - 1 columns correct and last two columns be filled as m1 and m2 respectively. The number of different states is O(m·22n). Finally, to compute the relaxations we try all possible masks m3 for the new state dp(i + 1, m2, m3).
Applying bit operations and some precomputations we obtain O(m·23n) running time. We can speed it up a lot by precomputing all valid m3 for a pair of (m1, m2).
Exercise: come up with O(nm22n) solution.
Hello everybody!
Yandex.Algorithm 2018 team is glad to announce that the registration for the seventh competitive programming (and even more) championship held by Yandex is open! The championship is a wonderful opportunity to practice with interesting problems, compete against addicted programmers all over the world, and battle for a brand T-shirt. As usual, 25 most successful addicted competitive programmers will be invited to onsite finals that will be held in Saint Petersburg on May, 19.
In case you feel tired of classical competitive programming problems style, or just seek for competitions of any possible kind, you might be interested in new tracks we announce: optimization and ML.
Warm-up round will take place this Sunday!
UPD: link to warm-up round.
UPD2: editorial is here!

Problem A. Long-Term Mail Storage.
The probelm asked to simply simulate the process. One can keep yet unread mails in any data structure (array, deque, set, whatever) and iterate through time. For any moment of time x we first check whether there is a new incoming letter and add it to the structure if that is the case. Now, check if the ``feeling guilty'' condition is satisfied. If so, compute k and remove k oldest letter from the structure. Doing all this in the most straightforward way would result in O(nT) complexity.
Excercise: solve the problem in O(n) time.
Problem B. Lassies Versus Machine.
First of all, note that if Dusya and Lusia split n in x and n - x they would get exactly the same set of banknotes as a change as if they split in x + 5000 and n - x - 5000. That means, we only have to check all possibilities to split from a to min(a + 5000, n - a). For each possibility we compute the change in O(1) time. If some girl wants to pay y the change will be (5000k - y) mod 500, where  .
.
Excercise: prove that it's enough to check only values from a to min(a + 499, n - a).
Problem C. Effecient Management Returns.
There are many different approaches for this problem and almost all solutions one can imagine will work as the size of the answer will never exceed 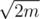 (excersise: prove). This editorial contains only one possible linear time solution.
(excersise: prove). This editorial contains only one possible linear time solution.
Proceed vertices one by one. After we have processed first i - 1 vertices (v1, v2, ..., vi - 1) we would like to keep a way to dirstibute them among ki teams T1, T2, ..., Tki that will satisfy all the requirements. When we add a new node vi we should find any component Tj, such that there is no node  and
and 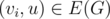 . Assuming
. Assuming 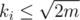 this can be done in
this can be done in  time by simply making an array of boolean marks and traversing the list of all neighbours. If there is no such Tj, we consider ki + 1 = ki + 1, i.e. we create a new set for this vertex. However, we actually do not need this
time by simply making an array of boolean marks and traversing the list of all neighbours. If there is no such Tj, we consider ki + 1 = ki + 1, i.e. we create a new set for this vertex. However, we actually do not need this 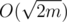 time to set up the boolean array, as we can use only one array and mark it with a number of iteration instead of a simple \emph{true}. Thus, we set marks in O(deg(vi)) time and then simply consider all sets one by one till we find first valid. Obviously, we will skip no more then deg(vi) sets till we find first possible match, thus the running time will be O(deg(vi)) and the total running time is O(n + m).
time to set up the boolean array, as we can use only one array and mark it with a number of iteration instead of a simple \emph{true}. Thus, we set marks in O(deg(vi)) time and then simply consider all sets one by one till we find first valid. Obviously, we will skip no more then deg(vi) sets till we find first possible match, thus the running time will be O(deg(vi)) and the total running time is O(n + m).
Problem D. The Sting.
First of all we would like to slightly change how we treat a bet. Define ci = ai + bi. Now, if we accept the i-th bet we immediately take bi and then pay back ci in case this bet plays. Define as A some subset of bets, 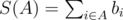 , i.e. the total profit we get from subset A. Define as L(A) the total amount we will have to pay in case the game result will be "team looses", i.e.
, i.e. the total profit we get from subset A. Define as L(A) the total amount we will have to pay in case the game result will be "team looses", i.e.  . Similarly we introduce D(A) and W(A). Now, the profit of Ostap if he accepts subset A is S(A) - max(L(A), D(A), W(A)).
. Similarly we introduce D(A) and W(A). Now, the profit of Ostap if he accepts subset A is S(A) - max(L(A), D(A), W(A)).
In this form it's not clear how to solve the problem as we simultaneously want to maximize S(A) from the one hand, but minimize maximum from the other hand. If we fix the value max(L(A), D(A), W(A)) = k the problem will be, what is the maximum possible sum of bi if we pick some subset of "loose" ("draw", "win") bets with the sum of ci not exceeding k. Such values 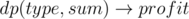 can be computed for each outcome independetly using knapsack dynamic programming. The complexity of such solution is O(nL), where
can be computed for each outcome independetly using knapsack dynamic programming. The complexity of such solution is O(nL), where  .
.
Problem E. Random Value of Mode.
To start with consider O(n2) dynamic programming solution. Let dpleft(i, j) be the optimum expected value if Gleb has visited all shops on segment from i to j inclusive and is now standing near the shop i. In the same way dpright(i, j) as the optimum expected value if segment from i to j was visited and Gleb stands near shop j.
We are not going to consider all the formulas there, but here is how we compute dpleft(i, j), picking the minimum of two possibilities go left or go right:
,
To move forward we should have a guess that if there are no pi = 0 we are going to visit many shops with a really small probability. Indeed, the smallest possible positive probability is one percent, that is 0.01 which is pretty large. The probability to visit k shops with pi > 0 and not find a proper coat is 0.99k, that for k = 5000 is about 1.5·10 - 22. Assuming ti ≤ 1000 and n ≤ 300 000 the time required to visit the whole mall is not greater than 109, thus for k = 5000 it will affect the answer by less than 10 - 12. Actually, assuming we only need relative error k = 3000 will be sufficient.
Now, we find no more than k shops with pi > 0 and i < x and no more than k shops with pi > 0 and i > x. Compress shops with pi = 0 between them and compute quaratic dynamic programming. The overall running time will be O(n + k2).
Problem F. Measure Twice, Divide Once.
We need to assign each vertex a single positive integer xv~--- the number of the process iteration when this vertex will be deleted. For the reason that will be clear soon we will consider xv = 0 to stand for the last iteration, i.e. the greater value of x correspond to the earlier iterations of the process. One can prove that an assignment of positive integers xv is correct if and only if for any two vertices u and v such that xu = xv the maximum value of xw for all w on the path in the tree from u to v is greater than xu. That is necessary and sufficient condition for any two vertices removed during one iteration to be in different components.
Pick any node as a root of the tree. Denote as C(v) the set of direct children of v and as S(v)~--- the subtree of node v. Now, after we set values of x in a subtree v we only care about different values of xu, 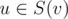 that are not "closed", i.e. there is no value greater between the corresponding node and the root of a subtree (node v). Denote as d(v, mask) boolean value whether it's possible to set values of x in a subtree of node v to have values mask unclosed. Because of centroid decomposition we know there is no need to use values of x greater than
that are not "closed", i.e. there is no value greater between the corresponding node and the root of a subtree (node v). Denote as d(v, mask) boolean value whether it's possible to set values of x in a subtree of node v to have values mask unclosed. Because of centroid decomposition we know there is no need to use values of x greater than 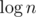 , thus there are no more than
, thus there are no more than 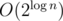 different values of mask, i.e. O(n). d(v, mask) can be recomputed if we know d(u, mask) for all
different values of mask, i.e. O(n). d(v, mask) can be recomputed if we know d(u, mask) for all 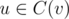 in O(n3) time. Indeed, if one child ui uses mask mi we know:-
in O(n3) time. Indeed, if one child ui uses mask mi we know:-
- We have to set xv greater than any i that occurs in more than one mask.
- We can set xv to any i that doesn't occur in any mi.
- If we set xv = i, all j < i are set to 0 in m.
Now, one can notices that according to the following process if mask m1 is a submask of m2 it is always better lexicographically smaller than mask m2 it always affects the result in a better way. Now, we claim that if for some subtree v we consider the minimum possible m, such that d(v, m) is true, for each m1 > m there exists m2 submask of m1 such that d(v, m2) is true. Indeed, consider the first (highest) bit i where m and m1 differ. Because m1 is greater than m it will have 1 at this position, while m will have 0. If there is no 1 in m anymore it is itself a submask of m1, otherwise, this means xv < i. We can set xv = i and obtain a submask of m1.
The above means we should only care about obtaining a lexicographically smallest mask for each subtree S(v). To do this we use the above rules to merge the results in all 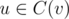 . This can be easily done in
. This can be easily done in  or in O(n) if one uses a lot of bitwise operations.
or in O(n) if one uses a lot of bitwise operations.
Hello everybody!
Tomorrow, at 10:00 Moscow time will be held Round 1 of Yandex.Algorithm competition, authored by me. I would like to thank Zlobober for all the job he does to make this competition interesting, MikeMirzayanov for the great polygon that ease the preparation process a lot, and everyone, who tested the round and made useful comments. Of course, we did our best to make the problem diverse by topics and difficulty.
See you in the competition dashboard!
UPD Thanks to everyone who participated, hope each of you found at least one interesting problem. We apologize for the situation with problem F, we have googled for all the problems and asked all testers whether they have seen such problems or not, but that didn't helped. The editorial has been published.
I've already expressed everything in this comment, however, I've decided to additionally create this post to raise the attention to what I consider to be a very serious and frustrating issue.
Hello everybody!
Tomorrow round will be held using problemset of Moscow programming competition for school students of grades from 6 to 9. Do not be tricked by the age range of the participants, Moscow jury always tries its best to select interesting problems of various topics. Problems were developed by feldsherov, ch_egor, halin.george, ipavlov and GlebsHP.
Hope to see you in the standings!
P.S. Scoring distribution is standard.
UPD Congratulations to the winners!
UPD2 Problem analysis is here.
Dear community!
It was a fantastic year, with great pleasure I took a role of Codeforces Coordinator. This year I learned a lot, communicated with wonderful people and realized how valuable this work is for thousands of people. I would like to thank you all for these great moments! I strongly believe that there are many cool rounds and interesting problems ahead as I'm passing this duty to Nikolay KAN Kalinin!
Please, watch my New Year's speech (Russian language, English subtitles):
P.S. Special thanks go to Maxim Zlobober Akhmedov and Oleg mingaleg Mingalev who helped me prepare this video.
Finally, the analysis is here! Feel free to ask in comments for any unclear part.
Problems ideas and development:
Cards: MikeMirzayanov, fcspartakm
Cells Not Under Attack: GlebsHP, fcspartakm
They Are Everywhere: MikeMirzayanov, fcspartakm
As Fast As Possible: GlebsHP, fcspartakm
Connecting Universities: GlebsHP, fcspartakm, danilka.pro
Break Up: GlebsHP, MikeMirzayanov, kuviman
Huffman Coding on Segment: GlebsHP, Endagorion
Cool Slogans: GlebsHP
Hello everybody!
Today the second regular rated round based on problems of VK Cup 2016 Final Round will take place. Of course, we have created some more easy problems to fulfill the requirements of different skill levels and make the contest interesting for everyone.
The commentators of the previous announcement pointed out that I forgot to thank MikeMirzayanov for making Codeforces and Polygon so awesome. I was wrong, Mike, that's really cool :)
Scoring distribution will be published right before the start of the contest. We wish you good luck and beautiful solutions!
UPD1. Scoring for div2: 500-750-1000-1500-2000-2500. Scoring for div1: 500-1000-1500-2250-3000.
UPD2. The contest is over, congratulations to winners!
Div1:
Div2:
UPD3. I sincerely apologize for the delay with problem analysis. I was out of town for a vacation. Here it is.
New problems will be added as soon as the analysis is ready.
Dear friends!
We are glad to invite you to take part in Codeforces Round #363, featuring some problems of the VK Cup 2016 Final Round that took place in Saint Petersburg at the beginning of July. The second part of the problemset will be used to conduct Codeforces Round #364. Of course, we made some new problems to complete the set to fulfill the requirements of the regular round and it now contains problems of the appropriate difficulty for participants of any color.
We will obey the good old tradition to publish the scoring distribution right before the start of the competition.
We wish you good luck and an interesting contest!
UPD1. Scoring distribution will be standard in both divisions 500-1000-1500-2000-2500-3000 (yes, there will be six problems featured in both div1 and div2).
UPD2. Problems were prepared for you by MikeMirzayanov, Errichto, fcspartakm, qwerty787788 and Radewoosh.
UPD3. System testing is over, congratulations to winners!
Div. 1:
Div. 2:
UPD4. Analysis is almost here
Hello, community!
Tomorrow Codeforces Round #342 is going to take place. It will share the problemset with Moscow Olympiads in Informatics for students of grades from 6 to 9. Though, grades from 6 to 9 in Russia usually match the ages from 12 to 15, I guarantee that everyone (even Div. 1 participants) will find some interesting problems to solve. Problems were selected for you by the Moscow jury team: Zlobober, meshanya, romanandreev, Helena Andreeva and me; and prepared by members of our scientific committee: wilwell, Sender, iskhakovt, thefacetakt and feldsherov.
Scoring distribution will be quite unusual: 750-750-1000-2000-3000.
UPD System testing is over. Here are the top 10:
Congratulation! Also, problems seemed to be too tough, we should have probably made Div. 1 round. Anyway, thanks for participating, I hope you enjoyed it and learned something new!
Thanks to romanandreev for nice analysis.
I like the idea of Endagorion to supplement the problems analysis with small challenges, somehow related to the problem preparation, it's generalization, or more effective solution. Following this, some problems in this analysis are also complemented with this sort of tasks.
Div. 2A (Wizards' Duel)
Idea of the problem: Roman Gusarev, development: timgaripov.
Let's start with determining the position of the first collision. Two impulses converge with a speed p + q, so the first collision will occur after 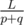 seconds. The coordinate of this collision is given by the formula
seconds. The coordinate of this collision is given by the formula 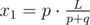 .
.
Note, that the distance one impulse passes while returning to it's caster is equal to the distance it has passed from the caster to the first collision. That means impulses will reach their casters simultaneously, and the situation will be identic to the beginning of the duel. Hence, the second collision (third, fourth, etc) will occur at exactly the same place as the first one.
Code example: 13836780.
Div. 2B (Rebranding)
Idea of the problem: glebushka98, development: thefacetakt.
Trivial solution will just emulate the work of all designers, every time considering all characters of the string one by one and replacing all xi with yi and vice versa. This will work in O(n·m) and get TL.
First one should note that same characters always end as a same characters, meaning the position of the letter doesn't affect the result in any way. One should only remember the mapping for all distinct characters. Let p(i, c) be the mapping of c after i designers already finished their job. Now:
- p(0, c) = c
- If p(i - 1, c) = xi, then p(i, c) = yi
- Same, if p(i - 1, c) = yi, then p(i, c) = xi
This solution complexity is O(|Σ|·m + n) and is enough to pass all the tests.
Challenge: improve the complexity to O(Σ + n + m).
Code examples: 13837577 implements O(|Σ|·m + n) and 13839154 stands for O(|Σ| + n + m).
Div. 2C\Div. 1A (Median Smoothing)
Problem idea and development: Sender.
We will call the element of a sequence stable, if it doesn't change after applying the algorithm of median smoothing for any number of times. Both ends are stable by the definition of the median smoothing. Also, it is easy to notice, that two equal consecutive elements are both stable.
Now we should take a look at how do stable elements affect their neighbors. Suppose ai - 1 = ai, meaning i - 1 and i are stable. Additionaly assume, that ai + 1 is not a stable element, hence ai + 1 ≠ ai and ai + 1 ≠ ai + 2. Keeping in mind that only 0 and 1 values are possible, we conclude that ai = ai + 2 and applying a median smoothing algorithm to this sequence will result in ai = ai + 1. That means, if there is a stable element in position i, both i + 1 and i - 1 are guaranteed to be stable after one application of median smoothing. Now we can conclude, that all sequences will turn to stable at some point.
Note, that if there are two stable elements i and j with no other stable elements located between them, the sequence of elements between them is alternating, i.e. ak = (ai + k - i)mod2, where 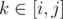 . One can check, that stable elements may occur only at the ends of the alternating sequence, meaning the sequence will remain alternating until it will be killed by effect spreading from ending stable elements.
. One can check, that stable elements may occur only at the ends of the alternating sequence, meaning the sequence will remain alternating until it will be killed by effect spreading from ending stable elements.
The solution is: calculate max(min(|i - sj|)), where sj are the initial stable elements. Time complexity is O(n).
Challenge 1: hack the solution that just applies median smoothing until something changes.
Challenge 2: think of how to speed up the algorithm from challenge 1 using bitmasks (still gets TL).
Code examples: 13838940 and 13838480.
Div. 2D\Div. 1B (Chip 'n Dale Rescue Rangers)
Problem idea and development: StopKran.
If the velocity of the dirigible relative to the air is given by the vector (ax, ay), while the velocity of the wind is (bx, by), the resulting velocity of the dirigible relative to the plane is (ax + bx, ay + by).
The main idea here is that the answer function is monotonous. If the dirigible is able to reach to target in  seconds, then it can do so in
seconds, then it can do so in  seconds, for any x ≥ 0. That is an obvious consequence from the fact the maximum self speed of the dirigible is strictly greater then the speed of the wind at any moment of time.
seconds, for any x ≥ 0. That is an obvious consequence from the fact the maximum self speed of the dirigible is strictly greater then the speed of the wind at any moment of time.
For any monotonous function we can use binary search. Now we only need to check, if for some given value  it's possible for the dirigible to reach the target in
it's possible for the dirigible to reach the target in  seconds. Let's separate the movement of the air and the movement of the dirigible in the air. The movement cause by the air is:
seconds. Let's separate the movement of the air and the movement of the dirigible in the air. The movement cause by the air is:
- (xn, yn) =
 , if
, if 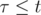 ;
; - (xn, yn) =
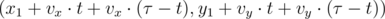 , for
, for 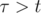 .
.
The only thing we need to check now is that the distance between the point (xn, yn) and the target coordinates (x2, y2) can be covered moving with the speed vmax in  seconds assuming there is no wind.
seconds assuming there is no wind.
Time complexity is 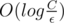 , where C stands for the maximum coordinate, аnd ε — desired accuracy.
, where C stands for the maximum coordinate, аnd ε — desired accuracy.
Challenge 1: think of the solution in case it's not guaranteed that the dirigible is faster than the wind.
Challenge 2: can you come up with O(1) solution?
Code examples: 13838659 and 13842505.
Div. 2E\Div. 1C (Three States)
Problem idea and development: haku.
Affirmation. Suppose we are given an undirected unweighted connected graph and three distinct chosen vertices u, v, w of this graph. We state that at least one minimum connecting network for these three vertices has the following form: some vertex c is chosen and the resulting network is obtained as a union of shortest paths from c to each of the chosen vertices.
Proof. One of the optimal subgraphs connecting these three vertices is always a tree. Really, we can take any connecting subgraph and while there are cycles remaining in it, take any cycle and throw away any edge of this cycle. Moreover, only vertices u, v and w are allowed to be leaves of this tree, as we can delete from the network any other leaves and the network will still be connected. If the tree has no more than three leaves, it has no more than one vertex with the degree greater than 2. This vertex is c from the statement above. Any path from c to the leaves may obviously be replaced with the shortest path. Special case is than there is no node with the degree greater than 2, meaning one of u, v or w lies on the shortest path connecting two other vertices.
The solution is: find the shortest path from each of the chosen vertices to all other vertices, and then try every vertex of the graph as c. Time complexity is O(|V| + |E|).
To apply this solution to the given problem we should first build a graph, where cells of the table stand for the vertices and two vertices are connected by an edge, if the corresponding cells were neighboring. Now we should merge all vertices of a single state in one in order to obtain a task described in the beginning. Time complexity is a linear function of the size of the table 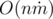 .
.
Code examples: 13843265 — the solution described above that uses 0-1 bfs instead of merging, 13840329 — another approach that tries to different cases.
Div. 1D (Top Secret Task)
Problem idea and development: glebushka98.
If 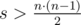 , than the sum of k minimums is obviously an answer.
, than the sum of k minimums is obviously an answer.
Let i1 < i2 < ... < ik be the indices of the elements that will form the answer. Note, that the relative order of the chosen subset will remain the same, as there is no reason to swap two elements that will both be included in the answer. The minimum number of operations required to place this k elements at the beginning is equal to 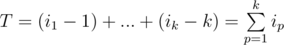 —
— 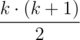 .
.
T ≤ S 
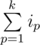 ≤
≤ 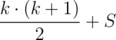 .
. 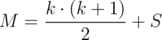 .
.
Calculate the dynamic programming d[i][j][p] &mdash minimum possible sum, if we chose j elements among first i with the total indices sum no greater than p. In order to optimize the memory consumption we will keep in memory only two latest layers of the dp.
Time complexity is O(n4), with O(n3) memory consumption.
Code examples: 13845513 and 13845571.
Div. 1E (Birthday)
Problem idea: meshanya, development: romanandreev.
The given problem actually consists of two separate problems: build the directed graph of substring relation and find the maximum independent set in it. Note, that if the string s2 is a substring of some string s1, while string s3 is a substring of the string s2, then s3 is a substring of s1. That means the graph of substring relation defines a partially ordered set.
To build the graph one can use Aho-Corasick algorithm. Usage of this structure allow to build all essential arc of the graph in time O(L), where L stands for the total length of all strings in the input. We will call the arc  essential, if there is no w, such that
essential, if there is no w, such that  and
and  . One of the ways to do so is:
. One of the ways to do so is:
- Build Aho-Corasick using all strings in the input;
- For every node of the Aho-Corasick structure find and remember the nearest terminal node in the suffix-link path;
- Once again traverse all strings through Aho-Corasick. Every time new symbol is added, add an arc from the node corresponding to the current string (in the graph we build, not Aho-Corasick) to the node of the graph corresponding to the nearest terminal in the suffix-link path;
- The previous step will build all essential arcs plus some other arcs, but they do not affect the next step in any way;
- Find the transitive closure of the graph.
To solve the second part of the problem one should use the Dilworth theorem. The way to restore the answer subset comes from the constructive proof of the theorem.
Time complexity is
Unable to parse markup [type=CF_TEX]
to build the graph plus O(n3) to find the maximum antichain. The overall complexity is O(L + n3).Congratulation to ikatanic — — the only participant to solve this problem during the contest. View his code 13851141 for further clarifications.
Challenge: solve the problem with the same asymptotic, if we are to find the subset with the maximum total length of all strings in it.
Hello, dear participants of Codeforces community!
Starting from Codeforces Round #327 I'll be the new coordinator and will manage preparation process for all regular Codeforces rounds and other contests held on this platform. I'll do my best to increase the quality of contests we offer you, though Zlobober already raised this bar high. Let's cheer him once again, for all the great job he had done!
Tomorrow round will be held using the problems of Moscow team olympiad for high-school students. Do not be tricked by the word "school" — there will be a gold medalist of IOI 2015 participating and some candidates to this year Russian IOI team, meaning the level of the problems will be appropriate. I am sure everyone will find an interesting problem to enjoy.
The problemset was prepared by the team of Moscow authors (list is incomplete): Zlobober, romanandreev, meshanya, wilwell, glebushka98, timgaripov, thefacetakt, haku, LHiC, Timus, Sender, sankear, iskhakovt, andrewgark, ipavlov, StopKran, AleX leaded by your humble servant GlebsHP and the chairman of the jury Helen Andreeva.
Special thanks to Delinur for translation and stella_marine for correction.
Five problems will be offered in both divisions and the scoring distribution will be announced later (good traditions should live).
UPD. Round time. Please note that Russia is not changing the timezone this night, while about 100 countries do so. Be sure to check when round starts in your timezone!
UPD2. Please note, that the distribution motivates you to read all the problems! Div1.: 750-1000-1250-1750-2500 Div2.: 500-1000-1750-2000-2250
UPD3. The results and the editorial will be published later, after the closing ceremony of the official competition.
UPD4. The system testing is over, results are now final. Feel free to upsolve and read other contestants code. Congratulations to Div. 1 top-5:
UPD5. Problem analysis is now available.
| Name |
|---|










