Problem 1466I - The Riddle of the Sphinx, authored by gawry and Anadi, raised some interesting questions. The problem asks to find the maximum among $$$n$$$ secret $$$b$$$-bit $$$a_1 \ldots a_n$$$ numbers using $$$3n+3b$$$ questions of the form "is $$$a_i$$$ at most $$$x$$$"? ecnerwala described a solution using only $$$2n+2b-2$$$ questions. Here I will describe a solution using only $$$2n + 1.45b$$$ questions, using Fibonacci numbers instead of powers of two. In a sense this solution looks near-optimal, but there are better solutions when one of $$$n, b$$$ is much smaller than the other. In the other direction, a fairly simple argument shows that $$$n + b - 1$$$ questions are always needed in the worst case. I'll also sketch a proof that $$$n + b + 0.3 \min(n, b)$$$ (maybe minus some constant term) questions are needed. This shows that no solution can hope to achieve e.g $$$1.1 n + 1.1 b$$$, but still leaves a wide gap to $$$2n + 1.45b$$$.
I'll be sloppy with $$$+O(1)$$$ terms throughout, so while we are interested in the difference between $$$n$$$ and $$$2n$$$, I might forget about the difference between $$$n$$$ and $$$n + 10$$$. The ideas here arose in discussion with noncomlp. If you any ideas on how to improve the bounds in this post, please share them!
Terminology
Throughout this post, I will be using a straightforward reformulation of the original problem. In this reformulation, the state of the game is described by a multiset $$$P$$$ of integers all at least $$$2$$$. The game ends when $$$P$$$ is empty. In one move, we may name an integer $$$r$$$. Then one of two things happen: either (one occurrence of) $$$\max P$$$ is replaced by $$$r$$$, or $$$P$$$ is replaced by $$$P - r := [ p - r \mid p \in P, p - r \ge 2]$$$. The connection with the original problem comes from the observation that instead of remembering upper / lower bounds $$$u_i$$$ / $$$l_i$$$ on $$$a_i$$$ for each $$$1 \le i \le n$$$, it suffices to remember upper bounds $$$u_i$$$ and the greatest lower bound $$$L$$$ we've seen so far. We then consider the multiset $$$[ u_i - L + 1 \mid u_i > L]$$$, and observe that asking if $$$a_i \stackrel{?} \le x$$$ is like naming $$$r = x - L + 1$$$ in the reformulation. (This relies on the observation that we can always pick the $$$i$$$ which maximises $$$u_i$$$.) Thus the number of questions needed for $$$n, b$$$ is the number of moves needed to win the game starting from the multiset of size $$$n$$$ containing just the number $$$2^b$$$.
Fibonacci strategy
The problem hints to use powers of two, but let's instead use Fibonacci numbers. Basically this is motivated by the observation that if $$$\min P = F_i$$$ and we name $$$F_{i-1}$$$, then if we end up subtracting $$$F_{i-1}$$$, $$$F_i$$$ becomes $$$F_{i-2}$$$. Instead of starting from $$$P = [2^b, \ldots, 2^b]$$$, let's suppose we start from $$$P = [F_c, \ldots, F_{c+n-1}]$$$. I'll describe a solution which uses only $$$2n + c$$$ questions. This solves the original problem in $$$2n + 1.45b$$$ questions, where $$$1.45 = \log_2 \phi$$$, since $$$F_{n+1} \ge \phi^n$$$.
It is necessary to consider a more general class of multisets than the one above, since we might end subtracting Fibonacci numbers from much larger Fibonacci numbers. We'll assume we have some $$$c \ge 3$$$ and a string $$$S$$$ containing characters 1 and x, where no x is followed by another x. The multiset $$$P = P(c, S)$$$ is then read off as $$$P(c, \emptyset) = \emptyset$$$, $$$P(c, 1S) = [F_c] \cup P(c+1, S)$$$, $$$P(c, xS) = P(c+1, S) - F_c$$$. Thus the multiset above corresponds to the string $$$S$$$ of $$$n$$$ 1s. We claim that any such state can be done in $$$2n + c$$$ questions, where $$$n$$$ is the number of 1s in $$$S$$$.
The strategy in this class is fairly simple. We always name $$$F_{c-1}$$$. In the case where $$$\max P$$$ is replaced by $$$F_{c-1}$$$, we simply move the last 1 of $$$S$$$ to the start, and subtract one from $$$c$$$. In the case where $$$F_{c-1}$$$ is subtracted from all elements of $$$P$$$, we prepend an x to $$$S$$$ and subtract one from $$$c$$$. Now if the string looks like xx1T, then we reduce it to xT, and increase c by 2. This doesn't change $$$P(c, S)$$$ (since $$$F_c + F_{c+1} = F_{c+2}$$$), nor our monovariant $$$2n + c$$$, and after repeatedly doing this operation, no x in $$$S$$$ is followed by another x.
We should be careful to note that $$$c$$$ need never be negative, since we don't want negative Fibonacci numbers, and we also don't want our monovariant to go negative. Indeed already if $$$c = 2$$$, we can increase $$$c$$$ and remove the first one or two characters of $$$S$$$, since they give some number which is at most $$$1$$$.
Here is my implementation of this strategy: 103038134.
Lower bounds
Here is a nice fact: if some strategy never finishes in less than $$$z$$$ moves starting from $$$P$$$, then no strategy can guarantee to finish in less than $$$z$$$ moves starting from $$$P$$$. The proof is simple. Say, starting from $$$P$$$, the first strategy names $$$r$$$, and the second strategy names $$$t$$$. If $$$r \le t$$$, consider what happens when $$$\max$$$ is replaced by $$$r$$$ or $$$t$$$: the first strategy is better off. On the other hand, if $$$r \ge t$$$, then when $$$r$$$ or $$$t$$$ is subtracted from all numbers, then the first strategy is better off.
Thus the problem of showing that no strategy always does well reduces to finding a strategy which never does well. Here is one such strategy, starting from $$$P = [2^b, \ldots, 2^b]$$$ (size $$$n$$$). If $$$b = 1$$$, then we name $$$r = 0$$$. If $$$b \ge 1$$$, then we name $$$2^{b-1}$$$. In the best case, $$$b$$$ decreases by $$$1$$$ each step until $$$b = 1$$$, at which point $$$n$$$ decreases by $$$1$$$ each step until $$$n = 0$$$. Thus $$$n + b - 1$$$ questions are needed.
The Fibonacci strategy looks like a good candidate for "strategy that never does well", since the monovariant should decrease by exactly 1 in every step. Unfortunately, it can start doing well in special cases, like when $$$c$$$ or $$$n$$$ is too small. There is a good reason for this, explained in the next section. For the rest of this section, I'll sketch a modified Fibonacci strategy which really never does too well.
Where we previously considered the alphabet with two letters 1 and x, let's now expand the alphabet to allow for arbitrary non-negative integers. Where (c, "1") corresponds to $$$[F_c]$$$, we'll let (c,"m") correspond to $$$[F_c, \ldots, F_c]$$$ (size $$$m$$$). The states we consider are given by $$$c\ge 3$$$ and strings $$$S$$$ of the form above followed by a string 0m with $$$m \ge 1$$$. Thus our initial state looks like (c, 0n). Our strategy is the same as before (instead of moving 1s from end to beginning, we replace n with (n-1) and put a 1 at the beginning), with the added reduction rule (c, x0m) -> (c, 0m) (corresponding to $$$F_{c+2} - F_c = F_{c+1}$$$). Eventually $$$c$$$ or $$$m$$$ gets small enough that we can't stay in this class of states, and our strategy might start doing well. But for the first $$$M := \min(c, n) - 5$$$ moves, we'll certainly stay in this class. Thus for the first $$$M$$$ turns, the monovariant decreases by at most 1. After these first $$$M$$$ turns, we consider the lower bound $$$|P| + \log_2 \min P$$$ from before. The most this could decrease after $$$M$$$ turns is $$$M \log_2 \phi$$$.
Taken together, this means that in the original problem with $$$n, b$$$, $$$n > M + 5$$$, $$$2^b > F_{M+5}$$$, at least $$$M + n + b - M \log_2 \phi > n + b + 0.3M$$$ questions are needed.
Good strategies when either $$$n$$$ or $$$b$$$ is small
A silly strategy is to always name $$$1$$$. This always wins in at most $$$|P| + \max P - 2$$$ moves. So we get a lower bound on the original problem of $$$n + 2^b - 2$$$. Note that this is better than $$$2n$$$ when $$$b$$$ is very small.
At the other extreme, consider $$$n$$$ fixed. I claim that the answer is $$$(1 + o(1)) b$$$ as $$$b \to \infty$$$. The idea is to pick some positive integer parameter $$$D$$$, and consider multisets of the form $$$[2^k | k \in Q]$$$, where $$$\max Q - \min Q \le D$$$. Given such a state, I claim that we can finish in $$$\min Q + (D+1)|Q| + \sum Q / D$$$ moves. Indeed if $$$\max Q - \min Q < D$$$, then we can name $$$2^{\min Q-1}$$$, and $$$\min Q$$$ decreases by 1. If $$$\max Q = \min Q + D$$$, then we name $$$2^{\min Q}$$$. Now either $$$|Q|$$$ decreases by $$$1$$$ and $$$\min Q$$$ increases by at most $$$D$$$, or $$$\sum Q$$$ decreases by $$$1$$$.
In the original problem, we start with $$$\min Q = \max Q = b$$$, $$$|Q| = n$$$, $$$\sum Q = bn$$$. The optimal value of $$$D$$$ is about $$$\sqrt b$$$. This shows that we need at most about $$$2 n\sqrt b + b$$$ questions. This is good when $$$n \ll \sqrt b$$$.








 and
and 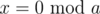 , and then return
, and then return 

