Hi! Modular inverses are used in the solutions to a lot of number theory problems, such as 622F - The Sum of the k-th Powers from the latest educational round. I want to share a one-liner (essentially) that computes modular inverse with the same complexity as the exteneded Euclidean algorithm (a and b are supposed to be positive co-prime integers, and inv(a,b) is the inverse of a modulo b, lying between 1 and b):
long long inv(long long a, long long b){
return 1<a ? b - inv(b%a,a)*b/a : 1;
}
The idea behind the code is that to compute inv(a,b), we find x such that  and
and 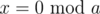 , and then return
, and then return x/a. To find x, we can write x = yb + 1 and solve for y by recursively computing inv(b,a). (Actually inv(b%a,a))
This isn't the fastest method if you're worried about performance, and you will probably get overflow if a*b doesn't fit inside a long long. But I think it's neat.






