I was working on an interesting problem. (Tip: Homework of algorithm courses can be fun!)
Find the minimum number of (directed) edges to introduce into a directed graph to make it strongly connected (from any vertex you can go to any other vertex). Also, find one configuration of edges to add that satisfies the property and reaches the minimum.
I wonder if this problem is a well-known problem, and if any, what name it is known with? I saw this Stack Overflow question which asks about the minimum number of edges only, not finding one such configuration, and it's said to be "a really classical problem".
I also wonder if there is a more efficient algorithm. My algorithm works in O(V3), which involves several steps to reduce the graph in question into a directed acyclic graph, a weakly connected directed acyclic graph, a connected bipartite graph, and finally giving the answer. A friend says that there is a literature on the internet giving 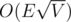 algorithm, but I haven't managed to find it. Or is there an even better algorithm?
algorithm, but I haven't managed to find it. Or is there an even better algorithm?










