rembocoder's blog

The sum of the k-th powers of the first n positive integers – easy algorithm
By rembocoder, history, 14 months ago, translation, In English

Suppose you want to know this sum for some n and k:

Here are the well known formulas for the first several k:

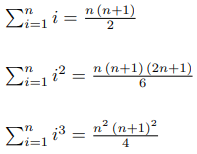
But suppose you forgot them. What to do? Luckily, there is an easy algorithm to generate those formulas.

First of all, let's prove a theorem.

Theorem

Suppose for every integer non-negative n:

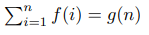
where f and g are polynoms. Then for some constant c:

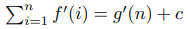
Proof

For every positive integer n:

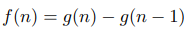
These two polynoms are equal in an infinite number of points, which means that they are identical. Which allows us to say:

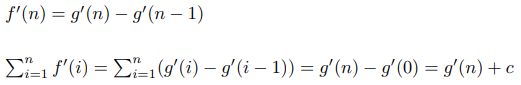
Application

Let's say we want to find the formula for the sum of squares. Then using our theorem we can create such an algorithm:

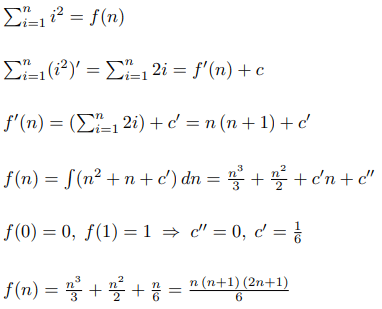
Now let's run the same algorithm to find the formula for the sum of cubes:

  • Vote: I like it
  • +87
  • Vote: I do not like it

»
14 months ago, # |
  Vote: I like it 0 Vote: I do not like it

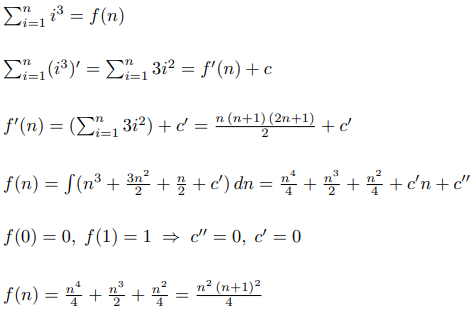
I hope the technique has already discussed in the very beginning chapter of Knuth's Concrete Math book.

→ Reply
»
14 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hard version: 1677F - Tokitsukaze and Gems

→ Reply
»
14 months ago, # |
← Rev. 2   Vote: I like it +13 Vote: I do not like it

Maybe the easier and more direct way (if you want to do it for all $$$k$$$ up to some limit) would be to notice that

$$$ g_k(n) - g_{k}(n-1) = \sum\limits_{i=1}^n [i^k - (i-1)^k] = \sum\limits_{i=1}^n \sum\limits_{j=1}^{k} \binom{k}{j} (-1)^{j+1} i^{k-j} $$$

But on the other hand, it's also $$$g_k(n) - g_k(n-1) = n^k$$$, hence we get the recurrence

$$$ k g_{k-1}(n) = n^k + \sum\limits_{j=2}^k \binom{k}{j} (-1)^j g_{k-j}(n), $$$

or, for $$$g_k(n)$$$, it would be

$$$ g_k(n) = \frac{1}{k+1} \left[n^{k+1} + \sum\limits_{j=1}^{k} \binom{k+1}{j+1} (-1)^{j+1} g_{k-j}(n)\right] $$$

starting with $$$g_0(n) = n$$$.

Thus,

$$$\begin{gather} g_1(n) &=& \frac{1}{2} \left[n^2 + \binom{2}{2} g_0(n)\right] &=& \frac{n(n+1)}{2}, \\ g_2(n) &=& \frac{1}{3} \left[n^3 + \binom{3}{2} g_1(n) - \binom{3}{3} g_0(n)\right] &=& \frac{n(n+1)(2n+1)}{6}, \\ g_3(n) &=& \frac{1}{4} \left[n^4 + \binom{4}{2} g_2(n) - \binom{4}{3} g_1(n) + \binom{4}{4} g_0(n)\right] &=& \frac{n^2 (n+1)^2}{4}. \end{gather}$$$
→ Reply
»
14 months ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

Also I think it would be nice to write down the algorithm from the blog in generic form for arbitrary $$$k$$$:

$$$\begin{gather} g_k(n) = \sum\limits_{t=1}^n t^k \\ g_k'(n) = c + \sum\limits_{t=1}^n k t^{k-1} = c + k g_{k-1}(n) \end{gather}$$$

From this, one gets

$$$ g_k(n) = cn + k \int g_{k-1}(n) dn, $$$

where $$$c$$$ is picked in a way that guarantees that $$$g_k(1) = 1$$$, that is

$$$ c = 1 - k \int g_{k-1}(n) dn \bigg|_{n=1}, $$$

and the free constant $$$c'$$$ that would appear from integration should be $$$c'=0$$$, as $$$g_k(0)=0$$$.

Compared to the scheme I described above, it's probably beneficial for larger $$$k$$$, as it allows to find it in $$$O(k)$$$ per term, rather than $$$O(k^2)$$$. I wonder if there is a more explicit formula for $$$c$$$...

→ Reply