If you're not familiar with cartesian trees on arrays I recommend to read this blog. Assume the graph is simple and connected and every node $$$v$$$ has a value $$$a_v$$$.The way we construct a cartesian tree on a graph is kinda similar to the construction of a centroid tree, here's how it works: Find any node with maximum value let's call it $$$u$$$, it'll be the root of the tree. Removing $$$u$$$ and its edges leaves us with several (possibly only 0) connected components, for each of those components, construct a cartesian tree and add edges from $$$u$$$ to the roots of the cartesian trees. Here's an example: 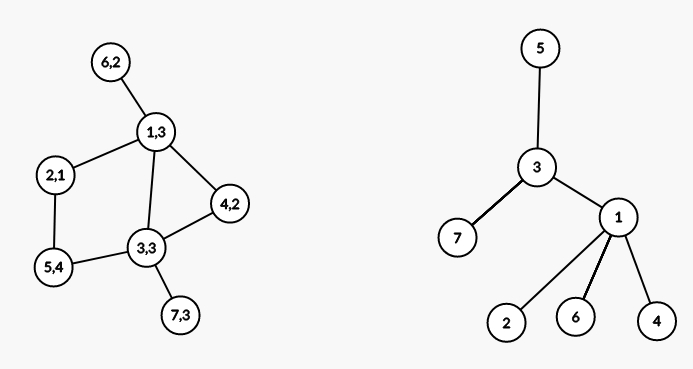
On the left, the graph, where vertices are labeled $$$v,a_v$$$ and on the right, one of the corresponding cartesian trees where vertices are labeled by their index.
How to optimize the construction:
If you naively apply the algorithm described above, you will end up with a complexity of $$$O(n^2)$$$ since unlike the centroid tree, the cartesian tree (which I will refer to as CT from now on) can be very deep. Thankfully we can construct it in $$$O(n\log(n))$$$ using the following algorithm: First, sort the nodes by their value. Next iterate over the nodes by non-decreasing order of value. Let $$$u$$$ be the current node, mark $$$u$$$ then for all neighbors $$$v$$$ of $$$u$$$, if $$$v$$$ is marked and $$$u$$$ and $$$v$$$ are not connected (which we will check using DSU), then the edge $$$u,c_v$$$ is added to the CT (where $$$c_v$$$ is the node with maximum value that is connected to $$$v$$$, this will be kept track of using DSU) and then with DSU, connect $$$u$$$ and $$$v$$$. Note that if the graph isn't connected, this algorithm will produce a forest of CTs. The proof of correctness of this algorithm is left as en exercise to the reader (I am definitely not too lazy to write the proof). You can find an implementation here
Properties:
- The CT is like a heap, since all the children of a node have a lower (possibly equal) value.
- Just like the dfs tree, all edges in the original graph connect a node to one of its ancestors or descendants in the CT
- Let the cost of a path in the original graph be the maximum value of the nodes it visits, then for any 2 nodes, the minimum cost of any path between them is the value of their LCA in the CT
- If the original graph is a tree, then the CT has most of the properties of the centroid tree other than the bound on its depth
- If the original graph is a chain, then the CT will be the same as a CT on a regular array.
There might be more interesting properties that I can't think of, if you find any please share them in the comments.Lastly, I know of only one problem which can be solved using this technique, CodeTon round 4 E, for which I came up with this idea during the contest. If you know of another problem where this idea can be used, once again please share it. This is my first tutorial so any feedback is appreciated. Thanks for reading!











I forgot to add that this algorithm is optimal, since it can be used to sort $$$n$$$ values. For that, represent every element by a node with the corresponding value and connect all these nodes to an artificial node whose value is negative infinity. the CT will be a chain whose nodes are sorted in decreasing order from the root. Since sorting has an optimal worst case complexity of $$$O(n\log(n))$$$ then the algorithm described above is optimal.