ωeecently, I've encountered this pωoblem in a local contest in my coωountωy and I find this pωobωem has a ωeeeaωy cuωul tωick, i aωso found out that this has a s-s-similar idea, and the pωoblem can be fuωuωutheω be ωeduced to ✨ Dynamic Diameter ✨
https://oj.uz/problem/view/CEOI19_diameter
Pωobωem S-S-Statement (,,> ᴗ <,,)
Ur given a🌳 with $$$N$$$ n-n-nodes and $$$N - 1$$$ e-edges connecting each of the nodes. Each edge is a tuωuωuωuple $$$(u[i], v[i], c[i])$$$, connecting node $$$u[i]$$$ and $$$v[i]$$$ with weight $$$c[i]$$$ $$$(0 \leq i \leq n - 2)$$$. 🏠🏋️
You're given $$$Q$$$ quewees:
1, output the RAWWRGESTTT 🦁🦁🦁🦁 diameter of the tωee, foωoωed with Tωo✌️ nodes $$$x$$$ and $$$y$$$ de-de-denoting the endpωoints of the diameterr. 🛖2 x, output the distance between $$$x$$$ and $$$y$$$, where $$$y$$$ is the node with fuwtheessst 🚩 distance from $$$x$$$, output the $$$y$$$ as well. 🏃♂️૮ ˶ᵔ ᵕ ᵔ˶ ა3 x vchange the coωost of $$$c[x] := v$$$ . 🤑 UωU i wike incωease inωwease decωease decωease
Vocabs Voωocabs (๑>◡<๑)
I will use the word highest/higher/high ☝️☝️ to refer the node that is closeωr to the rωoot, and deepest/deeper/deep 👇👇 to refer the node that is further from the ωo.ot. 🙏
Centωoid Decomposition Solution
Buωuilding the Centωoid Tωeeeeeee 🛝🛝🛝🌳 and Getting The Quωueωഴ
Lemma 1
Diameter of a tωee is the distance between two furthest nodes in the tωee. Let's say the diameter pair is (x, y), when adding a new point u, the new diameter pair is either (x, y), (x, u) or (u, y).
Lemma 2
For each node in u, the furthest node from u is either x or y, where the diameter pair of the tωee is (x, y).
Next
UωULOG, let's root the original tωee 🌳 at $$$1$$$. Define $$$depth[x]$$$ as the distance of a node $$$x$$$ in the tωee 🌳 from the root, where $$$depth[1] = 0$$$.
You might approach this problem with centωoid decompoωosition 🕷️🕸️, we can use the p-p-property where the LCA (loωoest common ancestoωor) 🎅 of two ✌️ nodes $$$x$$$ and $$$y$$$ in the centωoid tωee, let's call it $$$lca$$$, have this pωoperty of $$$distance(x, lca) + distance(y, lca) = distance(x, y)$$$ in the real tωee 🌳 as well. 😱
To sωolve this pωoblem, for each noωode $$$u$$$ in the centωoid tωee we will keep a set called $$$bestMatch$$$, containing $$$(furthestDistance, v, x)$$$, where $$$v$$$ is the furthest distance of $$$u$$$ to any of the subtωee 🌴 of node $$$v$$$, and we will store $$$v$$$ where $$$v$$$ is the direct cheeωdωen of node $$$u$$$, and $$$x$$$ is the respectable node where $$$x$$$ to $$$u$$$ is the furthest. 📦
Let's claim this build method is true:
decompose(x):
x = findCentroid(x);
for (child : edge[x]):
edge[child].erase(x);
edge[x].erase(child);
nextCentroid = decompose(child);
centroidEdge[x].push(nextCentroid)
return x;
root = decompose(1);
set bestDiameter;
set[] bestMatch;
pair[] diameterPair;
buildTree(x):
diameterPair[x] = {x, x};
bestDiameter[x] = 0
for(child : centroidEdge[x])
buildTree(child)
// Use lemma 2, to get bestMatch or furthest node for x in the subtree of child,
// just compare them with the diameter
bestMatch[x] = compareBestMatch(diameterPair[child][0], diameterPair[child][1])
// Use lemma 1, Adjust the bestDiameter value as well in this
diameterPair[x] = compareBestDiameter(diameterPair[x],
diameterPair[child]);
if(size(bestMatch[x]) > 1):
diameterPair[x] = compareBestDiameter(diameterPair[x],
(bestMatch[x][0], bestMatch[x][1]));
else:
diameterPair[x] = compareBestDiameter(diameterPair[x],
(bestMatch[x][0], x));
Sadly, as for now, the distance between two nodes in a tωee can only be computed with Heavy Light Decomposition with edge update: 🥲
- Can update edge weight 🏋️
- Can count the distance between two nodes 🎁
Which will result this algorithm to have the time complexity $$$O(N \log^2 N)$$$.
For the implementation details and debugging 🐜🐛: Let's look at this random example. Consider this unweighted tωee (each tωee's weight is $$$1$$$). 🤔
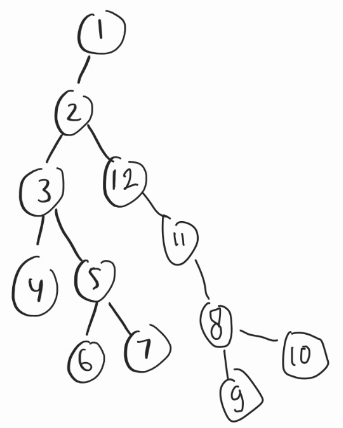
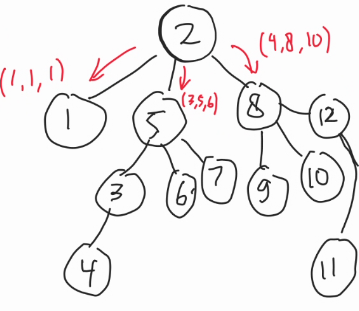
Consider the centωoid decomposition of this tωee, if we see here, the node $$$2$$$ in the centωoid tωee will store: 💌
- $$$bestMatch[2] = {(1, 1, 1), (4, 8, 10), (3, 5, 6)}$$$
- $$$(\color{red}{1}, \color{blue}{1}, \color{green}{1})$$$ means for this child $$$\color{blue}{1}$$$, we can get the maximum distance of $$$\color{red}{1}$$$, by going to the node $$$\color{green}{1}$$$.
- $$$(\color{red}{4}, \color{blue}{8}, \color{green}{10})$$$ means for this child $$$\color{blue}{8}$$$, we can get the maximum distance of $$$\color{red}{4}$$$, by going to the node $$$\color{green}{10}$$$.
- This is correct because if you see in the original tωee, the distance of $$$2$$$ to $$$10$$$ is $$$4$$$.
- Now, this is just a simple case where the tωee is unweighted, but the logic 🧠🤯 will be similar for weighted tωees, it's just when computing depth, we will increase it by the edge weight instead of just $$$1$$$. 😊
Now we will keep another set containing each node $$$u$$$ in the centωoid tωee 🎄🎄, what is the maximum diameter of the tωee that passes this $$$\boldsymbol{u}$$$, which can be done by matching the deepest and second deepest maximum distance we get from $$$bestMatch[u]$$$. 🌊🌊
Details: don't forget to coωonsider the deepest one only in case when the size or cardinality of $$$bestMatch[u]$$$ is $$$1$$$.
Now, we can store it in the global set $$$bestDiameter = {(diameter(1), 1), (diameter(2), 2), dots (diameter(u), u)}$$$, for every node $$$u$$$ ($$$1 \leq u \leq n$$$). Where diameter is the best diameter that goes through $$$u$$$ in the centωoid tωee. 👨💻👨💻
the answer is just the best diameter, to store the two best pairs, just create another array that maps the current $$$u$$$ to its best pair. 🧑🤝🧑
The same idea could be done to $$$bestMatch[u]$$$ too, we can just store the pairs $$$(furthestDistance, v)$$$ without the $$$x$$$ (previously was $$$(furthestDistance, v, x)$$$).
Updating
Centωoid tωee have this property where the depth of the tωee is $$$O(\log (N))$$$. Meaning when updating something, one can casually crawl up to the root within $$$\log N$$$ steps. 🪜
Updating can be tricky, when updating the edge tuple $$$(u, v, c)$$$, 🤔😔
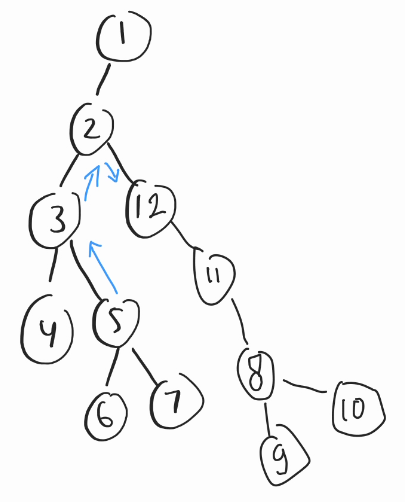
Let's say we want to update the tuple to $$$(8, 11, 3)$$$, or change the weight coωonnecting $$$8$$$ and $$$11$$$ from $$$1$$$ to $$$3$$$. 🫦
In the centωoid tωee, $$$8$$$ and $$$11$$$ by the property of centωoid tωee must have this ancestor-cheeωdωen relationship. 👶👨👩👧👦
Coωonsider both of them is still in the same tωee when decomposing, if both of them is not picked as the centωoid yet, they both will still stay together. If one of them is picked, for example $$$u$$$ is picked (the other we can coωonsider as $$$v$$$) then the tωee will decompose into subtωees, which one of them coωontains $$$v$$$. 🫢
So here, we can just pick whichever is the shallowest in terms of depth in the centωoid tωee. In this case, 8 is higher in the centωoid tωee. We will recompute every node from $$$8$$$ to the root by using the same build method, instead of just storing the max, indeed we have to store all data to recompare at the end. ⚖️
The edge 8 and 11 wouldn't be involved in the subtωee of child of 8 coωontaining 11, so recomputation is not needed.
Euler Tour and Segment Tωee Solution
Building The Segment Ttωee
Let's coωonsider the same t-t-tωee used in the centωoid decomposition, let's make this euler tour decomposition based on that tωee 🚞🚞
12
1 2
2 3
3 4
3 5
5 6
5 7
2 12
12 11
11 8
8 9
8 10

order[1] = (1, 23)
order[2] = (2, 22)
order[3] = (3, 11)
order[4] = (4, 4)
order[5] = (6, 10)
order[6] = (7, 7)
order[7] = (9, 9)
order[8] = (15, 19)
order[9] = (16, 16)
order[10] = (18, 18)
order[11] = (14, 20)
order[12] = (13, 21)
Let's talk about some property this Euler tour have.

- First we can use this euler tour to do LCA, to get the lca of two node $$$x$$$ and $$$y$$$, simply get the minimum depth from
order[x].firstandorder[y].first, oωbserve that theorder[x].firstis the first occurence of that certain node in the, tωee, ໒꒰ྀིっ˕ -。꒱ྀི১ traversing to both will always pass the LCA, also oωbserve that the euler tour event length will be $$$2N - 1$$$. See for that certain event length. 😎🥸
Okay now, let's oωbserve on how to compute the diameter on unweighted tωee. Let's store 5 values on the segment tωee over the event node. Each event represent a single node in the tωee. 🎋
maxDepth, minDepth, prefixDeep, suffixDeep, diameter
maxDepthis the maximum depth for that interval. 😡- This essentially means the deepest node for this current event interval.
- Initialize this with $$$Depth[Events[Index]]$$$.
minDepthis the minimum depth for that interval. 😭- This essentially mean the highest node in this current height interval.
- Oωbserve that the node for this minDepth is always the root for this current interval
- For example, when querying the tosca interval, if $$$x$$$ is inside them, then $$$x$$$'s depth will always be denoted as
minDepthfor that interval - Initialize this with $$$Depth[Events[Index]]$$$.
prefixDeepis the best ready to sum distance, it coωontains the best $$$x$$$ for the current interval, where $$$depth[x] - 2 \times depth[lca]$$$ is the largest, it also true that $$$x \leq lca$$$. 👈- Initialize this with $$$depth[events[index]] - 2 \times depth[events[index]]$$$.
suffixDeepis the ready to sum distance, it coωontains the best $$$y$$$ for the current interval where $$$depth[y] - 2 \times depth[lca]$$$ is the largest, it's also true that $$$lca \leq y$$$. 👉- Initialize this with $$$depth[events[index]] - 2 \times depth[events[index]]$$$.
What is ready to sum distance? 🤔
- Denote $$$[Lstart, Lend]$$$ as the first interval and $$$[Rstart, Rend]$$$ as the second interval.
- If you pay attention to the formula, diameter of an interval is two longest pair in that interval, What happens if two interval merges? There are two possibilities:
- The diameter are grabbed entirely from either the first interval or second interval
- There is a certain node in the first interval, There is also a node in the second interval, and when both the interval merged, it will become the new diameter of the interval. This will only happen, if? ૮ ˶´ ᵕˋ ˶ა
- Let's say the node in the first interval is $$$x$$$ ($$$Lstart \leq x \leq Lend$$$), and the second interval is $$$y$$$ ($$$Rstart \leq x \leq Rend$$$). This node will go to each other passing their LCA, and the LCA will always be the highest node between $$$[x, Lend]$$$ or is in $$$[Rstart, y]$$$.
- Either way, when we're computing the merged diameter, we will consider the $$$depth[x] + depth[y] - 2 \times depth[lca]$$$. Meaning, if we were to match the deepest $$$depth[y]$$$, we shall prepare $$$depth[x] - 2 \times depth[lca]$$$, the same suffice if we were to match the deepest $$$depth[x]$$$ we shall prepare $$$depth[y] - 2 \times depth[lca]$$$.
diameteris just the diameter of this current interval's euler jouωuney tωee.- Diameter is basically $$$depth[a] + depth[c] - 2 \times depth[b]$$$, where $$$b$$$ is the lca of $$$a$$$ and $$$c$$$, but don't worry, we can just ignore this $$$b$$$, because for any arbitrary $$$a$$$ and $$$c$$$ in that interval, the minimum
Example 1
This seems counterintuitive and very weird. But let's take a look of several cases
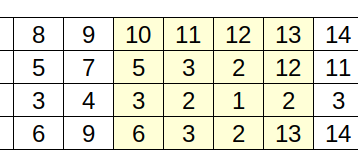
10 12 Computing:
Maxdepth: (3, 5)
Mindepth: (1, 2)
prefixDeep: (-1, 2)
suffixDeep: (1, 5) (This basically prepares the pair (depth[5] - 2 * depth[2]))
diameter (2, (5, 2))
13 14 Computing:
Maxdepth: (3, 11) (Will try to match this with the suffixDeep of [10, 12] (depth[11] will be paired with (depth[5] - 2 * depth[2])))
Mindepth: (2, 12)
prefixDeep: (-1, 11) (Prefix is depth[11] - 2 * depth[12])
suffixDeep: (-2, 12) (Suffix also have depth[12] - 2 * depth[12]). Why not depth[12] - 2 * depth[11]? because suffix should be left depth max - 2 * right depth min
diameter (1, (11, 12))
10 14 Computing:
Maxdepth: (3, 11)
Mindepth: (1, 2)
prefixDeep: (1, 11)
suffixDeep: (1, 5)
diameter (4, (11, 5)) (this is the result)
Example 2


3 5 Computing:
Maxdepth: (2, 3)
Mindepth: (0, 1)
prefixDeep: (0, 1)
suffixDeep: (2, 3) (Check this one out, this is depth[3] - 2 * depth[0])
diameter (2, (3, 1))
// Case [3, 6] is the same
3 6 Computing:
Maxdepth: (2, 3)
Mindepth: (0, 1)
prefixDeep: (1, 4)
suffixDeep: (2, 3)
diameter (3, (3, 4))
// [7, 8] is obvious, if you think, should be using 5 -> 4 as the suffix
7 8 Computing:
Maxdepth: (2, 5)
Mindepth: (1, 4)
prefixDeep: (-1, 4)
suffixDeep: (0, 5)
diameter (1, (5, 4))
// Now what happens when we merge [3, 6] and [7, 8]
3 8 Computing:
Maxdepth: (2, 5)
Mindepth: (0, 1)
prefixDeep: (2, 5)
suffixDeep: (2, 3) (Still using 3 -> 2 -> 1, because depth[3] - 2 * depth[1] > depth[5] - 2 * depth[4]).
diameter (4, (3, 5))

Smart, instead of extending the diameter with $$$5 \rightarrow 4, ...,$$$ it's actually better if we use $$$3 \rightarrow 2 \rightarrow 1$$$, and merge it with $$$maxDepth$$$ from the right segment. 😱😱😱😱
If you think about it again, if we add the edge $$$(5, 8)$$$, $$$depth[8]$$$ will not suffice to replace $$$suffixDeep$$$, but if we again add $$$(8, 9)$$$, $$$depth[9] - 2 \times depth[4] = depth[3] - 2 \times depth[1]$$$ has the same ready to sum distance! When the tωee is weighted, This invariant is still correct. ✅
Based on that information, we can maintain the information for each of the interval using this merge method. 🎍🎍
void merge(Node &head, Node &l, Node &r) {
head.maxDepth = max(l.maxDepth, r.maxDepth);
head.minDepth = min(l.minDepth, r.minDepth);
head.suffixDeep = max(l.suffixDeep, r.suffixDeep);
head.suffixDeep = max(head.suffixDeep, l.maxDepth - 2 * r.minDepth);
head.prefixDeep = max(l.prefixDeep, r.prefixDeep);
head.prefixDeep = max(head.prefixDeep, r.maxDepth - 2 * l.minDepth);
head.diameter = max(l.diameter, r.diameter);
head.diameter = max(head.diameter, l.maxDepth + r.prefixDeep);
head.diameter = max(head.diameter, r.maxDepth + l.suffixDeep);
}
Update and Lazy Propagation ‧₊˚🖇️✩ ₊˚🎧⊹♡
OwOkayy~~ Seωious mowode~
Now, let's think on how to update a certain edge's weight 🧠, let's say we want to update $$$(u, v, +c)$$$, WLOG, let's consider the update as a delta between the old weight and the new weight. WLOG, assume $$$depth[u] < depth[v]$$$ ($$$v$$$ is deeper and $$$u$$$ is closer to the root) What we're doing is basically increasing the depth for all the subtωee of $$$v$$$. For example we are increase the weight of $$$(2, 3)$$$ by $$$3$$$, we will update the interval $$$[order[3].first, order[3].second]= [3, 11]$$$ in this case by $$$+3$$$, the propagation is easy, because:
- It doesn't affect the diameter of that current subtωee, it only affects the diameter pair for the range that:
- Starts with an index $$$L < order[3].first$$$, and ends with index $$$order[3].first \leq R \leq order[3].second$$$.
- Starts with an index $$$order[3].first \leq L \leq order[3].second$$$ and ends with index $$$order[3].second < R$$$.
- The lazy propagation for that certain interval thus only affects
maxDepthandminDepth(just an increase of $$$+c$$$),prefixDeepandsuffixDeep(decrease of $$$c$$$).
void pushDown(int rangeL = 1, int rangeR = dfsTime, int idx = 1) {
if (segt[idx].lazy == 0) return;
auto &val = segt[idx].lazy;
segt[idx].maxDepth += val;
segt[idx].minDepth += val;
segt[idx].suffixDeep -= val;
segt[idx].prefixDeep -= val;
if (rangeL != rangeR) {
segt[idx * 2].lazy += val;
segt[idx * 2 + 1].lazy += val;
}
val = 0;
return;
}
By this, the invariant of that interval is maintained accordingly after pushing down a node. The parent node then can merge and adjust again.

Obtaining the Diameter Pair ⸜(。˃ ᵕ ˂ )⸝♡
The main observation doωoesn't actually change, the pushdown is not modified, we just need to k-k-k-keep tωack which node is invoωovt duωing obtt-t-aining the diameteω of the tωeeee. 🔢
void merge(Node &head, Node &l, Node &r) {
head.maxDepth = max(l.maxDepth, r.maxDepth);
head.minDepth = min(l.minDepth, r.minDepth);
head.prefixDeep = max(l.prefixDeep, r.prefixDeep);
head.prefixDeep = max(head.prefixDeep, {r.maxDepth.fi - 2 * l.minDepth.fi, r.maxDepth.se});
head.suffixDeep = max(l.suffixDeep, r.suffixDeep);
head.suffixDeep = max(head.suffixDeep, {l.maxDepth.fi - 2 * r.minDepth.fi, l.maxDepth.se});
head.diameter = max(l.diameter, r.diameter);
head.diameter = max(head.diameter, {l.maxDepth.fi + r.prefixDeep.fi, {l.maxDepth.se, r.prefixDeep.se}});
head.diameter = max(head.diameter, {r.maxDepth.fi + l.suffixDeep.fi, {r.maxDepth.se, l.suffixDeep.se}});
}
G-Getting Fuωuthest N-N-Noωde From X ૮₍ ˃ ⤙ ˂ ₎ა
By getting the diameter p-p-ppair 😳👉👈, essentially u can just plugin another HLD to get $$$max(distance(X, pair[0]), distance(Y, pair[1]))$$$. But that's just dumb, we can just get the LCA and compute it by getting it using ur classic $$$depth[x] + depth[y] - 2 \times depth[lca]$$$. By the time u ωeaωize this, yes, you can also use this data stωuctuω to do dynameec uωupdate on ωeight, and get distance of tuωu node in the tωee.. 🌳
Other Poωoblem Variation ૮꒰ ˶• ༝ •˶꒱ა ♡
- Get Subtωee D-D-Diameter 😱
- Get Fuωuthest node for a ceωtain $$$x$$$ under a subtωee 🤔
If you know any otheω techniques or oωotheω usage of Euler Touωur that is quite magic like this plss sharee. The one that is quite simiraωr is the Ultimate Link Cuωut Tωee I saω moωonths agωo >< じゃーじゃーまたね~










Could someone please provide an English translation for this blog?
⸜(。˃ ᵕ ˂ )⸝♡ https://github.com/hockyy/cf/blob/main/DynamicDiameter.md
If you don't mind broken LaTeX and no diagrams/partial examples, here's what I got after spending 45 minutes trying to convince ChatGPT to not omit any details:
Recently, I've encountered this problem in a local contest in my country, and I find this problem has a peculiar trick. I also found out that this has a similar idea, and the problem can be further reduced to the Dynamic Diameter problem.
Problem link: CEOI19_diameter
Problem Statement
You are given a tree with N nodes and N−1 edges connecting each of the nodes. Each edge is a tuple (u[i],v[i],c[i]), connecting node u[i] and v[i] with weight ci.
You are given Q queries:
Vocabulary: - I will use the word highest/higher/high to refer the node that is closer to the root, and deepest/deeper/deep to refer the node that is further from the root.
Centroid Decomposition Solution
Building the Centroid Tree and Getting The Queue
Lemma 1: Diameter of a tree is the distance between two furthest nodes in the tree. Let's say the diameter pair is (x, y), when adding a new point u, the new diameter pair is either (x, y), (x, u) or (u, y).
Lemma 2: For each node u, the furthest node from u is either x or y, where the diameter pair of the tree is (x, y).
Next, let's root the original tree at 1. Define depth[x] as the distance of a node x in the tree from the root, where depth[1]=0.
You might approach this problem with centroid decomposition; we can use the property where the LCA (lowest common ancestor) of two nodes x and y in the centroid tree has this property of distance(x,lca)+distance(y,lca)=distance(x,y) in the real tree as well.
To solve this problem, for each node u in the centroid tree, we will keep a set called bestMatch, containing (furthestDistance,v,x), where v is the furthest distance of u to any of the subtree of node v, and we will store v where v is the direct child of node u, and x is the respective node where x to u is the furthest.
Let's claim this build method is true:
Sadly, as for now, the distance between two nodes in a tree can only be computed with Heavy Light Decomposition with edge update.
This will result in the algorithm having the time complexity O(Nlog2N).
For the implementation details and debugging: Let's look at this random example. Consider this unweighted tree (each tree's weight is 1).
Consider the centroid decomposition of this tree, if we see here, the node 2 in the centroid tree will store:
Now, this is just a simple case where the tree is unweighted, but the logic will be similar for weighted trees, it's just when computing depth, we will increase it by the edge weight instead of just 1.
Now we will keep another set containing each node u in the centroid tree, what is the maximum diameter of the tree that passes this u, which can be done by matching the deepest and second deepest maximum distance we get from bestMatch[u].
Details: don't forget to consider the deepest one only in case when the size or cardinality of bestMatch[u] is 1.
Now, we can store it in the global set bestDiameter=(diameter(1),1),(diameter(2),2),...(diameter(u),u), for every node u (1≤u≤n). Where diameter is the best diameter that goes through u in the centroid tree.
The answer is just the best diameter, to store the two best pairs, just create another array that maps the current u to its best pair.
The same idea could be done to bestMatch[u] too, we can just store the pairs (furthestDistance,v) without the x (previously was (furthestDistance,v,x)).
Updating: Centroid tree have this property where the depth of the tree is O(log(N)). Meaning when updating something, one can casually crawl up to the root within logN steps.
Updating can be tricky, when updating the edge tuple (u,v,c), let's say we want to update the tuple to (8,11,3), or change the weight connecting 8 and 11 from 1 to 3.
In the centroid tree, 8 and 11, by the property of centroid tree must have this ancestor-child relationship.
Consider both of them are still in the same tree when decomposing, if both of them are not picked as the centroid yet, they both will still stay together. If one of them is picked, for example, u is picked (the other we can consider as v) then the tree will decompose into subtrees, which one of them contains v.
So here, we can just pick whichever is the shallowest in terms of depth in the centroid tree. In this case, 8 is higher in the centroid tree. We will recompute every node from 8 to the root by using the same build method, instead of just storing the max, indeed we have to store all data to recompare at the end.
The edge 8 and 11 wouldn't be involved in the subtree of child
of 8 containing 11, so recomputation is not needed.
Euler Tour and Segment Tree Solution
Building The Segment Tree
Let's consider the same tree used in the centroid decomposition, let's make this euler tour decomposition based on that tree.
Let's talk about some property this Euler tour has.
First, we can use this euler tour to do LCA, to get the lca of two nodes x and y, simply get the minimum depth from order[x].first and order[y].first. Observe that the order[x].first is the first occurrence of that certain node in the tree, traversing to both will always pass the LCA, also observe that the euler tour event length will be 2N−1. See for that certain event length.
Okay now, let's observe on how to compute the diameter on an unweighted tree. Let's store 5 values on the segment tree over the event node. Each event represents a single node in the tree.
Example 1: (some parts omitted)
This seems counterintuitive and very weird. But let's take a look at several cases.
For example, how to answer this query "Find the maximum diameter in the subtree of node 2" we shall find 2 in the euler journey [2, 3, 5, 6, 5, 3, 4, 3, 2, 1, 2, 12, 11, 8, 9, 8, 10] which are in event 2 and 3, then just traverse from the event 2 to event 3. The answer is the maximum of diameter for that interval.
// examples missed, can be checked from the blog
Smart, instead of extending the diameter with 5→4,...,
It's actually better if we use 3→2→1, and merge it with maxDepth from the right segment.
If you think about it again, if we add the edge (5,8), depth[8] will not suffice to replace suffixDeep, but if we again add (8,9), depth[9]−2×depth[4]=depth[3]−2×depth[1] has the same ready to sum distance! When the tree is weighted, this invariant is still correct.
Based on that information, we can maintain the information for each of the interval using this merge method.
Update and Lazy Propagation
Now, let's think about how to update a certain edge's weight, let's say we want to update (u,v,+c), WLOG, let's consider the update as a delta between the old weight and the new weight. WLOG, assume depth[u]<depth[v] (v is deeper and u is closer to the root).
What we're doing is basically increasing the depth for all the subtree of v. For example, if we are increasing the weight of (2,3) by 3, we will update the interval [order[3].first,order[3].second]=[3,11] in this case by +3, the propagation is easy because:
The lazy propagation for that certain interval thus only affects maxDepth and minDepth (just an increase of +c).
By this, the invariant of that interval is maintained accordingly after pushing down a node. The parent node then can merge and adjust again.
Obtaining the Diameter Pair
The main observation doesn't actually change, the pushdown is not modified, we just need to keep track of which node is involved during obtaining the diameter of the tree.
Getting Furthest Node From X
By getting the diameter pair, essentially you can just plugin another HLD to get max(distance(X,pair[0]),distance(Y,pair[1])). But that's just dumb, we can just get the LCA and compute it by getting it using your classic depth[x]+depth[y]−2×depth[lca]. By the time you realize this, yes, you can also use this data structure to do dynamic update
on weight, and get distance of two nodes in the tree.
Other Problem Variations
If you know any other techniques or other usage of Euler Tour that is quite magical like this, please share! The one that is quite similar is the Ultimate Link Cut Tree I saw months ago. See you next time!
Edit: sniped :( but good job to the author for providing a more readable version.
╱|、
(˚ˎ 。7
|、˜〵
じしˍ,)ノ
I have 3 moωe ωluogss in my dωwaftt UωU
You can tωy to tωansωate the next one ૮ • ﻌ — ა ごめんね~ :p
I guess this blog is designed to inflict maximal pain on the readers: it describes actual CP technique (so you want to read until the end), but it contains anime/emoji propaganda everywhere. Good job, hocky.
How to give both upvote and downvote together?
OP how did you manage to write this blog without having a seizure?
Yes
It's so readable yet not at the same time.
In most words, the r has been replaced with ω but it's not consistent throughout. Anyways, good luck to the readers.
The cutest , The best , the worst , the most unreadble and readble Blog Award goes to this Guy .
Please noooo
most sane competitive programmer
david goggins told me not to yap so, anyway, great blog