Codeforces and Polygon may be unavailable from May 23, 4:00 (UTC) to May 23, 8:00 (UTC) due to technical maintenance. ×

Misa-Misa's blog

Help me with this tree dp problem!!
By Misa-Misa, history, 5 months ago, In English

Given a tree with $$$N$$$ vertices, find the number of rooted trees (which consist of some edges present in the given tree) with $$$K$$$ vertices, including vertex 1. Constraints: $$$1 \leq K \leq N \leq 3000$$$.

Example :
Let $$$N$$$ = $$$5$$$ and the tree be this :

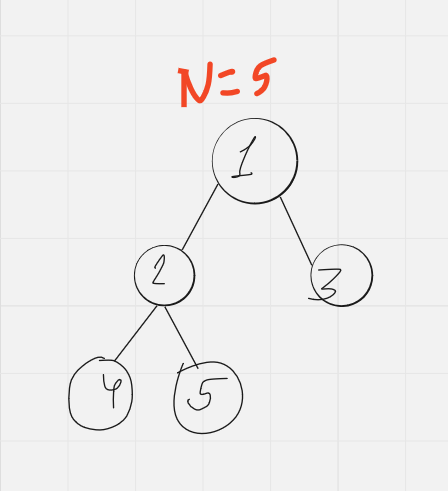
Then for K = 1, 2, 3, 4, 5 the solutions are :

This problem was taken from snuke 's blog

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
5 months ago, # |
← Rev. 2   Vote: I like it -9 Vote: I do not like it

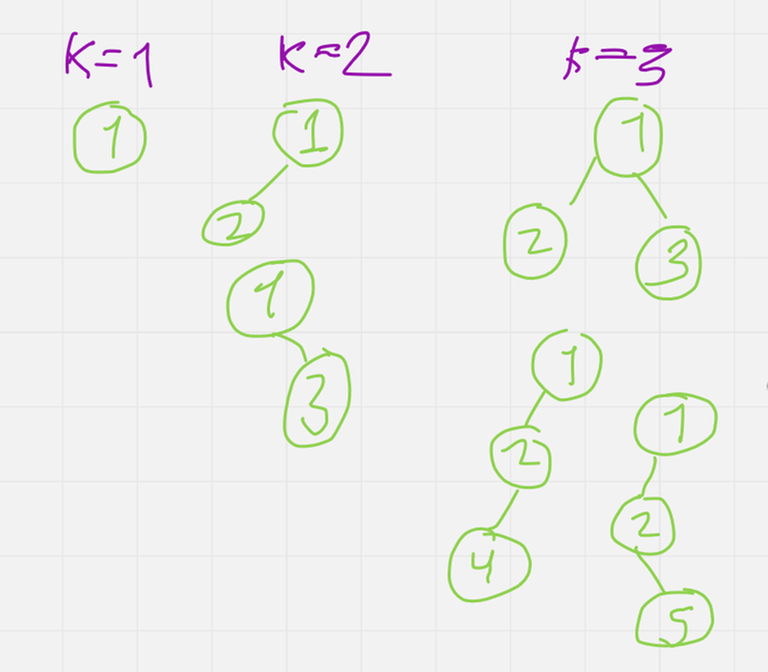
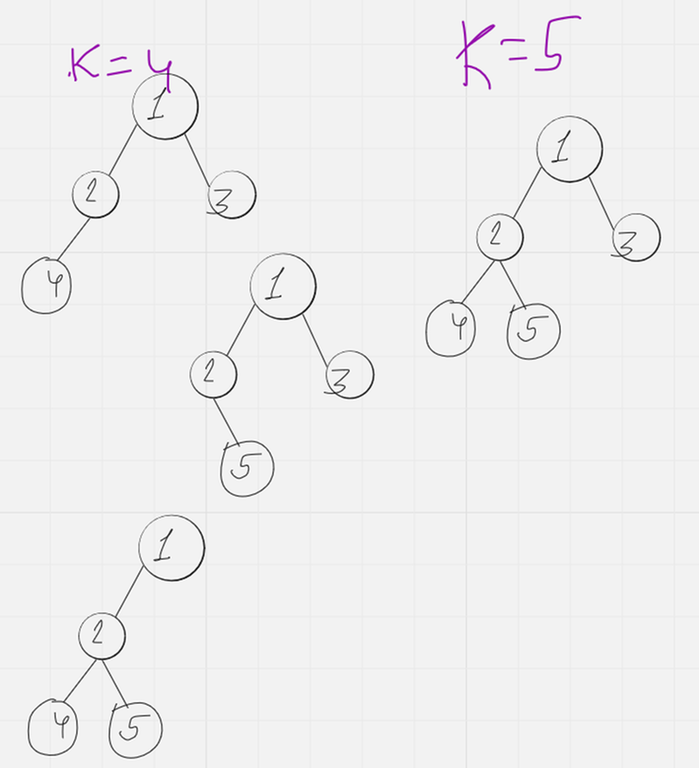
This is probably a knapsack that runs in O(n^2) instead of the O(n^3) you expected. In case you want to overkill it use FFT.

→ Reply