Overview
There are 3 normal tasks accompanied with 2 challenge tasks in div 1 as we usually do. You can check the Statistics by By DmitriyH for detail.
Problem B, C is by sevenkplus, problem D is by xlk and problem A, E is by me.
Problem E is rather complicated then hard, it means if you carefully broke down the problem into smaller ones, it became quite straightforward. During the contest, only kcm1700 managed to solve it successfully.
Problem D, which decided the round boiled down to the following nice Dynamic Programming subproblem: you are given 220 numbers. For each position i between 0 and 220 - 1, and for each distance j between 0 and 20, what is the sum of the numbers with such indexes k that k and i differ in exactly j bits? The fun part is not how to do it T times, it is how to do it even once on 106 numbers.
Petr solve A, B, C, D steadily and fast who indisputably, is the winner of the round. The second place came to msg555, closely followed by cgy4ever. It is worth mentioning that, cgy4ever solved Problem D in the last few seconds which is quite impressive.
Editorial
Problem 2A. Little Pony and Crystal Mine
Brief description:
Draw the grid graph as the problem said.
Analysis:
Just a few basics of your programming language. It's easy.
Problem 2B. Little Pony and Sort by Shift
Brief description:
Ask the minimum unit shift you need to sort a array.
Analysis:
Just a few basics of your programming language. It's not hard.
Problem A. Little Pony and Expected Maximum
Brief description:
Calculate the expected maximum number after tossing a m faces dice n times.
Analysis:
Take m = 6, n = 2 as a instance.
6 6 6 6 6 6
5 5 5 5 5 6
4 4 4 4 5 6
3 3 3 4 5 6
2 2 3 4 5 6
1 2 3 4 5 6
Enumerate the maximum number, the distribution will be a n-dimensional super-cube with m-length-side. Each layer will be a large cube minus a smaller cube. So we have:
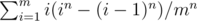
Calculate in may cause overflow, we could move the divisor into the sum and calculate (i / m)n instead.
Problem B. Little Pony and Harmony Chest
Brief description:
You are given sequence ai, find a pairwise coprime sequence bi which minimizes 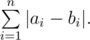
Analysis:
Since {1, 1 ..., 1} is a pairwise coprime sequence, the maximum element of bi can never greater then 2mx - 1. Here mx is the maximum elements in ai. So what we need consider is the first a few prime factors. It is not hard to use bitmask-dp to solve this:
for (int i = 1 ; i <= n ; i ++) {
for (int k = 1 ; k < 60 ; k ++) {
int x = (~fact[k]) & ((1 << 17) - 1);
for (int s = x ; ; s = (s - 1) & x) {
if (dp[i - 1][s] + abs(a[i] - k) < dp[i][s | fact[k]]){
dp[i][s | fact[k]] = dp[i-1][s] + abs(a[i]-k);
}
if (s == 0) break;
}
}
}
Here dp[i][s]: means the first i items of the sequence, and the prime factor have already existed. And fact[k]: means the prime factor set of number k.
Problem C. Little Pony and Summer Sun Celebration
Brief description:
Given a undirected graph with n nodes and the parity of the number of times that each place is visited. Construct a consistent path.
Analysis:
There is no solution if there is more than 1 connected component which have odd node (because we can't move between two component), otherwise it is always solvable.
This fact is not obvious, let's focus on one component. You can select any node to start, denoted it as r (root). Start from r, you can go to any other odd node then back. Each time you can eliminate one odd node. After that, if r itself is odd, you can simply delete the first or last element in your path (it must be r).
The only spot of the above method is the size of the path can been large as O(n2). We need a more local observation. Let's check the following dfs() function:
void dfs(int u = r, int p = -1){
vis[u] = true;
add_to_path(u);
for_each(v in adj[u]) if (!vis[v]){
dfs(v, u);
add_to_path(u);
}
if (odd[u] && p != -1){
add_to_path(p);
add_to_path(u);
}
}
This dfs() maintain the following loop invariant: before we leave a node u, we clear all odd node in the sub-tree rooted at u as well as u itself.
The only u can break the invariant is the root itself. So after dfs(), we use O(1) time to check weather root is still a odd node, if yes, delete the first or last element of the path (it must be r).
After that, all the node will been clear, each node can involve at most 4 items in the path. So the size of the path will less than or equal to 4n. Thus the overall complexity is O(n + m).
Problem D. Little Pony and Elements of Harmony
Brief description:
Given you a vector e and a transformation matrix A. Caculate eAt under modulo p.
Analysis:
Let's consider the e = [1 1 ... 1]. After a period, it will be ke where k is a const. So we know that [1 1, ..., 1] is an eigenvector and k is the corresponding an eigenvalue.
The linear transformation has 2m eigenvectors.
The i(0 ≤ i < 2m)-th
eigenvector is [(-1)^f(0, i) (-1)^f(1, i) ... (-1)^f(2^m-1, i)], where f(x, y) means that the number of ones in the binary notation of x and y.
We notice that the eigenvalue is only related to the number of ones in i, and it is not hard to calc one eigenvalue in O(m) time. To decompose the initial vector to the eigenvectors, we need Fast Walsh–Hadamard transform.
Also check SRM 518 1000 for how to use FWT. http://apps.topcoder.com/wiki/display/tc/SRM+518
In the last step, we need divide n. We can mod (p * n) in the precedure and divide n directly.
Problem E. Little Pony and Lord Tirek
Brief description:
n ponies (from 1 to n) in a line, each pony has:
- si: the start mana.
- mi: the maximum mana.
- ri: mana regeneration per unit time.
Also, you have m operations called Absorb Mana t l r. For each operations, at time t, count how many mana from l to r. After that, reset each pony's mana to 0.
Analysis:
Key Observation
The income of a operation, is only relevant with the previous operation. In other words, what we focus on is the difference time between adjacent operations.
Weaken the problem
Let us assume si = 0 and ri = 1 at the beginning to avoid disrupting when we try to find the main direction of the algorithm. Also it will be much easier if the problem only ask the sum of all query. One of the accepted method is following:
Firstly, for each operation (t, l, r), we split it into a insert event on l, and a delete event r + 1. Secondly, we use scanning from left to right to accumulate the contributions of each pony.
In order to do that, you need a balanced tree to maintenance the difference time between adjacent operations, and a second balanced tree to maintenance some kind of prefixes sum according to those "difference".
The first balanced tree could been implemented by STL::SET. For each operation, you need only constant insert and delete operations on those balanced tree, thus the overall complexity is O(nlogn).
General solution
Instead of scanning, now we use a balanced tree to maintenance the intervals which have same previous operation time and use a functional interval tree to maintenance those ponies. For each operation, we use binary search on the first balanced tree, and query on the second balanced tree. Thus the overall complexity is O(nlog2n).










wow! editorial is available even before system testing is finished! :)
PS: thanks so much, it was a good contest (although i think my rating will decrease). :)
Can you explain me how to solve Div2-B ? I am beginner here.Hope you dont mind.
NOTE: It's possible to solve, iff from any postion (0...N-1) we are able to get a circular ascending array.
1) Find the index with the minimum value, Let it be 'I' then, from there you will have to make N-1 comparitions between 2 adjacent sequences to make sure it satisfies the ascending array property. if possible then answer is 'N — I' else -1. You will have to use MOD N with index
O(logn2)? That should be O(log2n)
P.S. all links to the problem goes to problem 346A. Maybe there are some bugs
Wait ... Let me fixed them ...
Codeforces latex doesn't work properly as handling exponents :
log^2ncannot show log2nBut I think the latter is more of natural. Actually this issue has been discussed in some other posts.
i don't get it
110
this is my hacked solution for DIV2-C with python
I don't really understand this line "Calculate in may cause overflow, we could move the divisor into the sum and calculate (i / m)n instead." can you help me?
n**kcould be VERY VERY VERY large (100000100000) , which surely overflows any type of floating point number; or cause your python solution which automatically turns into BigInteger operations and get TLEIn C/C++ maybe i^n wont fit in a 32/64 bit integer and its less likely that (i/m)^n will overflow so you distribute 1/m^n over the sum.
sorry i clicked it randomly
when i = 1, m = 100000, and n >= 100, then (i/m)^n will become zero.
Can we Solve DIV 2 D using backtracking ? If yes Can anyone explain to me how. I am still confused when it comes to complete search (Backtracking). Maybe if anyone has a good Resource.
Thank yoou :D
Yes of course we can actually this is the way i used , the difference between backtracking and solving is that in backtracking u know the minimum and u just want to print any valid path here is my code for better understanding http://codeforces.com/contest/454/submission/7343464
For C, a more intuitive way of thinking is: if all connected graph has a solution, then if we just focus on any spanning tree, it will also have a solution. And the tree version is very easy.
For D, I was astonished to see the word "eigenvectors" and "Fast Walsh–Hadamard transform". I haven't heard "Fast Walsh–Hadamard transform" before, so I guess that knowledge is too advanced (and seems only dzy493941464 and Jacob solved it by this). Hopefully we can solve it by matrix using symmetry: (00000 -> 00111 by t times) = (00000 -> 10101 by t times) since (00000^00011) and (00000^10101) have same number of 1s.
The fun part is not how to do it T times, it is how to do it even once on 10^6 numbers.
P. S. I have no idea what is FWHT.
Sorry I misunderstand your solution. So our solution seems to be same. :)
I also use your way to to solve the "how to do it even once on 10^6 numbers" part but get TLE. Then I find that code can be optimized to a DP which is only few lines.
problem B and C is nice problem. well done story about Twilight Sparkle....
but : There is no solution if there is more than 1 connected component which have odd node (because we can't move between two component), otherwise it is always solvable.
how to prove it ? i don't understand why?
You must visit at least one node (the node with odd number of visits) in two different components. How do you move from one component to the other? It's impossible by the very definition of component; if it's possible, then both should be merged into one component.
Otherwise, it will always be solvable with the given algorithm in the editorial:
well,i got it. thanks a lot. i'll try to solve it
if we have a graph like 1 - 2 - 3 - ... - n and xi = 1, then won't this approach give more than 4n nodes in the final answer (for large n)?
PS: i read the editorial, but could not understand clearly.
Yes, this approach uses more than 4n vertices. I only responded that it's possible, not possible within 4n vertices.
To do within 4n vertices, the editorial uses some kind of DFS algorithm, although I myself don't quite understand it. So I'll give my approach, which I didn't submit because the code went too messy and I gave up fixing it. (Read: Might be wrong.)
The basic idea is DFS, visiting all vertices in a component, also double-walking some of the vertices if necessary to get the proper parity.
Call an odd vertex to be a vertex visited an odd number of times, and an even vertex similarly.
0, like sample 3.)visited; also keep track of a stackpath_from_rootand a listfinal_path.visited[u]to be true, push u topath_from_root, add u tofinal_path, and recurse.path_from_root; this will be u, and the top item ofpath_from_rootis the "parent" of u, say p. Add p tofinal_path.final_pathin that order.path_from_root. Now you have visited everything in this component with the appropriate parities, except probably the root. If the parity of the root doesn't match, remove the last element fromfinal_path(which will necessarily be the root).-1. Otherwise,final_pathcontains our path.This should find the path with no more than 4n vertices.
It's not always true that 'u is an even vertex' means 'it must be visited one more time'. Why? You're considering visiting this vertex again at the end of DFS routine for this vertex — that's OK. However, by this time you could've visited this vertex both odd and even number of times (it depends on quite many factors).
The easiest way to understand the algorithm is:
That's exactly why I added about toggling the vertex u if a child of u is odd... I think that works, at least.
Or otherwise, let's spam toggles of parities.
First, construct any spanning tree from an odd vertex, and for clarity let's direct all edges away from root. Now we traverse this tree from the root, performing a DFS, visiting every leaf and backtracking up. Every time we visit a vertex, we toggle it, no exception. We also add that vertex to the final path. When we're traversing an edge backward (from v to u), we're leaving v forever; if v is odd after toggling, then we need to visit it one more time, thus add an additional v, u to the final path (and consequently toggle both v and u again).
backward (from v to u), we're leaving v forever; if v is odd after toggling, then we need to visit it one more time, thus add an additional v, u to the final path (and consequently toggle both v and u again).
Yes, that approach gives accepted (with 2ms shy from time limit!). Here's a commented solution, because I code in Python: 7337171
(Or one that is slightly optimized (33ms from time limit), but not commented: 7337040)
I was afraid that 2^16 won't pass in B, so I coded 2^10 * 7, but it costed me much more effort ; /. But in fact those two values are not that far from each other, so probably it is my fault of not properly estimating runtime.
Me, too. Maybe the SIMPLE & FORCE solution is easier to code, haha~
Actually, Problem B of Div 1 can be solved with less time complexity. Considering we may choose primes more than 30 only when they are not multiplied, and only from small to bigger one(a[i]<=30), so we can only store the situation of ten primes less than 30 and use 0..7 to indicate the situation of how the primes more than 30 are used.
E can be solved in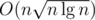 using a sqrt-decomposition. Either way, I failed to code it properly and I don't know whether it fits into TL.
using a sqrt-decomposition. Either way, I failed to code it properly and I don't know whether it fits into TL.
I've coded it on the contest, but it didn't fit into 3 seconds on the 12th pretest. However, I've submitted it less than 3 minutes before the end of the contest, so I didn't even try to optimize it.
Egor also coded it and passed that test, but his solution got runtime error on some further test.
Can someone explain Div2/D with more details?
Firstly the maximum number we can choose is MAXP = ( 2 * mx ) — 1, where mx is a maximum number in array, then the prime numbers to MAXP are 16. For each number we can choose ( from 1 to MAXP ), we store in i-th bit, if i-th prime number exist in his divisors. Now we makе dp, which stores the position in array we have reached and mask, which stores, if i-th prime number is used already ( if i-th bit is one, we cannot use this prime and all numbers, which contain in divisors this prime ). We need to store and a currently selected number, to recover a new array.
I did not get why the maximum chosen number is (2*mx)-1 . Can you please clarify?
If the chosen number c is bigger than (2 * ai) — 1, we can replace that number by 1, the cost is ai — 1, which is less or equal than c — ai, as (2 * ai — 1) — ai = ai — 1
Also, using 1 can allow more available factors for later use, so it is always better
Ok got it . Thanx.
We can choose 1 for all b[i], so we don't need the chose number which is bigger than 2 * x - 1. Take a positive k.(2 * x - 1 + k) - (x) = x - 1 + k — — — (x - 1 + k) > (x - 1)
Can someone please explain Problem A. Little Pony and Expected Maximum in more detail please?
me too, that picture: Take m = 6, n = 2 as a instance.
6 6 6 6 6 6
5 5 5 5 5 6
4 4 4 4 5 6
3 3 3 4 5 6
2 2 3 4 5 6
1 2 3 4 5 6
i think this is m=6 and n=6 too, wtf is this
We compute the number of times i appears as the maximum number among the n rolls.
For i to be maximum, we may not have any number greater than i appearing. In other words, there are in ways to do this; each roll has i possibilities, and there are n rolls.
However, in case none of the rolls gives i, we cannot have i appearing as maximum; it doesn't even appear. Thus we must subtract with the number of cases this happens, which is (i - 1)n for the same reason as above. Thus i appears as maximum in in - (i - 1)n cases.
Now we just use the expected value formula: sum of values over all cases divided by the number of cases. The sum of values can be rephrased as sum of (each value times number of cases); in other words,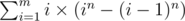 . For each i = 1, 2, ..., m, the value is the maximum, namely i, and the number of cases has been computed above. The total number of cases is clearly mn.
. For each i = 1, 2, ..., m, the value is the maximum, namely i, and the number of cases has been computed above. The total number of cases is clearly mn.
Thus we get the formula: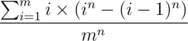 .
.
Now, it's obvious that we will get various overflows; just take i = 100000, n = 100000, and in = 100000100000 = 10500000. Thus we should merge in the denominator to the numerator, producing an easier-to-compute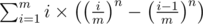 . We get losses of precision, but they don't matter.
. We get losses of precision, but they don't matter.
Many thanks! i wondered why i could not think out of this :D
The final expression (upon simplifying this expression a bit) comes out to be:
Could anyone tell me what is bitmask-dp?
Compress some 0/1 data into a single integer and that's called bitmask. In this problem, we should record "if prime factor x appears". And that's a typical problem which bitmask DP can be used to solve.
Well, thank you!
In Problem B's code,the positions of "{}" of the "for(int s...)" and the blanks in it are not correct, though that is not important.
div1B you just need to use number from 1 to 58. so n can be very large! since there are only 16 primes you can make at most 16 numbers (>1 and any pair of them won't share same prime) so if n>16 ,then you must use (n-16) '1's so the time complexity 16*58*(2^16)+n*log(n)
why we only have 16 primes guys!
because we can use infinitely times of 1. So why use numbers greater than 58? (all input number smaller than 30)
I mean if n<=1000000 it's still solvable
xiaodao said: Problem 2A. Little Pony and Crystal Mine ...
Just a few basics of your programming language. It's easy.
It's not easy for me, I am only a little horse born in 2002.
Sorry, I just lazy...:D
DIV1 B also can be solved using bruteforce with the following observation:
There is no need to use a prime more than 59, so there can't be more than 17 different values in answer, which greater than 1.
We can iterate all possible 2 .. 59 prime compositions, which values are less than 60. There is approx 8M such compositions.
If we sort the input sequence, for each composition we can calculate the answer, using only suffix of input (the greatest values) and partial sum for least values.
7325387
In Div1 B, can you please tell the algorithm to find all the compositions which is relatively comprime?
Recursively, for the current prime x :
- try to skip it
- try to add v = x, v = x*x, v = x*x*x, ... as separate value to composition (v <= 59)
- try to mult v with previous generated values in composition (v * c <= 59)
see CheckAllNumbers function in the provided submission for details.
1.1 sec
what does this line
for (int s = x ; ; s = (s - 1) & x)do? can someone explain?It's a way of iterating over all subsets of x (and skip all non-subsets automatically). s is the current subset, and
(s - 1) & xis the lexicographically greatest subset of x, smaller than s, if s is non-empty.why Div2 and why Div1??
Because there can be people like you. :P
thanks for your ans.I wrote a program and test this.it's right. but i have a problem on how to prove this?can u help me?
Basically, you need to understand what exactly
s-1does: it replaces all the trailing zeros by ones and replaces the last one by zero. As the only one in s is also contained in x, we basically do the same thing with(s-1)&x: remove the last one and replace all trailing zeros from the subset by ones. It's exactly 'taking the previous subset'Would
(s-1)&sdo the same thing as(s-1)&x?Edit: never mind, I see through my own tests that it does not.
I think the Dfs() in Problem C is wrong.
Why can't two components be an answer ? I mean if all the parity bit is zero for all the places. Then nightmare didn't visited any of the places. Isn't this a solution? zero is an even number too.
"There is no solution if there is more than 1 connected component which have odd node (because we can't move between two component), otherwise it is always solvable."
In Problem C. must be
dfs(v, u); add_to_path(**u**);Problem B has gave so much fun time solving it..very nice problem to practice dp with bit masks. Thanks for editorial!
If you want, similar problems : D. Cunning Gena, D. Roman and Numbers
https://codeforces.com/contest/453/submission/226920919
I am trying to solve problem B of div 1 using memoization. Dp function is fine but I am facing issue in printing the answer. I know that the code is wrong as it will update values of ans equal to A[i]. Could you please help me how to update the code to print optimal array chosen by the recursive function
Div1 A can ve solved in O(log n) time instead of O(mlogn) time. First we calculate the results for n=1 and n=2 in O(1) time. Lets call the result for n=1 F1 and n=2 F2 ... The formula is: Fi=-0.5*F(i-2)+1.5*F(i-1) With this formula we can calculate Fn in log n time
Did you test it out? It seems to be incorrect :(
I can't understand div1 E'solution clearly. How to ues functional interval tree ? How to use a balanced tree ? I need help。
No wonder you cannot understand the solution, it is rather poorly explained.
There are two separate problems here:
For a given interval [p,q], how to find (=iterate over) all intervals with the same previous operation. Clearly, after you find and process those intervals, you erase them (as you have to add operation on [p,q], which covers them). It can be done by storing all intervals in a set and using lower_bound/upper_bound function to find intervals covered by [p,q]. For more details check out this comment.
How to process one interval, which has the same previous operation*. You have to answer the following query: "how much mana will the given interval [p,q] regenerate over the period of t units?". We can do the following. Build a counting tree-like structure, where every node is responsible for some subsegment of ponies. You can preprocess this subsegment by finding all moments, where some pony reaches its maximum. So in t=0 no pony has reached maximum, in t1 first one, in t2 second one etc. In addition to that, for each ti precompute how much mana those "maximized" ponies posess and how much mana is regenerated by the rest of the ponies. It is linear (both in time an memory)**, but if you sum all the lengths of the intervals in the tree, you will see it is nlogn, so we're fine:) Having this structure, you query a segment [p,q] in the same way as a standard counting tree.
If you don't believe me, check out 7320365
ad* if there is no previous operation on a given interval, just bruteforce it! You will do it once per pony only :)
ad** in fact, it is O(klogk) time and it should be enough, but you can do it linearly by merging two child nodes.
I hope I helped :)
I don't understand the tutorial of div1 D(Little Pony and Elements of Harmony). Is there anybody who is kind enough to teach me what is going on?
Please In A. Little Pony and Expected Maximum, I wrote a solution and submitted it but give wrong answer for expected value = 4.4336 and my output = 4.43369. But when I tested this test case on Idone.com it gave me the exact correct value of 4.4336 not 4.43369?!! Why this .00009 appears when I run my solution here?
Where is your code? Can you give me the link here?
Your output is 4.43269, not 4.43369.
i noticed u copied this part from Petr's weekly round-up! :D
At least it is grammar safe ...
pseudocode for dfs in problem C is wrong. here is the corrected one:
it's important to notice that add_to_path(x) also does
odd[x] = !odd[x].Thank you ... fixed.
I read all the comments regarding Div2/D problem above and understood a little beat. But I am not getting the meaning of 0/1 here. for e.g what is meaning of this string "1111 1111 1111 0101" (in binary) here? Plz someone clarify it more.
This is a bitmask .. you can think it as a bool[]。 Each bit represent weather a prime factor is exist or not.
Problem A. Little Pony and Expected Maximum:
Suppose I have m faced dice.I know that i th face came maximum with i^n-(i-1)^n occurence. I prove it with a different idea using combinatrics and binomial coefficent.
In div 1/B little pony and harmony the result for the below two implementations are different can someone explain.
Second implementation gives correct answer whereas the first one gives wrong result.
1 << 17 — 1 is not equal to (1 << 17) — 1
Ignore this comment. I found my mistake :)
Anybody has a good enough time complexity for the DP bitmasks solution in B. Little Pony and Harmony Chest. Looking at the 3 loops then one may come up with a complexity $$$\approx n * 60 * 2^{16} = 393216000 \approx 4e8$$$ which quite hard to fit in the time limit!
Thanks for reading my question. <3 <3
I tested the code above (count how many times the 3 loops are) and it turned out to be $$$\approx 3e8$$$ for $$$n = 100$$$. So nevermind answering my question above :D.
Also check SRM 518 1000 for how to use FWT. http://apps.topcoder.com/wiki/display/tc/SRM+518
This link is not working anymore, if possible someone can provide a working link?
I used binomial expansion formula to derive the formula in the editorial of Little Pony and Expected Maximum
Alternate $$$O((q + 10^5).\sqrt{n} + n\log{n})$$$ solution for div-1 E, using square root decomposition:
1) Divide pony array into square root blocks. Now notice that, whenever a pony's mana is reset, it reaches its maximum mana in not more than $$$1e5$$$ seconds. So now precompute, for each block $$$B$$$ and for all $$$t$$$ from $$$1$$$ to $$$1e5$$$, the amount of total mana all ponies in block $$$B$$$ will have if all of them were reset $$$t$$$ seconds ago. This can easily be done in $$$O((10 ^ 5).\sqrt{n})$$$.
2) We also need to store some additional information, for all blocks and that is:
3) Now when answering queries, you can just brute force for the blocks which dont lie completely in query range as usual. What about the blocks which lie completely inside the query range? For all blocks in which all ponies were last reset at same time, we can just use the precomputed value. For the blocks in which all ponies were not last reset at the same time, we can brute force for this entire block. It is easy to show that the second kind of blocks will occur no more than $$$2q$$$ times, because such blocks are created at edges of query ranges.
Note: Take care of the ponies with $$$0$$$ regeneration rate.
Implementation: link
https://codeforces.com/contest/453/submission/226920919
I am trying to solve problem B of div 1 using memoization. Dp function is fine but I am facing issue in printing the answer. I know that the code is wrong as it will update values of ans equal to A[i]. Someone please help me how to update the code to print optimal array chosen by the recursive function