At this problem you need to model what written in statements. Also, it can be proved, that answer can be calculated using formula: 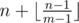 , where ⌊ x⌋ is the integer part of x.
, where ⌊ x⌋ is the integer part of x.
460B - Little Dima and Equation
Obviously S(x) can take only integer values and 1 ≤ S(x) ≤ 81. Let's check S(x) from 1 to 81, and calculate B * S(x)A + C. After that if sum of digits of this number is equal to S(x), it is positive and less than 109, than it is a solution.
There could be bug because of using C++ pow() function.
Note,that answer is positive integer not greater than 109 + 105. Using binary search on answer, we will find answer. Really, we can check in O(n) if some height is achievable. We go from left to right. For current flower we calculate how much times it need to be watered to stand not lower than checking value. If cuurent flower need to be watered for h times, we will star h segments in current flower. We would keep array, in which st[i] — number of segments, which starts in i-th flower. Also, we will keep variable, in which we will keep number of segments, which cover current flower. This variable could be updated at O(1). Really, to get new value we just need to subtract st[i - w], and, if we create new segments, to add st[i]
Also, it can be proved that simple greedy algorithm works. At every of m iterations we can find the leftmost flower with the smallest height and water the segment, which begins in it. Primitive realisation works at O(nm), so you need to use data structure, which can add on segment and find minimum at segment. For example, you can use segment tree with lazy updation or sqrt-decomposition. Such solutions works longer, but faster than TL
Prove: Consider any optimal sequence of moves (using which max. answer reachs). Consider initially the leftmost smallest flower, and suppose all segments which covers it.(suppose, there are at least 1 segment, because else answer is initial height of this flower, so we can put a segment to start in this flower, and answer would not change). Suppose that there are no segments, which starts from current flower. Consider the rightests of segments.(If there are more than one, than any of them). Than, we can move this segment to start in the initially leftmost smallest flower, and the answer would not change. Really, flowers, which earlier was at this segments were higher, than leftmost smallest, and were watered not least times. So, after we moved the answer had not decreased. So, new sequence is also optimal. So, there is sequence of moves, which consists the segment, which starts at the initially leftmost smallest flower. So, let use this. Similary to other of m days, and it would be optimally. 7536171
If r - l ≤ 4 we can all subsets of size not greater than k. Else, if k = 1, obviously that answer is l. If k = 2, answer is 1, because xor of numbers 2x and 2x + 1 equls 1. If k ≥ 4 answer is 0 because xor of to pairs with xor 1 is 0.
If k = 3, we can choose numbers 2x and 2x + 1 with xor 1. So we need to know, if we can get xor equals 0. Suppose that there are 3 such numbers x, y and z (r ≥ x > y > z ≥ l) with xor equals 0. Consider the most non-zero bit of number x. At the same bit of y it's also 1, because xor equls 0, and y > z. Consider the next bit of numbers. If z have 0 there, we have to do next: set the previous bit of numbers x and y equals 0, and set current bit equals 1. Obviously xor still equals 0, z hadn't changed and numbers x and y stood closer to z, so they are still at [l, r].And x > y.Consider the next bit of numbers. If z has zero here than we will change most bits of x и y at the same way and so on. z > 0, so somewhen we will get to bit in which z has 1. Since xor equals 0, the same bit of x would be 1 because x > y, and y would have 0 there. At the next bits we will change bit in x to 0, and in numbers y and z to 1.Finally z would be greater or equal than before, and x would be less or greater than before, and x > y > z would be correct. So, we have the next: if such numbers x, y and z exist than also exist numbers:
1100…000
1011…111
0111…111
with xor equals 0. There are not much such triples, so we can check them.
Formal statement: 2 natural numbers are given: R — radii, and N — number of points. You have to choose N unnesessarily distinct points A1, A2, ...AN which are lying inside or on side of circle, such that
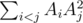
takes its maximal value.
At first let 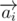 be a vector from (0, 0) to point Ai. Value of
be a vector from (0, 0) to point Ai. Value of 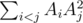 is equal
is equal 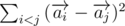 , what is equal to
, what is equal to 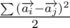 , and it can be rewritten as
, and it can be rewritten as 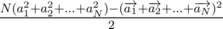 . It makes us think that it is more profitable take point which are close to circle, such that |ai2| would be as big as can, but value of
. It makes us think that it is more profitable take point which are close to circle, such that |ai2| would be as big as can, but value of 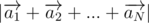 as little as can. After that it becomes obvious, that if N is even, than it's enough to take any diameter and place half of points to the start and another half to the finish of it. Now we're trying to formulate our guessians strictly. Let's take an optimal set of points. Let's mark coordinats as (x1, y1), (x2, y2), ..., (xn, yn).Let's first N - 1 points are fixed, and we can move last point — (x, y). In terms of x, y we'd like to maximize
as little as can. After that it becomes obvious, that if N is even, than it's enough to take any diameter and place half of points to the start and another half to the finish of it. Now we're trying to formulate our guessians strictly. Let's take an optimal set of points. Let's mark coordinats as (x1, y1), (x2, y2), ..., (xn, yn).Let's first N - 1 points are fixed, and we can move last point — (x, y). In terms of x, y we'd like to maximize
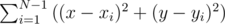
We left out all squares without x, y. Maximization of this x, y function is equivalent to maximization of
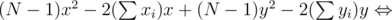
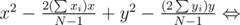
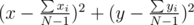
So, we've reduced our problem to finding the furthest integer point from 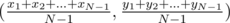 . Now we can declare: the furthest point is placed at one vertex of convex hull of all integer points inside the circle.
. Now we can declare: the furthest point is placed at one vertex of convex hull of all integer points inside the circle.
Proof. Let 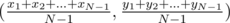 be a point T, and the furthest integer point inside P (convex hull) is X(obviously, it placed somewhere in convex hull). Lets extend TX beyond X to intersection with one side of polygon — let it be AB, and lets mark point of intersection as X'. Clearly TX' ≥ TX. It's easy to see, that one of angles
be a point T, and the furthest integer point inside P (convex hull) is X(obviously, it placed somewhere in convex hull). Lets extend TX beyond X to intersection with one side of polygon — let it be AB, and lets mark point of intersection as X'. Clearly TX' ≥ TX. It's easy to see, that one of angles 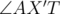 and
and 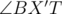 is obtuse, so, according to properties of obtuse triangles on of inequalities holds: TA ≥ TX' ≥ TX or TB ≥ TX' ≥ TX, so, we can replace X to A or B, and distanse TX will increase.
is obtuse, so, according to properties of obtuse triangles on of inequalities holds: TA ≥ TX' ≥ TX or TB ≥ TX' ≥ TX, so, we can replace X to A or B, and distanse TX will increase.
So, we can assume, that every point in optimal set belongs to the convex hull. So, solution is check all sets of points from convex hull and check values on this sets. If R ≤ 30, then convex hull contains no more than 36 points — it's easy to check with computer. So, brute force will take 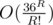 time, and it passes TL easily (depending on realizations and optimizations).
time, and it passes TL easily (depending on realizations and optimizations).
For those, who interested in realization of algorithm: at first we place convex hull to some vector(and points become ordered). After that we build recursion function with the next parameters:1) how many points in the set on this iteration 2) vector with points 3) sum x-coordinats of points from set 4) sum of squares of x- coordinates 5) sum of y-coordinates 6) sum of squares of y-coordinates.
On each iteration we take last point from set, and trying to add all points, starting with this, and finishing on the end of convex hull — it starts new iteration of recursion. Also, we recalculate meaning of cur value in fast way using parameters 3, 4, 5 and 6.
On the last iteration, when we took N points, we are comparing value on this set with maximal value. If maximal value is less, than cur value, then maxvalue = curvalue, and bestvector = cursetofpoints. After recursion we output maxvalue and bestvector.
UPD Editorial of problem C was expanded











Limit is 10^9.. checking till digit sum 72 -_-
I'll not forget this round!
10^9 has 10 digits, which means that the highest reachable number can be 999999999; S(999999999)=81.
Same mistake!! Became Green as a result!! HOW!
same mistake TT
done same and got hacked
Wow, very fast editorial. Thanks for it!
coded the same algo as written in Problem B
but was unaware of the issue with C++ pow() and hence became newbie :/
You learn from your mistakes. Be glad that it's only an online competition. I lost a national olympiad silver medal because pow(10,2) gave me 99, but I knew what to do now. :)
can someone please explain what does the check() function actually check for/how it works, in the referred submission of Problem C
http://codeforces.com/contest/460/submission/7536171
I also couldn't understand the check() function,do you make it??
yeah I got most of it.. see the updated editorial for problem C
I'm curious about the greedy solution for C. When we find the leftmost smallest element (let's name it L), do we always water flowers [L, L+W] (except when you can't go right anymore)?
Suppose you're going from left to right, and the current position is i. This means that all flowers before i have already been watered enough. Now if the flower at position i is too short, then we conclude that we need to water it x times, and that there is no point in watering the flowers to the left -- it does not improve the answer. So the only choice left is to water the [i, i + w) segment x times.
Could you help me debug this submission 7543565? It seems that I have an infinite loop in my binary search (test case 20), but I can't seem to find it.
The complexity is O(nw), so I doubt the approach is wrong (although I admit it could be optimised).
O(nw) (with a hidden constant factor due to the binary search) is too slow for this problem, because the statement says 1 ≤ w ≤ n ≤ 105.
You need a faster way to do range updates. Some people used a segment tree for this, and some other maintained the current added height and an array of where and how many watered segments end.
Yes. Think like this. You start with the first from the left: if its high is more or equal to the solution you're trying, then there is no problem and you continue to the next one; if high is less than the solution, then you have to water that flower (solution-high)times and, of course, you water also the flowers to the right (because the ones to the left are already ok).
Hope this helps :)
C++ pow() functions bug ? Could someone explain this for me please ?
The default pow() from the C++ STL (the one in <math.h>) returns a double, not an integer.
By using a double you are prone to rounding errors (if you are not aware why, research on how are doubles stored), which can sometimes offset a whole number when casting to integer (2.9999999999 can be cast to 2), which can give you a wrong result.
These rounding errors might seem rare, but in ~100 test case at least one is sure to produce it. This is why you should use your own pow function instead, something like :
This will return an integer, making sure you don't get a rounding error.
I think it is if( b== 0) return 1;
Should have been a 1 there, fixed it now.
can anyone explain 460C?? I am unable to get the question?? for the first test case 2 2 2 1 1 1 after 1st day 2 2 2 3 2 2 why din he water for 2nd day so that it would result in 2 2 2 4 3 3 so that 3 is the maximum height of the smallest flower i.e., 1 at the beginning
2 2 2 4 3 3 the maximum height of the smallest flower is 2. it does not mean the height of the smallest flower in the 1st day, but in the m-th day.
Great contest!
Till now I could not believe that my simple back — tracking solution passed E (shocked when looking at the editorial).
The main idea of our solution is to prove, that optimal rearragement of points lies on the convex hull and brute-force it. Could you explain your solution?
In the contest, when I saw n <= 8, I think that may be brute-force works. I tried to implement a slow brute-force consider all points in the circle and realize that there is a 'pattern': if n is even, then we only need points of types (0; r) and (0; -r), else with odd n, it is sufficient to use the points which have maximum distance from O (there are 8 points which have that property), plus 2 points (0; r), (0; -r), we get 10 points in total. So a back-tracking algorithm to deal with these 10 points is enough ! (Actually in my solution, I use up to 27 points, just to ensure the correctness). It seems that the solution described in the editorial uses the same idea as mine, but it need to check all points on the convex hull. Anyway, these are only guesses, I cannot prove it yet.
In the problem c, Can anyone please explain the 2nd technique to solve the problme?
I solved the problem using Sqrt-Decomposition.
What you basically do is that, break the array into sqrt(n) groups of about sqrt(n) elements. Read Here( I read it after translating to English via Google Translate ) Then for each group, you store the minimum element in an array(of size sqrt(n)), with its index.[ Complexity: O(n) ]
Repeat this process m times-> - Find the minimum element in the new array(of size sqrt(n)).[ Complexity: O(sqrt(n)) ] - Then for the minimum element in the whole array, you update the indexes from i (of the min element) to min(i+w-1,n-1) by +1. The process of updation is explained quite well in the article above.
After this process, find the minimum element in the sqrt(n) sized array, and thats your answer.
Overall Complexity: O(m*sqrt(n)) 7558102
I'm new to this concept, but I liked it a lot. All those familiar with Sqrt-decomposition, pls give me some tips as to when and where to apply this concept.
isn't sqrt decomposition just like a worse version of segment tree..
In Problem C, what exactly is "sqrt-decomposition" method?
link
Can anybody explain why the segment tree approach would be correct? I got the idea during the contest but I wasn't sure whether the idea is correct. How can we justify that approach?
what is sqrt-decomposition? I have searched it but founf nothing? could someone tell me? in Chinese if can? thx
In English
Thx!
fast tutorial. great!
Can someone please help me? According to codeforces my solution for Prob 2 fails pretest 8 but on my PC as well as ideone, it works and gives the required output!! here is my solution solution in ideone
You forgot to initialize the variable
suminsum(). And you assign the result of the formula computation tolong int, but it may requirelong long.In addition to andreyv' remarks: You don't check that your answers are in the allowed range. From the problem statement: "Print only integer solutions that are larger than zero and strictly less than 10 ^ 9."
Hi, I solved 460A correctly but i would like to understand the more elegant and mathematical solution posted by this editorial. Can anyone explain why n + [(n-1)/m-1] is the formula ?
We can use mathematical induction on this. Suppose that by having n pairs of socks, Vasya receives a pairs of new socks and lasts for b more days since his last gift; thus Vasya lasts for am + b days.
Now, if we increment n by 1, we can ignore this extra pair of socks and let Vasya to get a pairs of socks and survive for b more days. Now we introduce our new pair of socks. If b ≠ m - 1, then our new pair of socks don't give Vasya any extra pair of socks; just one more day of surviving. On the other hand, if b = m - 1, then after using these socks, Vasya will get another pair, so this increments a and sets b = 1.
Now observe that b goes 1, 2, 3, ..., m - 1, 1, 2, 3, ..., m - 1, 1, 2, 3, ... in a cycle, so we can be sure that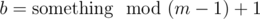 , since it is a repeating sequence of increasing integers of period m - 1, and it begins with 1. By a little trial and error, we get
, since it is a repeating sequence of increasing integers of period m - 1, and it begins with 1. By a little trial and error, we get 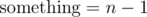 , so
, so 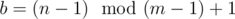 .
.
What about a? It begins at 0, and increases when n = m, 2m - 1, 3m - 2, ...; exactly when b = 1 (except for the first time where n = 1). Thus we need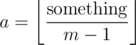 , so that we have a jump every m - 1 steps. Turns out that
, so that we have a jump every m - 1 steps. Turns out that 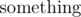 is n - 1, since we need
is n - 1, since we need 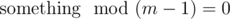 in order for the floor to increase.
in order for the floor to increase.
Now we have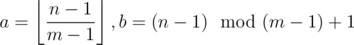 , we plug these into our formula:
, we plug these into our formula: 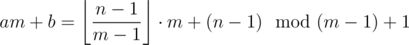 . Ouch, this will be messy.
. Ouch, this will be messy.
Let's split m = (m - 1) + 1. Then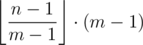 is simply the largest multiple of m - 1 not exceeding n - 1, and
is simply the largest multiple of m - 1 not exceeding n - 1, and 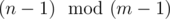 will add for the remainder, so we have
will add for the remainder, so we have 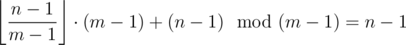 , exactly. Hey, this isn't bad! Adding the + 1 remaining, we get n, the first term of the sequence.
, exactly. Hey, this isn't bad! Adding the + 1 remaining, we get n, the first term of the sequence.
We are left with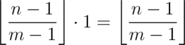 , which is just the second term of what we want to prove. So Vasya survives for exactly
, which is just the second term of what we want to prove. So Vasya survives for exactly 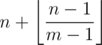 days with his socks, and he really needs to start doing laundry with his possibly 199 pairs of used socks present.
days with his socks, and he really needs to start doing laundry with his possibly 199 pairs of used socks present.
One can also solve E without any insights whatsoever ;)
By rewriting the formula you get that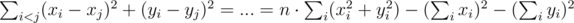 . Notice that we were able to get rid of all double sums. This gives rise to the following dynamic programming solution:
. Notice that we were able to get rid of all double sums. This gives rise to the following dynamic programming solution: 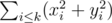 that you can get if you select k points such that
that you can get if you select k points such that 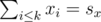 and
and 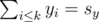 . The complexity is
. The complexity is 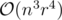 . This is too slow to pass, but you can precompute all the answers locally.
. This is too slow to pass, but you can precompute all the answers locally.
dp[k][sx][sy]is the maximum value of the sumYou can probably also prove that only border points are worth looking at. In this case, one step becomes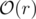 rather than
rather than 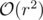 and you don't need precomputations.
and you don't need precomputations.
Anyway, this proves that there is a solution polynomial in n and r, rather than exponential as in the editorial.
You can take a look at my solution: 7529095.
How do you prove that only border points are worth looking at ?
I think they prove it above (in the editorial).
Consider a point that can be moved left or right: (x, y), added as the last one. Its addition incurs an increase in the answer of
while for addition of points (x + 1, y) and (x - 1, y), the increases are
If neither of these points gives a better answer, then V + , V - ≤ V, so
but combining these inequalities together yields 2(n - 1) ≤ 0, which is only possible for n = 1 (which we knew already — if there's just 1 point, it doesn't matter where we put it). Proof by contradiction complete.
I don't know what happens, but for problem E ,The solution run in my machine for about 8 sec. But in codeforces it's 373ms . Is codeforces that fast ? I am using intel core-i-5 with 4 GB ram. Here is my submission 7552805 . You can check it. and the authors solution takes 9 sec. So , CF is 9 times faster than my PC.
Did you compile without -O2 locally?
Problem C: Can anyone explain in more details how to find in O(n) if a fixed height is reachable? I didn't really get it. Thank you!
Iterate the input array from left to right. if you visit a flower with the height less than your fixed height, begin some watering from there, and continue. Now when you check the height of flower, consider your watering before (I call that Y), and add Y to current flower's height.
Because of each watering ends at some position, just subtract the amount of watering that start at position i-w from Y. So it's better to store st[j] which means the amount of watering you start at jth position.
I tried hard, but could not get how this while loop works to find 3 numbers whose XOR is 0, in sample solution for Problem D
Could someone please explain??
Link here: 7536186
See here. Basically you're generating numbers in the form 2·2i - 1, 3·2i - 1, 3·2i, which can be shown to have XOR of 0.
Hi can anybody explain why the segment tree approach would be correct in problem C? I cannot understand why that is the solution?
I have a question about 460E — Roland and Rose My deduction of the formula(and oops I think its right) ∑(ai−aj)/2 = N(a12+a22+....+aN2)−(a1+a2+a3+....+aN)2 (i != j) Does it have some problem?
Maybe you meant ∑(ai − aj) ^ 2 / 2 (i != j)?
In this case you can add to the left part ∑(ai − aj) ^ 2 / 2 = 0 (i == j), because (ai — ai) ^ 2 / 2 = 0.
why the value of |a1+a2+a3...+an| make no difference of the value of(a1^2+....an^2) in problem E?It difficult for me to prove it
Anyone mind proving how n+(n-1)/(m-1) (int n,m) is the correct answer?
Some one please check 11514761 it gives the right answer on ideone but wrong on codeforces?
pow function..got it!
Editorial was probably translated using Google Translator. All we have to do in problem D , Case K = 3 is maintain 3 Numbers Low , Mid , High initially {1,2,3} . Then at any point multiply all by 2 and add 1 to the lowest number(We want lowest number to increase faster and highest number to increase slower and maintain xor 0 so Mid's bit = 1)
hi there,can anyone please explain the editorial of div2 C using binary search approach?? i can't understand the following lines of the editorial :- "If cuurent flower need to be watered for h times, we will star h segments in current flower. We would keep array, in which st[i] — number of segments, which starts in i-th flower. Also, we will keep variable, in which we will keep number of segments, which cover current flower. This variable could be updated at O(1). Really, to get new value we just need to subtract st[i - w], and, if we create new segments, to add st[i]."
You binary search for the maximum height possible for the lowest flower. And you validate the 'mid' of your binary search greedily. This is how you do it. Suppose you are at position i of the array. You already know how many times you have watered the w-length segments starting at each of 1,2,3..i-1 (you have stored these somewhere, i.e. ops[] in my code linked below). Then some of these already-watered segments will affect index i too, more specifically the segments which start at i-w+1, i-w+2,..i-1. Sum up the number of operations on these segments (let it be S). If current_height_of_i + S >= mid, then you don't need to do anything and you can move on to i+1. Else, you need to fill the deficit by watering the w-segment starting at i.
You can look at my code for reference. Hope that helps! :)
thank u... :3
For Vasya and Socks, a simple solution and code.
https://medium.com/@deeptechtalker/vasya-and-socks-codeforces-solution-460a-with-explanation-b4a5aa56c24b
can you explain why we took mod? I mean i get the problem that we were having where the last sock wasn't getting counted(like in 10,2 example). But why mod for that? Bear with me i'm a newbie :)
mod returns the remainder of the integer division, the of the link is based in a integer division n/m, however n is not necessary divisible by m, so the remainder of the disivion is unitized in the iteration, and if its value is unitized we should pass this value to the nexts iterations, because it can contribute to the other iterations.
Something like having the case 5 3, in the first iteration we have $$$5/3 = 1$$$, but with the remainder, in the next iteration n=3=1+2(the mod), so we can divide n again per m in the second iteration, having the answer 7, if we dont use the remainder the code will have just 1 iteration instead of 2.
Thank you for the editorial. The explanation for problem B is obvious.