Hello everyone, I hope you can enjoy this special round for Zepto Lab. Here are the solutions of this round.
A. King of Thieves
This task is easy for many of you. We can just iterate over all possible i1 and i2 - i1, then we can compute i3, ..., 5, and check whether this subsequence satisfies the condition mentioned in the task.
B. Om Nom and Dark Park
We use greedy and recursion to solve this task. For each tree rooted at v, we adjust its two subtrees at first, using recursion. Then we increase one edge from v's child to v.
C. Om Nom and Candies
If there is a kind of candy which weighs greater than 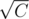 , then we can iterate over the number of it to buy, which is less than
, then we can iterate over the number of it to buy, which is less than 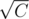 .
.
Otherwise, without loss of generality we suppose 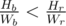 . If the number of the blue candies that Om Nom eats is more than Wr, he could eat Wb red candies instead of Wr blue candies, because Hb × Wr < Wb × Hr. It means the number of the blue candies will be less than
. If the number of the blue candies that Om Nom eats is more than Wr, he could eat Wb red candies instead of Wr blue candies, because Hb × Wr < Wb × Hr. It means the number of the blue candies will be less than 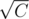 , and we can iterate over this number.
, and we can iterate over this number.
D. Om Nom and Necklace
This task is to determine whether a string is in the form of ABABA... ABA for each prefixes of a given string S
For a prefix P, let's split it into some blocks, just like P = SSSS... SSSST, which T is a prefix of S. Obviously, if we use KMP algorithm, we can do it in linear time, and the length of S will be minimal. There are only two cases : T = S, T ≠ S.
- T = S. When T = S, P = SSS... S. Assume that S appears R times. Consider "ABABAB....ABABA", the last A must be a suffix of P, and it must be like SS... S, so A will be like SS... SS, and so will B. By greedy algorithm, the length of A will be minimal, so it will be SSS... S, where S appears
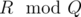 times. And B will be SSS... S, where S appears
times. And B will be SSS... S, where S appears 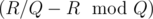 times. So we just need to check whether
times. So we just need to check whether 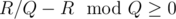 .
. - T ≠ S . When T ≠ S, the strategy is similar to T = S. A will be like "SS...ST", and its length will be minimal. At last we just need to check whether
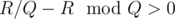 .
.
The total time complexity is O(n).
E. Transmitting Levels
Our task is to compute at least how many number of blocks are needed to partition a circular sequence into blocks whose sum is less than K.
By monotonicity, it is easy to get the length of maximal blocks which starts from 1 to n in O(n). Assume the block with minimal length is A and its length is T, it is obvious that whatever the blocks are, there must be a block that it starts in A. So, we can iterate over all the T numbers of A, making it the start of a block, and calculate the number of blocks.
Notice that all the lengths of blocks is (non-strictly) greater than T, therefore the number of blocks we need is at most N / T + 1. We need to iterate T times, but each time we can get the answer in O(N / T), so finally we can check whether the answer is legal in T * O(N / T) = O(N).
F. Pudding Monsters
Actually this problem is to compute how many segments in a permutation forms a permutation of successive integers.
We use divide and conquer to solve this problem.
If we want to compute the answer for an interval [1, n], we divide this interval into two smaller ones [1, m], [m + 1, n] where 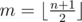 . We only care about the segments which crosses m. We call the first interval L and the latter one R.
. We only care about the segments which crosses m. We call the first interval L and the latter one R.
Considering the positiions of maximum numbers and minimum numbers in these valid segments, There are four possible cases:
- the maximum number is in L, the the minimum is also in L;
- the maximum number is in R, the the minimum is also in R;
- the maximum number is in L, the the minimum is in R;
- the maximum number is in R, the the minimum is in L;
Let A be the given sequence and we define Lmaxp = maxp ≤ i ≤ mAi. Similarly we can define Rmaxp, Rminp, Lminp.
For simplicity we only cares about case 1 and case 4.
In Case 1, we iterate over the start position of the segment, so we know the maximum and minimum number so we can compute the length of the segment and check the corresponding segment using Rmin and Rmax.
In Case 4, we iterate over the start position again, denoted as x. Suppose the right end is y, then we know that Lminx < Rminy, Lmaxx < Rmaxy so we can limit y into some range. Another constraint for y is that Rmaxy - Lminx = y - x, i.e. Rmaxy - y = Lminx - x. Note that when x varies, the valid range for y also varies, but the range is monotone, so we can maintain how many times a number appears in linear time.
It's easy to show that this algorithm runs for  , by Master Theorem.
, by Master Theorem.
There are some other people using segment trees. You can see a nice implement here
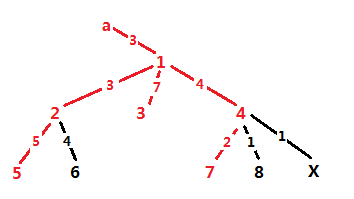
G. Spiders Evil Plan
In this task, we are given a tree and many queries. In each query, we are supposed to calculate the maximum total length of y paths with the constraint that x must be covered.
Consider S is the union of the paths (it contains nodes and edges).
For each query (x, y), if y > 1 , then there is always a method that S is connected.
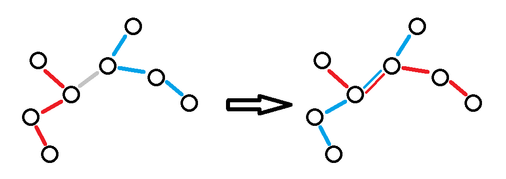
Further, we could get the following theorem:
For an unrooted tree, if it has 2k leaves, then k paths can cover this tree completely.
Proof for this theorem is that, if some edge u - v is not covered, we can interchange two paths, i.e. we change two paths a - b and c - d to a - c and b - d, for a - b in the subtree of u and c - d in the subtree of v.
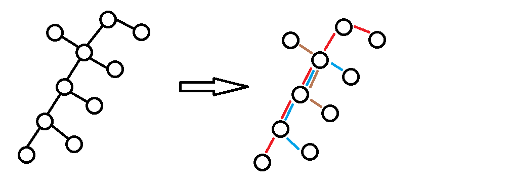
So a query (x, y) could be described as :
Find 2y leaves in the tree, with node x in S, and maximize the total of weight of the edges in S.
For a query (x, y), we can make x the root. Then this task is how to choose the leaves. Note that we could select leaves one by one, every time we select the leaf which makes answer larger without selecting the others, as follow :
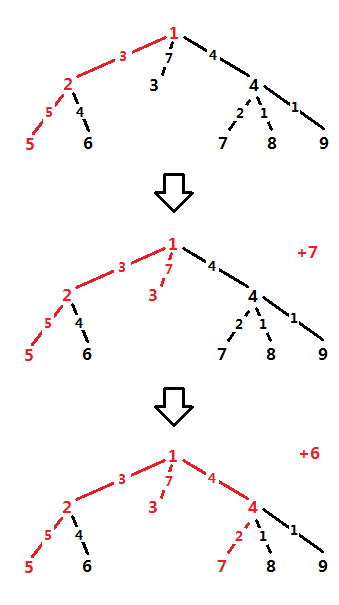
But if for every query we need to change the root, the time complexity cannot be accepted. Assuming the longest path in the tree is (a, b) , we could find that whatever the query is, S will contain either a or b certainly.
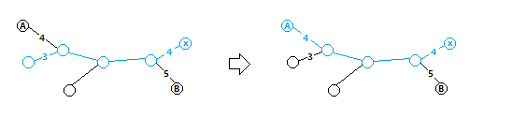
So, we just need to make a and b the root in turn, and get the maximum answers. However, there is another problem : x may not be in S. Like this :
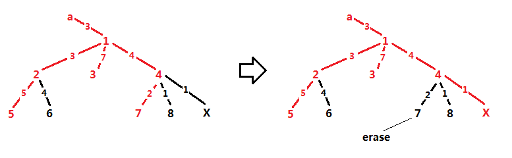
But it doesn't matter. We just need to link x with the selected, and erase some leaf. Of course after erasing, the answer should be maximum.
Thanks, for all of your excellent performance!










thanks for fast editorial :)
Elegant starts with E, which is the perfect adjective for problem E. Awesome problem! :D
What does
Smean for C?Fixed. S should be C
SO SAD!!! Problem C's answer was just 2 simple loop! :(
A very hard problem can easily have a one-loop solution. The main objective is to get it :)
But a very good problem shouldn't because you can guess it accidentally.
Please elaborate the editorial solution for Problem B.
If possible, can someone please explain tourist's solution — 10576165 ?
He is doing the same "DFS", just non-recursively. Imagine that you've walked nearly all the way and there are last two edges in front of you. In order to give them the same sum they must be equal and they don't depend on previous edges. So you can make edges the same in all pairs in the lowest layer, than just add numbers on lowest edges to their parents and "eliminate" the lowest layer (you don't need it anymore). And so tourist is doing.
Here is my solution that is doing exactly the same as tourist's: 10579416, two cycles are just for better understanding of layers idea, it all works in O(N). One-cycle version: 10595439.
Problem C: "If there is a kind of candy which weighs greater than sqrt(C)...." Why happens this special case? Can anyone explain it to me? :S
Suppose that there is a kind of candy which weighs more than sqrt(C), and for better explication suppose this is the red candy, and QR, WR , QB, WB are the quantities and weights of the candies, respectively red and blue. You must satisfy this:
And you want to find QR and QB. But we know that: WR > sqrt(C), so if you multiply by sqrt(C) in each side you maintain the inequality and get this: WR * sqrt(C) > C so if you use sqrt(C) or more red candies you will not satisfy the condition I. , no matter how many blue candies you use. Then QR must be less than sqrt(C), so you only need to iterate from 0 to sqrt(C) to find QR.
Thx a lot.Finally I know.
Thank you! :D
WOW !! That was really good explanation ... Didnt understand a single thing reading the editorial ... but you broke it down very nicely ... thnx man :) mras
Thanks!! :D
what about the case where both WR and WB are less than sqrt(C)?
In problem D, how this string
abaabaabaabaabaacan be divided to A+B+A+B+A (since k=2)?
abaa+ba+abaa+ba+abaa
Thanks.
Problem C
Please explain the editorial when wr and wb is less the sqrt(c).
'If there is a kind of candy which weighs greater than sqrt(C), then we can iterate over the number of it to buy, which is less than sqrt(C).'
Assume that wb > sqrt(C), the maximum number of blue candies that can be eaten is floor(C / wb), which is less than sqrt(C).
We can also say, since wb > sqrt(C), then wb * sqrt(C) > C. Therefore, Om Nom can eat at most sqrt(C) blue candies.
We iterate over the number of blue candies and get all possible answers, then get the largest one of them.
I think the situation he said is WR and WB are less than sqrt(c).And what you talk about is one candy is larger than sqrt(c) :).
Oh sorry... I made a mistake.
When neither of Wb and Wr is larger than sqrt(C), we can assume that Hb × Wr <= Wb × Hr. (If not, swap them.)
As the editorial says, 'If the number of the blue candies that Om Nom eats is more than Wr, he could eat Wb red candies instead of Wr blue candies, because Hb × Wr < Wb × Hr.'
If Om Nom eats Wr blue candies, which weigh Wr × Wb in all, he gets Wr × Hb joy units.
However, if he eats Wb red candies, which also weigh Wr × Wb in all, he gets Wb × Hr joy units.
Since Hb × Wr <= Wb × Hr, the choice of Wb red candies is never worse than Wr blue candies.
Therefore Om Nom should never eat more than Wr blue candies. We iterate over the number of blue candies eaten (which is always less than Wr < sqrt(C)), and find the best answer.
In fact I did't figure it out,but now I do. You really help me a lot.
Wow. It would be really nice to be able to help other people ;)
WOWWWW !! that was really very nice explanation. I got the case for first part, where one of the weight is greater sqrt(C) from mras's comment ... and now i have understood the full solution of it. thanks a lot :) @cyand1317
i don't understand why they've written such short and unclear editorial :( The editorial above for problem C should be replaced with your (cyand1317) and mras's comment :/
I don't understand the C's solution , can any one clarify it more please
cntr and cntb are the answer.
cntr * wr + cntb * wb ≤ c
if cntb > wr then cntb = wr + x and cntr * wr + wr * wb + x * wb ≤ c, so we can take wb red candies instead of wr blue ones, since wr * hb < wb * hr we will get more joy units — which is contradiction, thus cntb ≤ wr.
I may have posted it in wrong place (sorry, it was my first comment), but you can take a look here http://codeforces.com/blog/entry/17281#comment-220872
Can someone explain better the approach with KMP for D?
What does "Q" mean for problem D?
Q means K, you need to make AB block as long as you can
s= SSSS.....ST/ (S as small as posible and T is a prefix of S)
len(AB) = (total S blocks in string s)/K
len(A) = (total S blocks in string s)%K + len(T)
then just check if you have len(AB) >= len(A)
Thank you! finally I got the idea.
I just would add that:
len(AB) = (total S blocks in string s)/K * len(S)
(where len(S) is length of block S in chars)
len(A) = (total S blocks in string s)%K * len(S) + len(T)
There is another solution of problem C:
Obviously, it's impossible that the total weight of red candies is more than
lcm(Wr, Wh)and simultaneously the total weight of blue candies is more thanlcm(Wr, Wh). Because, lets suppose thatlcm / Wr * Hr > lcm / Wb * Hb, we can reduce the amount of blue candies and add some red that the total weight remains the same but this new answer is greater than the last one. So after that we need just to fill the rest weight --max(0, C % lcm + lcm). ButC % lcm + lcm < 2 * lcmand if two nubers havelcm = xthen it means that one of this numbers is greater or equal thansqrt(x). So that means that we need just to iterate over a multiplier ofmax(Wr, Wb)to fill the rest (we need to iterate only overmax(C, 2 * lcm)values).I really can't understand in problem C the case If there is a kind of candy which weighs less than sqrt(C) !! :(
Let's assume both Wr and Wb are less than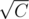 .
.
Assume Wr × Hb < Wb × Hr is satisfied (otherwise we can just swap the candy's color).
Then consider case where we take Wr blue candy. This means we eat Wr × Wb grams candy with joyfulness Wr × Hb. However, we can take Wb red candy instead, because it still weights Wr × Wb grams, with better joyfulness (remember Wr × Hb < Wb × Hr). So whenever we eat more than Wr blue candy, we can always exchange Wr blue candy into Wb red candy for optimality.
Because of that, the number of blue candy taken in the optimal solution will always less than Wr. We can brute force this, which runs in O(Wr). Remember that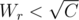 , so we can also say this works in
, so we can also say this works in 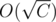 . Really greedy solution :)
. Really greedy solution :)
I got it ! thank you so much
We need to iterate over
min(C, 2*lcm)/Wmaxvalues, and final complexity isO(min(C/Wmax, Wmin)), i.e. lcm/Wmax is Wmin in the bad case.Yes, you are absolutely right. But
O(min(C/Wmax, Wmin))is stillO(sqrt(C)).Hi everyone, I hope someone help me please.
I'm doing the problem D with hash and my solution give WA15, Is this test AntiHash?
I change the alphabet and test with some base too, in every judge give me WA15
This my solution
Indeed.
As a general rule, don't use polynomial hashes modulo a power of two. While it's faster this way, a well-known regular sequence (Thue-Morse) is known to break such hashing.
Here is your solution using hash modulo a prime 1016 + 61, accepted now.
Thanks Gassa, I didn't kwow about the anti-hash tests.
But I dont understand your function mul(a,b,m) when I convert from HASH to long double and multiply two long doubles, Don't lose precision?
Maybe you can explain your function mul :).
(There's a link in the solution, however it goes to the Russian part of Codeforces.)
Let Q (quotient) and R (remainder) be such that a·b = Q·m + R, with 0 ≤ R < m. Our solution will first
(1)find an approximate quotient q, then(2)a value r which differs from the real remainder R by k·m for some small integer k, and finally(3), the real remainder R.At first, we do
Now, q is an approximate quotient (k = |Q - q| is small).
Next,
Here, we try to define r so that a·b = q·m + r. It would follow that r = R + (Q - q)·m.
Actually though,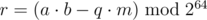 , since the calculations take place in a 64-bit integer. If however the value |Q - q| was so small that |a·b - q·m| < 263, then the above statement r = R + (Q - q)·m is true, and we can then calculate the real remainder by taking
, since the calculations take place in a 64-bit integer. If however the value |Q - q| was so small that |a·b - q·m| < 263, then the above statement r = R + (Q - q)·m is true, and we can then calculate the real remainder by taking 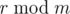 .
.
Here, note that
r % mcan be negative, and we often want the remainder in the mathematical sense (0 ≤ r < m). So, we assume |Q - q| ≤ 5, and so r + 5·m ≥ 0.When the
long doubletype is available, it has the same 64 bits of precision asint64_t, so the approximate quotient q is almost exact. Empirically, |Q - q| is at most 1 for numbers up to 262.A version working for integers up to 262·1.41 is discussed here (in Russian again).
Can someone please explain the solution for problem E? I didn't understand it from the Editorial.
"For a prefix P, let's split it into some blocks, just like P = SSSS... SSSST, which T is a prefix of S. Obviously, if we use KMP algorithm, we can do it in linear time, and the length of S will be minimal" Could anybody explain, how do this using KMP algorithm?
What does "For a prefix P, let's split it into some blocks, just like P = SSSS... SSSST, which T is a prefix of S" means? Can anyone show it on some examples?
Let's look at an example: 'abcabcabcab'
We use KMP algorithm to find the
pre[]array in O(n) time.Obviously, for P =
beads[0..10], our program should get S = 'abc' and T = 'ab'.And for P =
beads[0..5], it should get S = 'abc' and T = 'abc'.In both samples T is a prefix of S (they may be equal).
We know that in the first example, S =
beads[0..2]('abc') and T =beads[9..10]=beads[0..1]('ab').In the second sample S = T =
beads[0..2]('abc').Then through observing we know that S =
beads[0..idx - pre[idx]]and T =beads[0..idx % (idx - pre[idx] + 1)].After finding out the lengths of S and T (their exact values don't matter), we can calculate how many times they appeared in P and then follow the instructions in the editorial to find the answer.
Thank you. Good explanation)
Glad to be helpful =u=
Oh, I forgot a point. After finding S and T we can let A = T and B = S-T, and SSS...SST = ABABA...BA. Therefore if the sequence SSS...SST does exist for P =
beads[0..i](see the editorial), the answer at positioniis '1'. Otherwise, it's '0'. By iterating through the value ofiwe solve the problem in O(n) time.Found bug
Thanks for the skillful E!
For problem D: Could anyone explain why KMP can divide the original string into SSSSS...SST?
Gotcha. A great problem
Hey, can you explain, I still can't figure it out.Thanks
I solved F using divide & conquer (same as editorial), but I still have no idea how it could be solved using Segment tree (like tourist did). Can anyone give some idea? Thanks :)
For each prefix, we will count number of permutation suffixes. While iterating from left to right, imagine we are at the i th index.
valj = max([j..i]) - min([j..i]) + (i - j)
Its obvious that subsequence [j..i] is a permutation if and only if valj = 0.
Also notice that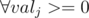 .
.
We can update each valj while iterating from left to right using two monotone queues,(one for minimum and one for maximum). Every change of minimum and maximum can be handled with interval increasing queries.
We will use segment tree to apply those queries and asking for number of 0. Because number of zeros is our interest.
At each segment tree node we need to store 2 integers : minimum value, number of elements under this subtree with minimum value.
If minimum of segment tree's root is more then 0 then number of j's where valj = 0 is also zero. Also that minimum value can not be less then 0, because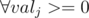 .
.
Thanks! This solution is very amazing :)
Problem B in golfscript(click run to execute).
Test 14 as example.
http://goo.gl/zwMv93
In problem E:
How should I understand this sentence?
Consider the second query in the sample test, the length of maximal blocks start at 1, 2, 3, 4, 5, 6 are 1, 1, 2, 2, 1, 2, respectively. So one of shortest block starts at 1 with length 1. However, making 1 as start of a block costs 5 blocks, when the optimal solution is 4.
Do I misunderstand anything here?
In your example, if you starts with the 2nd block (with length 1), the result is 4. I think what roosephu meant is that there exist a solution, which starts with a block having shortest length (not all configurations, which starts from minimum block result in optimal solution).
I have no idea how to prove this though, it looks so magical.
If so, we have to iterate over ALL shortest blocks, not ONLY ONE, don't we? In this situation, the time complexity should be O(N2 / T) instead of O(T * N / T) = O(N), right?
Yes, we have to iterate over ALL shortest block. But no, the complexity is O(N): There are O(N / T) shortest block, and for each iteration, we need O(T).
Really??? How to do everything in O(T) for each block??? We need to find the number of blocks needed when starting in each shortest block, needn't we?
As I understand this example indeed shows that the above claim from the editorial is wrong, but that's actually kind of special case, when the whole block A (using notation from the editorial) is a suffix of some block from the optimal solution.
So, we should actually try (T + 1) possible start positions — T positions inside the block A and farthest k, such that the block starting from k entirely covers block A.
It's sufficient to consider one point right after the shortest block in addition. Then any solution will have a block starting in one of these T+1 points. Proof: otherwise all T+1 points are contained in a single block; it means that their sum is <= b, and hence the block T could be extended — a contradiction.
Hi there, being curious here, for your example N = 6 right? what about k? under no circumstances your lengths array can be [1,1,2,2,1,2] for that input, since k must be >= to the max value into the array.
Letting that beside, I followed the tutorial, and I didn't have to check every minimal length block, just one, preserving O(N).
This last fact (using only one minimal block) doesn't seems obvious at all to me, can somebody educate me on this aspect. Best regards.
An alternative explanation to D: Let z[i] be the maximum size of a substring starting at i that is also a prefix. (array z is generated by z-algorithm in O(n), find it here) Let string s be the concatenation of A and B. The maximum size of s is O(n/k). For every possible size of s, we need to check if the next k blocks of size |s| are equal. This is equivalent to checking for(p = 0;;p+=|s|) if z[p]>=|s|. If so, let's look at position p = |s|*k in the string. We know that the answer is 1 for the interval [p-1,p+z[p]-1]. (We can choose the length of A arbitrarily, if |A| is 0 then p-1 works and then we can increase |A| while it still is a prefix.) Now that we have all the possible intervals, let's sort them and iterate through position i to see if it is inside any interval. Complexity: The checking can be done in O(k) for every |s|. Since maximum |s| is O(n/k) the total cost O(n/k * k) = O(n). We also need to sort the intervals.
Is there any solution with O(1) complexity for 526C - Om Nom and Candies?
So there is no such solution? Disappointed :/
норм
Problem tag for problem c says it can be solved using ternary search. Has anyone solved it using ternary search?
I still can't understand Problem C ,what's the meaning of "If the number of the blue candies that Om Nom eats is more than Wr, he could eat Wb red candies instead of Wr blue candies, because Hb × Wr < Wb × Hr" ,if he eats Wb red candies,maybe the total weights he eats becomes larger .So maybe he will eat less other candies. So how to prove it's the best solution? Thank you.
Wb red candies have the same total weight as Wr blue candies, namely Wb*Wr.
I got it,thank you !!!
HI, every one! I'd like to ask for you help. For problem D: First, I figure out the pre pointer by using KMP. Second, for each prefix S, check if len(S) % (len(S)*m-pre[len(S)*m-1]) == 0, then use binary searching find the maximum length of T(the prefix of S), that makes S*K+T meets the requirement.
But it WA on the test 16. Could anyone help me find the bug? here is my code: http://codeforces.com/contest/526/submission/10636215
Thank you!
Am I the only one who thinks some parts of this editorial is poorly written? I have to second guess many things to understand what the author really wants to present. For example, if you read the editorial for D:
I am confused, too.
Here's my attempt to give a better explanation of problem E after reading the confusing editorial.
The key observation is: Suppose you know the largest l such that a1 + a2 + ... + al ≤ b. Then the optimal answer must be such that we either we have to take exactly these l numbers in a single pack or we split this segment into two parts {a1, ..., ai} and {ai + 1, ..., al}, and they become the suffix and prefix of some other packings respectively.
Note that we don't split it into three parts. Let's assume we can get better solution if we do so, i.e. there are three packings:
we can rearrange the packing so that it still becomes three valid packings:
This splits the {a1, ..., al} packing into two, but gives the same solution, so it's a contradiction.
To prove the original claim, it's intuitive too. Assume we don't do "keep or split into two" strategy, there must be a packing of the form
But as we assumed, we cannot add more elements outside a1, ...al, so another contradiction.
This implies that you can try all l possible splittings, which implies that for the i-th splitting, start at i-th element, and greedily pack the elements. How fast can this be? Suppose we know that, given b, how far we can pack when we start at the i-th element for all i. Let's denote them as li. Then you just need to know how many "jumps" you need to perform from the i-th position to pack all numbers.
If we know min{li} = l * , it is guaranteed that it takes at most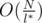 jumps to compute the answer. Back to our original splitting strategy, as we try l different splittings, it takes
jumps to compute the answer. Back to our original splitting strategy, as we try l different splittings, it takes 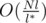 to find the optimal solution. The problem is, l ≥ l * , it could be as slow as
to find the optimal solution. The problem is, l ≥ l * , it could be as slow as 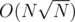 where
where 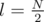 and
and 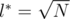 . If l = l * , the algorithm becomes O(N). To do this, note that by rotating {ai} the observation still holds, so one can just rotate {ai} until l1 = l * , and you can get solve it in O(N).
. If l = l * , the algorithm becomes O(N). To do this, note that by rotating {ai} the observation still holds, so one can just rotate {ai} until l1 = l * , and you can get solve it in O(N).
To construct the killer case I described above, consider the following sequence:
Try N = 1000000, b = 500000. It becomes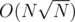 if you don't rotate the first 500000 1s to the left.
if you don't rotate the first 500000 1s to the left.
Can any one explain solution of tourist of problem D(Om Nom and Necklace).
U also c it? scr1, scr2.
yup! i see that too :O why?
For anyone having trouble in reading problem C's editorial, the black strips are all $$$\sqrt{C}$$$.